What Is The Greatest Common Factor Of 8 And 6
pinupcasinoyukle
Nov 23, 2025 · 11 min read
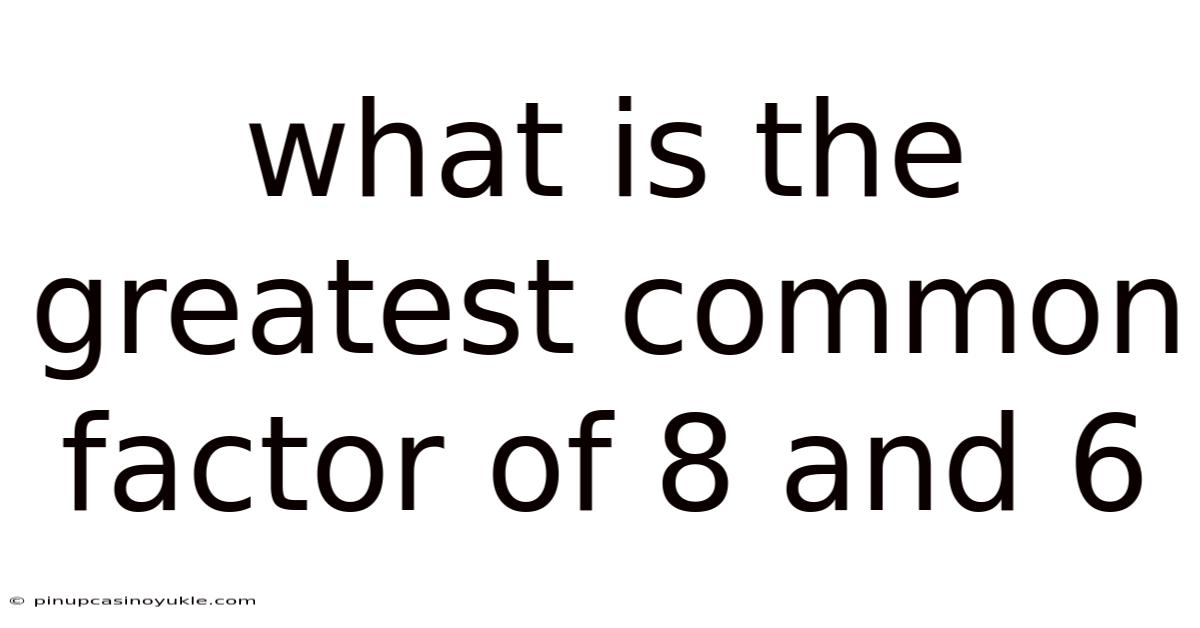
Table of Contents
The greatest common factor, often abbreviated as GCF, is a foundational concept in number theory that helps simplify fractions, solve algebraic problems, and understand divisibility rules. For the numbers 8 and 6, the greatest common factor is the largest number that divides both 8 and 6 without leaving a remainder. This article will explore the concept of GCF, methods to find it, the mathematical principles behind it, practical applications, and frequently asked questions.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the highest common factor (HCF), is the largest positive integer that divides two or more integers without any remainder. It is a critical concept in mathematics, particularly in number theory, arithmetic, and algebra. The GCF is used to simplify fractions, solve equations, and understand divisibility.
Definition and Basic Concepts
The GCF of two or more numbers is the largest number that is a factor of all the given numbers. A factor of a number is an integer that divides the number evenly, leaving no remainder.
Importance of GCF
Understanding and finding the GCF is crucial for several reasons:
- Simplifying Fractions: GCF is used to reduce fractions to their simplest form, making them easier to work with.
- Solving Algebraic Problems: GCF helps in factoring expressions and solving equations.
- Divisibility Rules: Understanding GCF enhances the comprehension of divisibility rules and number properties.
- Real-World Applications: GCF has practical applications in fields like scheduling, resource allocation, and cryptography.
Methods to Find the GCF of 8 and 6
Several methods can be used to find the GCF of two or more numbers. We will explore three common methods: listing factors, prime factorization, and the Euclidean algorithm.
Method 1: Listing Factors
The listing factors method involves identifying all the factors of each number and then finding the largest factor they have in common.
Steps to List Factors:
- List all factors of each number.
- Identify common factors.
- Determine the largest common factor.
Applying the Listing Factors Method to 8 and 6:
- Factors of 8: 1, 2, 4, 8
- Factors of 6: 1, 2, 3, 6
- Common Factors: 1, 2
- Greatest Common Factor: 2
Therefore, the GCF of 8 and 6 is 2.
Method 2: Prime Factorization
The prime factorization method involves expressing each number as a product of its prime factors. The GCF is then found by multiplying the common prime factors raised to the lowest power they appear in either factorization.
Steps for Prime Factorization:
- Find the prime factorization of each number.
- Identify common prime factors.
- Multiply the common prime factors with the lowest exponent.
Applying the Prime Factorization Method to 8 and 6:
- Prime Factorization of 8: 2 x 2 x 2 = 2^3
- Prime Factorization of 6: 2 x 3 = 2^1 x 3^1
- Common Prime Factors: 2
- Lowest Exponent of Common Prime Factors: 2^1
Therefore, the GCF of 8 and 6 is 2.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers using division. This method involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder until the remainder is zero. The last non-zero remainder is the GCF.
Steps for Euclidean Algorithm:
- Divide the larger number by the smaller number.
- Replace the larger number with the remainder.
- Repeat the process until the remainder is zero.
- The last non-zero remainder is the GCF.
Applying the Euclidean Algorithm to 8 and 6:
- Divide 8 by 6:
- 8 ÷ 6 = 1 remainder 2
- Replace 8 with 2:
- Now, we find the GCF of 6 and 2.
- Divide 6 by 2:
- 6 ÷ 2 = 3 remainder 0
- The last non-zero remainder is 2.
Therefore, the GCF of 8 and 6 is 2.
Step-by-Step Calculation and Explanation
To solidify understanding, let's go through each method step-by-step with detailed explanations.
Listing Factors Method:
- List Factors of 8:
- Factors are numbers that divide 8 without leaving a remainder.
- 1 divides 8 (8 ÷ 1 = 8)
- 2 divides 8 (8 ÷ 2 = 4)
- 4 divides 8 (8 ÷ 4 = 2)
- 8 divides 8 (8 ÷ 8 = 1)
- Factors of 8: 1, 2, 4, 8
- List Factors of 6:
- Factors are numbers that divide 6 without leaving a remainder.
- 1 divides 6 (6 ÷ 1 = 6)
- 2 divides 6 (6 ÷ 2 = 3)
- 3 divides 6 (6 ÷ 3 = 2)
- 6 divides 6 (6 ÷ 6 = 1)
- Factors of 6: 1, 2, 3, 6
- Identify Common Factors:
- Compare the lists of factors for 8 and 6 to find the numbers that appear in both lists.
- Common factors of 8 and 6: 1, 2
- Determine the Greatest Common Factor:
- From the list of common factors, identify the largest number.
- The largest common factor of 8 and 6 is 2.
Therefore, using the listing factors method, the GCF of 8 and 6 is 2.
Prime Factorization Method:
- Prime Factorization of 8:
- Prime factorization involves breaking down a number into its prime factors. Prime factors are prime numbers that multiply together to give the original number.
- 8 = 2 x 4
- 4 = 2 x 2
- So, 8 = 2 x 2 x 2 = 2^3
- Prime Factorization of 6:
- 6 = 2 x 3
- 2 and 3 are both prime numbers.
- So, 6 = 2 x 3 = 2^1 x 3^1
- Identify Common Prime Factors:
- Compare the prime factorizations of 8 and 6 to find the prime factors that appear in both factorizations.
- The common prime factor of 8 (2^3) and 6 (2^1 x 3^1) is 2.
- Multiply the Common Prime Factors with the Lowest Exponent:
- Identify the lowest exponent of the common prime factor 2.
- The exponent of 2 in the prime factorization of 8 is 3 (2^3).
- The exponent of 2 in the prime factorization of 6 is 1 (2^1).
- The lowest exponent is 1.
- Multiply the common prime factor 2 raised to the lowest exponent 1: 2^1 = 2
Therefore, using the prime factorization method, the GCF of 8 and 6 is 2.
Euclidean Algorithm:
- Divide 8 by 6:
- Divide the larger number (8) by the smaller number (6).
- 8 ÷ 6 = 1 remainder 2
- Replace 8 with 2:
- Replace the larger number (8) with the remainder (2).
- Now, find the GCF of 6 and 2.
- Divide 6 by 2:
- Divide 6 by 2.
- 6 ÷ 2 = 3 remainder 0
- The Last Non-Zero Remainder is 2:
- Since the remainder is now 0, the last non-zero remainder is the GCF.
- The last non-zero remainder was 2.
Therefore, using the Euclidean algorithm, the GCF of 8 and 6 is 2.
Mathematical Principles Behind GCF
Understanding the mathematical principles behind GCF involves exploring concepts like divisibility, prime numbers, and the fundamental theorem of arithmetic.
Divisibility and Factors
Divisibility is the property of one number being divisible by another without leaving a remainder. A factor of a number is an integer that divides the number evenly. Understanding factors and divisibility is fundamental to finding the GCF.
Prime Numbers and Prime Factorization
A prime number is a number greater than 1 that has no positive divisors other than 1 and itself (e.g., 2, 3, 5, 7, 11). Prime factorization is the process of expressing a number as a product of its prime factors. This concept is crucial in the prime factorization method for finding the GCF.
Fundamental Theorem of Arithmetic
The fundamental theorem of arithmetic states that every integer greater than 1 can be uniquely expressed as a product of prime numbers, up to the order of the factors. This theorem provides the theoretical basis for the prime factorization method.
Euclidean Algorithm and Modular Arithmetic
The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. This principle is related to modular arithmetic, which deals with remainders after division.
Practical Applications of GCF
The greatest common factor has numerous practical applications in various fields.
Simplifying Fractions
One of the most common applications of GCF is simplifying fractions. By dividing both the numerator and the denominator of a fraction by their GCF, the fraction can be reduced to its simplest form.
Example:
Simplify the fraction 8/6.
- The GCF of 8 and 6 is 2.
- Divide both the numerator and the denominator by 2.
- 8 ÷ 2 = 4
- 6 ÷ 2 = 3
- The simplified fraction is 4/3.
Solving Algebraic Problems
GCF is used in algebra to factor expressions and solve equations. Factoring out the GCF simplifies the expression and helps in solving the equation.
Example:
Factor the expression 8x + 6y.
- The GCF of 8 and 6 is 2.
- Factor out the GCF from the expression.
- 8x + 6y = 2(4x + 3y)
Scheduling and Resource Allocation
GCF can be used in scheduling and resource allocation problems to find the largest common interval or quantity that can be used to divide tasks or resources efficiently.
Example:
Suppose you have two tasks, one that takes 8 hours and another that takes 6 hours. To schedule these tasks in the most efficient way, you need to find the largest common interval that can divide both tasks.
- The GCF of 8 and 6 is 2.
- This means you can divide both tasks into 2-hour intervals for scheduling.
Cryptography
In cryptography, GCF is used in various encryption algorithms to ensure the security and integrity of data. The principles of prime numbers and factorization, which are closely related to GCF, are fundamental to modern cryptographic systems.
Common Mistakes to Avoid
When finding the GCF, it is essential to avoid common mistakes that can lead to incorrect results.
Incorrectly Listing Factors
Ensure that all factors are listed for each number. Missing even one factor can lead to an incorrect GCF.
Errors in Prime Factorization
Make sure that the prime factorization is accurate. A mistake in identifying prime factors or their exponents will result in an incorrect GCF.
Misunderstanding the Euclidean Algorithm
Follow the steps of the Euclidean algorithm carefully. Ensure that the remainder is correctly calculated and used in each step.
Confusing GCF with LCM
The greatest common factor (GCF) and the least common multiple (LCM) are different concepts. GCF is the largest number that divides two or more numbers, while LCM is the smallest number that is a multiple of two or more numbers.
Advanced Concepts Related to GCF
Exploring advanced concepts related to GCF can deepen understanding and provide insights into more complex mathematical problems.
GCF of More Than Two Numbers
The concept of GCF can be extended to more than two numbers. The GCF of multiple numbers is the largest number that divides all the numbers without leaving a remainder.
Example:
Find the GCF of 8, 6, and 12.
- Factors of 8: 1, 2, 4, 8
- Factors of 6: 1, 2, 3, 6
- Factors of 12: 1, 2, 3, 4, 6, 12
- Common factors: 1, 2
- GCF: 2
Relatively Prime Numbers
Two numbers are said to be relatively prime or coprime if their GCF is 1. This means that they have no common factors other than 1.
Example:
The numbers 8 and 15 are relatively prime because their GCF is 1.
GCF and LCM Relationship
There is a relationship between the GCF and the least common multiple (LCM) of two numbers. The product of two numbers is equal to the product of their GCF and LCM.
Formula:
a x b = GCF(a, b) x LCM(a, b)
Example:
For the numbers 8 and 6:
- GCF(8, 6) = 2
- LCM(8, 6) = 24
- 8 x 6 = 48
- 2 x 24 = 48
FAQ About Greatest Common Factor
Q: What is the greatest common factor (GCF)? A: The greatest common factor (GCF) is the largest positive integer that divides two or more integers without leaving a remainder.
Q: Why is the GCF important? A: GCF is important for simplifying fractions, solving algebraic problems, understanding divisibility rules, and various real-world applications.
Q: How do you find the GCF of two numbers? A: The GCF can be found using methods like listing factors, prime factorization, and the Euclidean algorithm.
Q: What is the GCF of 8 and 6? A: The GCF of 8 and 6 is 2.
Q: Can the GCF be zero? A: No, the GCF is always a positive integer.
Q: What is the difference between GCF and LCM? A: GCF is the largest number that divides two or more numbers, while LCM is the smallest number that is a multiple of two or more numbers.
Q: How is the GCF used in simplifying fractions? A: By dividing both the numerator and the denominator of a fraction by their GCF, the fraction can be reduced to its simplest form.
Q: What are relatively prime numbers? A: Two numbers are relatively prime if their GCF is 1, meaning they have no common factors other than 1.
Conclusion
Understanding the greatest common factor is essential for various mathematical and practical applications. Whether you're simplifying fractions, solving algebraic equations, or scheduling tasks, the GCF provides a fundamental tool for problem-solving. By mastering the methods to find the GCF and understanding the underlying mathematical principles, you can enhance your mathematical skills and apply them to real-world scenarios effectively. For the specific case of the numbers 8 and 6, the greatest common factor is 2, a result consistently derived through listing factors, prime factorization, and the Euclidean algorithm.
Latest Posts
Latest Posts
-
How To Find The Range Of A Fraction Function
Nov 23, 2025
-
Flow Of Energy And Matter In Ecosystem
Nov 23, 2025
-
What Is The Greatest Common Factor Of 8 And 6
Nov 23, 2025
-
What Is The Mean Of This Sampling Distribution
Nov 23, 2025
-
How Many Centimeters Make A Meter
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 8 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.