Power Series Ln 1 X 1 X
pinupcasinoyukle
Nov 21, 2025 · 11 min read
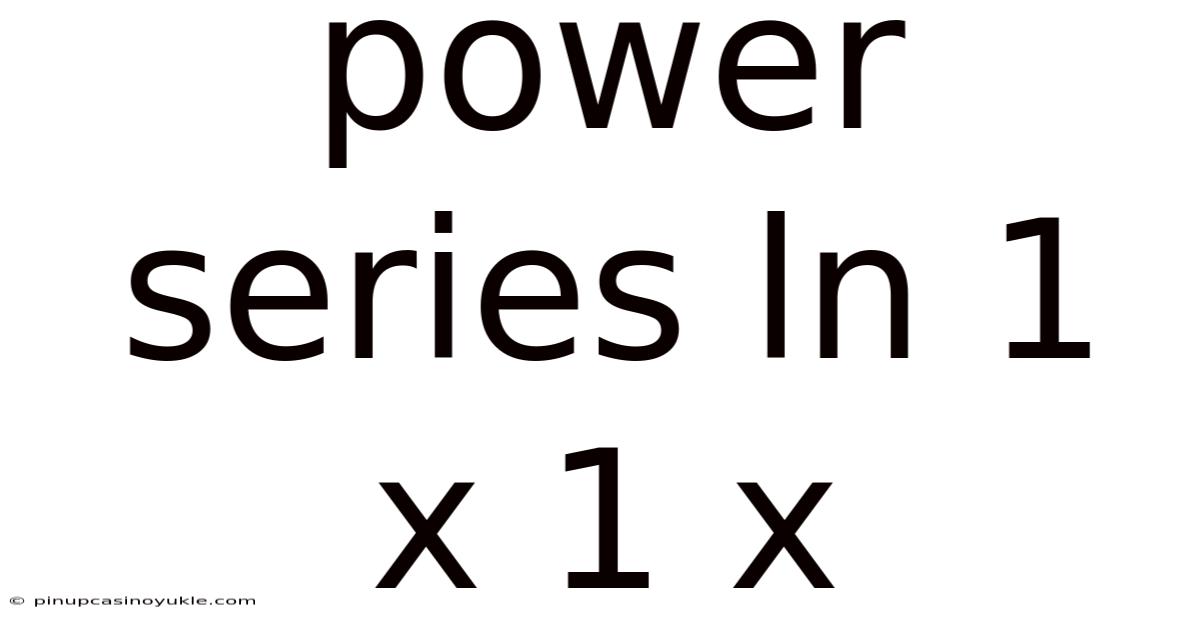
Table of Contents
The power series representation of ln(1+x) unveils a fascinating connection between logarithmic functions and infinite series, offering a powerful tool for approximating values, solving differential equations, and expanding our understanding of mathematical functions. This particular power series, centered at x=0, elegantly expresses the natural logarithm of (1+x) as an infinite sum of terms involving powers of x.
Unveiling the Power Series of ln(1+x)
The power series representation for ln(1+x) is given by:
ln(1 + x) = x - (x²/2) + (x³/3) - (x⁴/4) + (x⁵/5) - ... = ∑ (-1)^(n+1) * (xⁿ/n) for n = 1 to ∞
This series converges for -1 < x ≤ 1. Let's break down this formula and explore its significance.
- The Structure: The series is an alternating sum of terms, where each term is a power of x divided by its corresponding exponent.
- Alternating Sign: The (-1)^(n+1) factor ensures that the terms alternate in sign, a crucial characteristic of this particular power series.
- Convergence: The series converges (approaches a finite value) for values of x within the interval (-1, 1], meaning that the approximation becomes more accurate as more terms are included, provided x is within this range. The convergence is conditional at x=1, meaning that the series converges, but not absolutely.
Deriving the Power Series: A Step-by-Step Approach
The derivation of this power series involves a clever combination of calculus concepts:
1. The Geometric Series Foundation:
We begin with the well-known geometric series:
1/(1 - x) = 1 + x + x² + x³ + x⁴ + ... = ∑ xⁿ for n = 0 to ∞
This series converges for |x| < 1.
2. Substitution for a Strategic Transformation:
Let's substitute '-x' for 'x' in the geometric series:
1/(1 + x) = 1 - x + x² - x³ + x⁴ - ... = ∑ (-1)ⁿ * xⁿ for n = 0 to ∞
This substitution shifts the series to resemble the derivative of ln(1+x).
3. Integration: The Key to Unlocking the Logarithm:
Now, we integrate both sides of the equation with respect to x:
∫ [1/(1 + x)] dx = ∫ [1 - x + x² - x³ + x⁴ - ...] dx
The left side integrates to ln(1 + x) + C, where C is the constant of integration. The right side integrates term by term:
ln(1 + x) + C = x - (x²/2) + (x³/3) - (x⁴/4) + (x⁵/5) - ...
4. Determining the Constant of Integration:
To find the value of C, we can substitute x = 0 into the equation:
ln(1 + 0) + C = 0 - (0²/2) + (0³/3) - (0⁴/4) + ...
ln(1) + C = 0
Since ln(1) = 0, we find that C = 0.
5. The Final Result: The Power Series Unveiled:
Substituting C = 0 back into the equation, we obtain the power series representation for ln(1 + x):
ln(1 + x) = x - (x²/2) + (x³/3) - (x⁴/4) + (x⁵/5) - ... = ∑ (-1)^(n+1) * (xⁿ/n) for n = 1 to ∞
Why is this Power Series Useful? Applications and Significance
The power series representation of ln(1+x) isn't just a mathematical curiosity; it has numerous practical applications:
-
Approximating Logarithm Values: For values of x close to 0, the power series provides a good approximation of ln(1+x). The more terms you include in the series, the more accurate the approximation becomes. This is particularly useful when a calculator isn't readily available.
-
Example: Let's approximate ln(1.1) using the first three terms of the series (x = 0.1):
ln(1.1) ≈ 0.1 - (0.1²/2) + (0.1³/3) = 0.1 - 0.005 + 0.000333... ≈ 0.095333
The actual value of ln(1.1) is approximately 0.095310. Even with just three terms, the approximation is quite accurate.
-
-
Evaluating Difficult Integrals: Sometimes, evaluating an integral involving ln(1+x) directly can be challenging. By substituting the power series representation, the integral can be transformed into an integral of a polynomial, which is often much easier to solve.
-
Example: Consider the integral ∫ ln(1+x) dx. Substituting the power series:
∫ ln(1+x) dx = ∫ [x - (x²/2) + (x³/3) - (x⁴/4) + ...] dx
Integrating term by term:
∫ ln(1+x) dx = (x²/2) - (x³/6) + (x⁴/12) - (x⁵/20) + ... + C
-
-
Solving Differential Equations: Power series methods are frequently used to solve differential equations, especially those that don't have closed-form solutions. If a differential equation involves ln(1+x), its power series representation can be incorporated into the solution process.
-
Theoretical Foundation: The power series representation helps in understanding the properties of the natural logarithm function. It allows us to connect the logarithm to polynomials, providing a bridge between different areas of mathematics.
-
Computer Algorithms: Computers often use power series or similar approximations to calculate logarithmic values, especially when high precision is required. The power series provides a computationally efficient way to evaluate the logarithm function.
Convergence: A Crucial Consideration
As mentioned earlier, the power series for ln(1+x) converges for -1 < x ≤ 1. Understanding the convergence behavior is critical for using the series effectively:
-
Divergence outside the Interval: For values of x outside the interval (-1, 1], the series diverges, meaning that the sum of the terms grows infinitely large and does not approach a finite value. Therefore, the power series representation is not valid for approximating ln(1+x) when x is outside this range.
-
Rate of Convergence: The rate at which the series converges depends on the value of x. The closer x is to 0, the faster the series converges, and the fewer terms are needed to achieve a desired level of accuracy. As x approaches 1 or -1, the convergence becomes slower.
-
Conditional Convergence at x = 1: At x = 1, the series becomes:
1 - (1/2) + (1/3) - (1/4) + (1/5) - ...
This is the alternating harmonic series, which is known to converge to ln(2). However, it converges conditionally, meaning that if the order of the terms is rearranged, the series can converge to a different value or even diverge. This highlights the importance of maintaining the correct order of terms when using the series.
Manipulating the Power Series: Expanding Our Toolkit
The power series for ln(1+x) can be manipulated to derive power series representations for other related functions:
-
Finding the Power Series for ln(1-x):
We can substitute '-x' for 'x' in the power series for ln(1+x):
ln(1 - x) = -x - (x²/2) - (x³/3) - (x⁴/4) - (x⁵/5) - ... = -∑ (xⁿ/n) for n = 1 to ∞
This series converges for -1 ≤ x < 1.
-
Finding the Power Series for ln((1+x)/(1-x)):
Using the properties of logarithms, we know that ln((1+x)/(1-x)) = ln(1+x) - ln(1-x). Therefore, we can subtract the power series for ln(1-x) from the power series for ln(1+x):
ln((1+x)/(1-x)) = [x - (x²/2) + (x³/3) - (x⁴/4) + ...] - [-x - (x²/2) - (x³/3) - (x⁴/4) - ...]
Simplifying, we get:
ln((1+x)/(1-x)) = 2x + (2x³/3) + (2x⁵/5) + (2x⁷/7) + ... = 2∑ (x^(2n-1))/(2n-1) for n = 1 to ∞
This series converges for |x| < 1. This representation is particularly useful because it converges more rapidly than the series for ln(1+x) or ln(1-x), especially for values of x close to 0.
Illustrative Examples: Putting the Power Series to Work
Let's solidify our understanding with a few more examples:
Example 1: Approximating ln(0.9) using the power series for ln(1-x)
We want to approximate ln(0.9), which can be written as ln(1 - 0.1). So, x = 0.1. Using the first three terms of the power series for ln(1-x):
ln(0.9) ≈ -0.1 - (0.1²/2) - (0.1³/3) = -0.1 - 0.005 - 0.000333... ≈ -0.105333
The actual value of ln(0.9) is approximately -0.105361.
Example 2: Finding the power series for x*ln(1+x)
To find the power series for x*ln(1+x), we simply multiply the power series for ln(1+x) by x:
x*ln(1+x) = x * [x - (x²/2) + (x³/3) - (x⁴/4) + ...] = x² - (x³/2) + (x⁴/3) - (x⁵/4) + ... = ∑ (-1)^(n+1) * (x^(n+1)/n) for n = 1 to ∞
Example 3: Using the power series to evaluate a limit
Consider the limit: lim (x->0) [ln(1+x) - x] / x²
Direct substitution leads to an indeterminate form (0/0). However, we can use the power series for ln(1+x):
lim (x->0) [ln(1+x) - x] / x² = lim (x->0) [ (x - (x²/2) + (x³/3) - ...) - x ] / x²
Simplifying:
lim (x->0) [-(x²/2) + (x³/3) - (x⁴/4) + ...] / x² = lim (x->0) [-1/2 + (x/3) - (x²/4) + ...]
As x approaches 0, all the terms with x vanish, leaving:
lim (x->0) [ln(1+x) - x] / x² = -1/2
Common Mistakes to Avoid
When working with the power series for ln(1+x), be mindful of these common pitfalls:
- Ignoring the Convergence Interval: Applying the power series outside the interval of convergence (-1 < x ≤ 1) will lead to incorrect results. Always check that the value of x you're using is within the valid range.
- Truncating the Series Too Early: Using too few terms in the series can result in a poor approximation, especially for values of x that are not close to 0. Consider the desired level of accuracy and include enough terms to achieve it.
- Forgetting the Alternating Sign: The alternating sign is a crucial characteristic of the series. Omitting the (-1)^(n+1) factor will drastically change the result.
- Incorrectly Manipulating the Series: When manipulating the series (e.g., substituting, differentiating, or integrating), ensure that you perform the operations correctly on each term.
- Confusing with Other Logarithm Series: Be careful not to confuse the power series for ln(1+x) with power series for other logarithmic functions or related functions.
The Broader Context: Power Series in Mathematics
The power series representation of ln(1+x) is just one example of the power and versatility of power series in mathematics. Power series are used extensively in:
- Calculus: Representing functions, evaluating limits, finding derivatives and integrals, solving differential equations.
- Complex Analysis: Defining and analyzing complex functions, studying singularities, and developing powerful theorems.
- Numerical Analysis: Approximating function values, solving equations, and developing numerical algorithms.
- Physics and Engineering: Modeling physical phenomena, solving engineering problems, and analyzing systems.
Understanding power series is a fundamental step in mastering many advanced mathematical concepts.
FAQs: Addressing Common Questions
-
Q: What is a power series?
A: A power series is an infinite series of the form ∑ cₙ(x - a)ⁿ, where cₙ are coefficients, x is a variable, and a is the center of the series.
-
Q: Why is the power series centered at x=0 for ln(1+x)?
A: The power series is centered at x=0 because it simplifies the calculations and provides a good approximation of ln(1+x) for values of x close to 0. A Taylor series expansion around another point could also be derived.
-
Q: How many terms should I use for an accurate approximation?
A: The number of terms needed depends on the value of x and the desired level of accuracy. Smaller values of x require fewer terms. You can estimate the error by looking at the magnitude of the next term in the series.
-
Q: Can I use this power series for ln(x) directly?
A: No, the power series is specifically for ln(1+x). To find ln(x), you would need to use a different approach, such as shifting the series or using a Taylor series expansion around a different point. For example, you could write ln(x) = ln(1 + (x-1)) and then expand around x=1.
-
Q: What happens if I try to use the series for x = -2?
A: The series diverges for x = -2, as it's outside the interval of convergence (-1 < x ≤ 1). The approximation will be completely inaccurate and will not converge to a finite value.
Conclusion: Embracing the Power of Infinite Series
The power series representation of ln(1+x) is a testament to the elegance and power of infinite series in mathematics. It provides a valuable tool for approximating logarithmic values, solving integrals and differential equations, and gaining a deeper understanding of the properties of the natural logarithm function. By understanding the derivation, applications, and limitations of this power series, you can unlock a powerful technique for tackling a wide range of mathematical problems. Remember to always consider the convergence interval and the number of terms needed for an accurate approximation. This power series is not just a formula; it's a gateway to a deeper understanding of the interconnectedness of different mathematical concepts.
Latest Posts
Latest Posts
-
Map Of Indian Reservations In Us
Nov 21, 2025
-
What Was The Significance Of The Compromise Of 1877
Nov 21, 2025
-
Why Arent Subscripts Reduced In Covalent Compounds
Nov 21, 2025
-
Power Series Ln 1 X 1 X
Nov 21, 2025
-
Psychology Top Down Vs Bottom Up
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about Power Series Ln 1 X 1 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.