Percentage Of 11 Out Of 15
pinupcasinoyukle
Nov 11, 2025 · 12 min read
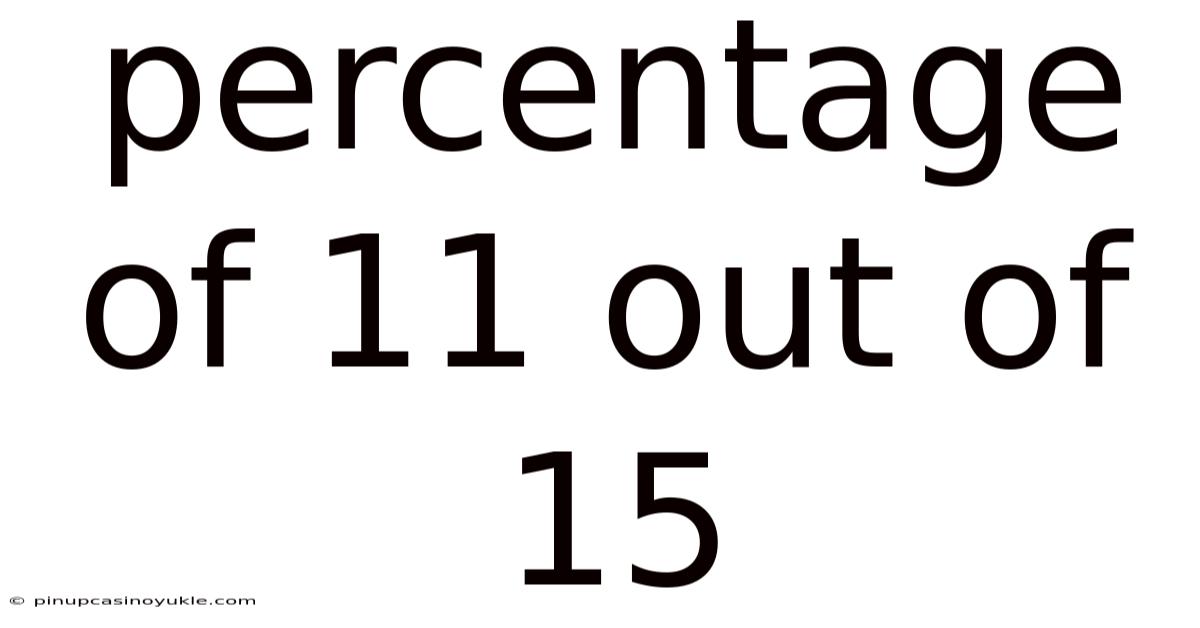
Table of Contents
Calculating percentages is a fundamental skill applicable in various aspects of life, from academic grading to financial analysis. Understanding how to determine what percentage one number represents of another provides valuable insights and facilitates informed decision-making. In this case, determining the percentage of 11 out of 15 requires a straightforward calculation that unveils the proportional relationship between these two numbers.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. It's a ratio that tells us how many parts out of every hundred we have. The word "percent" comes from the Latin "per centum," meaning "out of one hundred." Using percentages makes it easier to compare different proportions and understand relative values.
-
Basic Formula: The fundamental formula for calculating a percentage is:
(Part / Whole) × 100Where:
- Part is the number you want to express as a percentage of the whole.
- Whole is the total or reference number.
-
Why Percentages Matter: Percentages are used everywhere. In finance, they help calculate interest rates, profit margins, and investment returns. In retail, they determine discounts and sales tax. In education, they represent grades and test scores. Understanding percentages allows you to interpret data accurately and make informed decisions.
Calculating the Percentage of 11 Out of 15
Calculating the percentage of 11 out of 15 involves a simple application of the percentage formula. This calculation reveals what proportion 11 represents of the total 15, expressed as a percentage. By following a step-by-step approach, anyone can easily compute this value.
Step-by-Step Calculation
To calculate the percentage of 11 out of 15, follow these steps:
-
Identify the Part and the Whole:
- Part: The number you are interested in, which is 11.
- Whole: The total number, which is 15.
-
Apply the Formula: Use the percentage formula:
(Part / Whole) × 100Substitute the values:
(11 / 15) × 100 -
Divide the Part by the Whole:
11 ÷ 15 = 0.7333 -
Multiply by 100:
0. 7333 × 100 = 73.33 -
Result: Therefore, 11 out of 15 is approximately 73.33%.
Example Scenarios
Understanding how to apply this calculation in real-world scenarios can further solidify your grasp of the concept. Here are a couple of examples:
-
Scenario 1: Quiz Score
Imagine you took a quiz with 15 questions, and you answered 11 correctly. To find out your score as a percentage, you would calculate (11 / 15) × 100, which equals approximately 73.33%. This means you scored 73.33% on the quiz.
-
Scenario 2: Project Completion
Suppose you are working on a project with 15 tasks, and you have completed 11 of them. To determine the percentage of the project you have finished, you calculate (11 / 15) × 100, resulting in approximately 73.33%. This indicates that you have completed 73.33% of the project.
Different Methods to Calculate Percentages
While the basic formula is the most direct way to calculate percentages, there are alternative methods that can be useful in different situations. These methods can provide a deeper understanding of percentages and offer flexibility in problem-solving.
Using Decimals
Converting fractions to decimals before calculating the percentage is a common and straightforward method.
-
Convert to Decimal: Divide the part by the whole to get a decimal.
11 ÷ 15 = 0.7333 -
Multiply by 100: Multiply the decimal by 100 to express it as a percentage.
0. 7333 × 100 = 73.33%
This method is particularly useful when you have a calculator handy, as it simplifies the calculation process.
Using Proportions
Setting up a proportion is another way to find the percentage. A proportion states that two ratios are equal.
-
Set up the Proportion:
11 / 15 = x / 100Here, x represents the percentage we want to find.
-
Cross-Multiply:
15 × x = 11 × 10015x = 1100 -
Solve for x:
x = 1100 / 15x = 73.33
This method is helpful because it reinforces the concept of percentages as ratios and can be applied to various percentage-related problems.
Mental Math Techniques
For quick estimations, mental math techniques can be valuable. These techniques involve approximating the values to simplify the calculation.
- Approximate the Fraction: Recognize that 11/15 is close to 10/15, which simplifies to 2/3.
- Convert to Percentage: Knowing that 2/3 is approximately 66.67%, you can adjust slightly upwards since 11/15 is more than 10/15.
While this method doesn't provide an exact answer, it gives a reasonable estimate, which can be useful in situations where precision is not critical.
Practical Applications of Percentage Calculation
Understanding how to calculate percentages is not just an academic exercise; it has numerous practical applications in everyday life. Whether you're managing your finances, shopping for discounts, or analyzing data, percentages play a crucial role.
Finance
In finance, percentages are essential for calculating interest rates, investment returns, and loan payments.
- Interest Rates: Banks use percentages to express interest rates on savings accounts and loans. Knowing how to calculate these percentages helps you understand the actual cost of borrowing money or the potential earnings from your savings.
- Investment Returns: The performance of investments is often measured in percentages. Calculating the percentage return on an investment allows you to assess its profitability and compare it with other investment options.
- Budgeting: Percentages help in creating and managing a budget. By allocating percentages of your income to different categories (e.g., housing, food, transportation), you can track your spending and ensure you are meeting your financial goals.
Retail
Retailers use percentages to offer discounts, calculate sales tax, and determine profit margins.
- Discounts: Understanding how discounts are calculated helps you determine the actual savings on a product. For example, a 20% discount on an item priced at $50 means you save $10.
- Sales Tax: Sales tax is typically calculated as a percentage of the purchase price. Knowing the sales tax rate allows you to estimate the total cost of your purchase.
- Profit Margins: Retailers calculate profit margins as a percentage of the selling price. This helps them determine the profitability of their products and make pricing decisions.
Education
In education, percentages are used to calculate grades, assess student performance, and compare results.
- Grades: Teachers use percentages to assign grades based on test scores, assignments, and class participation. A percentage score provides a clear indication of a student's performance in a particular subject.
- Standardized Tests: Standardized tests often report scores as percentiles, which indicate the percentage of students who scored below a particular score. This helps in comparing individual performance against a larger group.
- Progress Tracking: Percentages can be used to track student progress over time. By comparing percentage scores on different assessments, educators can identify areas where students are improving or struggling.
Health and Nutrition
Percentages are also used in health and nutrition to understand nutritional information and track health metrics.
- Daily Values: Nutrition labels often list the percentage of daily values for various nutrients. This helps you understand how much of a particular nutrient you are consuming relative to the recommended daily intake.
- Body Fat Percentage: Body fat percentage is a measure of the proportion of body weight that is fat. Tracking body fat percentage can be useful for monitoring fitness progress and overall health.
- Weight Loss: Percentages can be used to track weight loss progress. Calculating the percentage of weight lost helps you visualize your progress and stay motivated.
Data Analysis
In data analysis, percentages are used to summarize and interpret data, identify trends, and make comparisons.
- Market Share: Companies use percentages to measure their market share, which is the proportion of total sales in a market that they control. This helps them assess their competitive position and identify opportunities for growth.
- Survey Results: Survey results are often presented as percentages. This makes it easier to understand the distribution of responses and identify key trends.
- Statistical Analysis: Percentages are used in statistical analysis to calculate proportions, confidence intervals, and significance levels.
Common Mistakes to Avoid
While calculating percentages is generally straightforward, there are common mistakes that people make. Avoiding these mistakes can ensure accuracy and prevent misunderstandings.
Confusing Part and Whole
One of the most common mistakes is confusing the part and the whole in the percentage formula. Always ensure that the part represents the specific quantity you are interested in, and the whole represents the total or reference quantity.
- Example: If you want to find the percentage of apples in a basket containing 10 apples and 5 oranges, the part is 10 (apples), and the whole is 15 (total fruits).
Misinterpreting the Base
Misinterpreting the base when calculating percentage changes can lead to incorrect conclusions. The base is the original value from which the change is calculated.
- Example: If a price increases from $100 to $120, the percentage increase is calculated based on the original price of $100, not the new price of $120. The correct calculation is
(($120 - $100) / $100) × 100 = 20%.
Incorrect Decimal Placement
Incorrect decimal placement can significantly alter the result when converting decimals to percentages. Always ensure that you multiply the decimal by 100 to express it as a percentage.
- Example: If you have a decimal of 0.05, multiplying it by 100 gives you 5%, not 0.05%.
Forgetting to Multiply by 100
Forgetting to multiply by 100 after dividing the part by the whole is a common oversight. This step is essential to express the result as a percentage.
- Example: If you divide 10 by 20, you get 0.5. To express this as a percentage, you must multiply by 100, resulting in 50%.
Rounding Errors
Rounding errors can accumulate and affect the accuracy of the final result, especially when dealing with multiple calculations. To minimize rounding errors, keep intermediate values with several decimal places and round only the final result.
- Example: If you calculate 11/15 as 0.733333, using 0.73 for further calculations can lead to a noticeable difference in the final percentage.
Assuming Percentages are Additive
Assuming that percentages are additive can lead to incorrect conclusions when dealing with percentage changes. Percentage changes are not always additive, especially when they are calculated on different bases.
- Example: If a price increases by 10% and then decreases by 10%, the final price is not the same as the original price. The increase is calculated on the original price, while the decrease is calculated on the increased price.
Advanced Percentage Calculations
Beyond basic percentage calculations, there are more advanced concepts that can be useful in specific situations. Understanding these concepts can enhance your analytical skills and problem-solving abilities.
Percentage Increase and Decrease
Calculating percentage increase and decrease is essential for tracking changes over time and comparing different values.
-
Percentage Increase: The formula for calculating percentage increase is:
((New Value - Original Value) / Original Value) × 100 -
Percentage Decrease: The formula for calculating percentage decrease is:
((Original Value - New Value) / Original Value) × 100
Compound Percentage Change
Compound percentage change involves calculating the cumulative effect of multiple percentage changes over time.
-
Formula: If you have an initial value and a series of percentage changes, the final value can be calculated as:
Final Value = Initial Value × (1 + Change1) × (1 + Change2) × ... × (1 + ChangeN)Where Change1, Change2, ..., ChangeN are the percentage changes expressed as decimals.
Weighted Averages
Weighted averages are used to calculate the average of a set of values, where each value is assigned a different weight.
-
Formula: The formula for calculating a weighted average is:
Weighted Average = (Weight1 × Value1 + Weight2 × Value2 + ... + WeightN × ValueN) / (Weight1 + Weight2 + ... + WeightN)
Percentage Difference
Percentage difference is used to compare two values and express the difference as a percentage of their average.
-
Formula: The formula for calculating percentage difference is:
((Value1 - Value2) / ((Value1 + Value2) / 2)) × 100
Tips and Tricks for Mastering Percentages
Mastering percentages involves not only understanding the formulas but also developing practical skills and intuition. Here are some tips and tricks to help you become more proficient in percentage calculations:
Practice Regularly
Regular practice is essential for mastering any mathematical skill. Work through various percentage-related problems to reinforce your understanding and improve your speed and accuracy.
Use Real-World Examples
Applying percentage calculations to real-world examples can make the learning process more engaging and meaningful. Look for opportunities to use percentages in your daily life, such as calculating discounts while shopping or tracking your spending.
Understand the Context
Always consider the context when working with percentages. Understanding the context can help you avoid common mistakes and interpret the results accurately.
Break Down Complex Problems
Breaking down complex problems into smaller, more manageable steps can make them easier to solve. Identify the key information, apply the appropriate formulas, and work through each step systematically.
Use Technology
Use technology to your advantage. Calculators, spreadsheets, and online tools can help you perform percentage calculations quickly and accurately.
Review Your Work
Always review your work to ensure that you have not made any mistakes. Check your calculations, verify your assumptions, and interpret the results carefully.
The Importance of Estimation
Estimation is a valuable skill that can help you quickly assess the reasonableness of your answers and catch potential errors. Here are some estimation techniques for percentage calculations:
Rounding Numbers
Rounding numbers to the nearest whole number or convenient fraction can simplify the calculation process.
- Example: To estimate 21% of 78, round 21% to 20% and 78 to 80. Then, calculate 20% of 80, which is 16.
Using Benchmark Percentages
Using benchmark percentages, such as 10%, 25%, 50%, and 75%, can provide quick estimates for more complex percentages.
- Example: To estimate 33% of 60, recognize that 33% is approximately 1/3. Then, calculate 1/3 of 60, which is 20.
Visualizing Percentages
Visualizing percentages can help you develop a better understanding of their relative size and magnitude.
- Example: Imagine a pie chart divided into 100 slices. Each slice represents 1%. Visualizing percentages in this way can help you quickly estimate their size relative to the whole.
Calculating the percentage of 11 out of 15 is a fundamental skill with broad applications across various fields. By understanding the basic formula, practicing regularly, and avoiding common mistakes, you can master this skill and use it effectively in your daily life. Whether you're calculating grades, managing finances, or analyzing data, a solid understanding of percentages is essential for success.
Latest Posts
Latest Posts
-
What Are Two Stages Of Photosynthesis
Nov 11, 2025
-
Type Iii Survivorship Curves Are Typical Of Species That Exhibit
Nov 11, 2025
-
What Is The Gcf Of 16 And 40
Nov 11, 2025
-
The Product Of Two Rational Numbers Is
Nov 11, 2025
-
Frida Kahlo Self Portrait With Monkey
Nov 11, 2025
Related Post
Thank you for visiting our website which covers about Percentage Of 11 Out Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.