What Is The Gcf Of 16 And 40
pinupcasinoyukle
Nov 11, 2025 · 9 min read
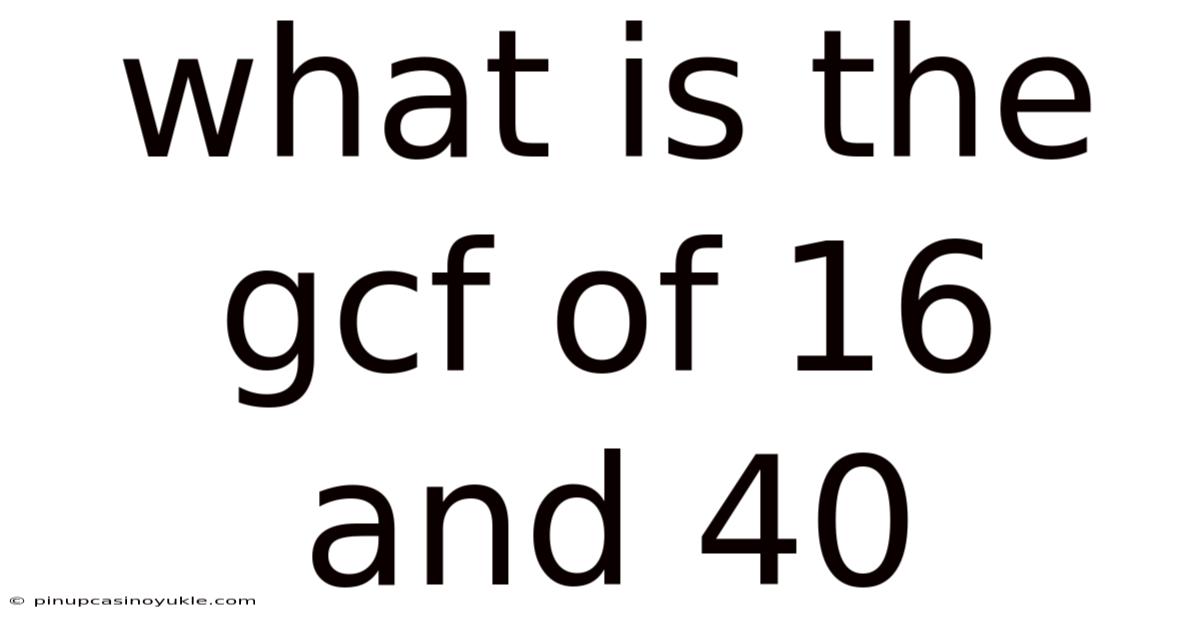
Table of Contents
Let's embark on a journey to unravel the concept of the Greatest Common Factor (GCF), specifically focusing on how to determine the GCF of 16 and 40. The GCF, also known as the Greatest Common Divisor (GCD), is a fundamental concept in mathematics, particularly in number theory. Understanding GCF is crucial for simplifying fractions, solving algebraic equations, and various other mathematical operations.
Understanding the Greatest Common Factor (GCF)
The Greatest Common Factor (GCF) of two or more numbers is the largest positive integer that divides each of the numbers without leaving a remainder. In simpler terms, it's the biggest number that can evenly divide all the given numbers. Finding the GCF is an essential skill in mathematics, enabling us to simplify expressions and solve problems more efficiently.
Why is GCF Important?
- Simplifying Fractions: GCF is used to reduce fractions to their simplest form.
- Solving Equations: It helps in factoring and simplifying algebraic expressions.
- Real-World Applications: GCF is useful in dividing items into equal groups or determining the largest possible size of equal groups.
Methods to Find the GCF
There are several methods to find the GCF of two or more numbers. We will explore the most common methods: listing factors, prime factorization, and the Euclidean algorithm.
1. Listing Factors
This method involves listing all the factors of each number and then identifying the largest factor common to all the numbers.
Steps:
- List the factors of each number:
- Factors of 16: 1, 2, 4, 8, 16
- Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
- Identify common factors:
- Common factors of 16 and 40: 1, 2, 4, 8
- Determine the greatest common factor:
- The greatest common factor of 16 and 40 is 8.
2. Prime Factorization
Prime factorization involves expressing each number as a product of its prime factors. The GCF is then found by multiplying the common prime factors raised to the lowest power they appear in any of the factorizations.
Steps:
- Find the prime factorization of each number:
- Prime factorization of 16: 2 x 2 x 2 x 2 = 2<sup>4</sup>
- Prime factorization of 40: 2 x 2 x 2 x 5 = 2<sup>3</sup> x 5
- Identify common prime factors:
- The common prime factor is 2.
- Determine the lowest power of the common prime factors:
- The lowest power of 2 in the factorizations is 2<sup>3</sup>.
- Multiply the common prime factors raised to the lowest power:
- GCF = 2<sup>3</sup> = 8
3. Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers. It involves repeatedly applying the division algorithm until the remainder is zero. The last non-zero remainder is the GCF.
Steps:
- Divide the larger number by the smaller number and find the remainder:
- 40 ÷ 16 = 2 with a remainder of 8
- If the remainder is zero, the smaller number is the GCF. If not, replace the larger number with the smaller number and the smaller number with the remainder, and repeat the process:
- Now, divide 16 by 8:
- 16 ÷ 8 = 2 with a remainder of 0
- Now, divide 16 by 8:
- The last non-zero remainder is the GCF:
- Since the remainder is now 0, the GCF is 8.
Step-by-Step Guide to Finding the GCF of 16 and 40
To consolidate our understanding, let's walk through each method step-by-step for finding the GCF of 16 and 40.
Method 1: Listing Factors
- List the factors of 16:
- The factors of 16 are the numbers that divide 16 without leaving a remainder.
- Factors of 16: 1, 2, 4, 8, 16
- List the factors of 40:
- The factors of 40 are the numbers that divide 40 without leaving a remainder.
- Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
- Identify the common factors:
- Compare the lists of factors for 16 and 40.
- Common factors: 1, 2, 4, 8
- Determine the greatest common factor:
- From the list of common factors, identify the largest number.
- The greatest common factor of 16 and 40 is 8.
Method 2: Prime Factorization
- Find the prime factorization of 16:
- Break down 16 into its prime factors.
- 16 = 2 x 2 x 2 x 2 = 2<sup>4</sup>
- Find the prime factorization of 40:
- Break down 40 into its prime factors.
- 40 = 2 x 2 x 2 x 5 = 2<sup>3</sup> x 5
- Identify the common prime factors:
- Compare the prime factorizations of 16 and 40.
- The common prime factor is 2.
- Determine the lowest power of the common prime factors:
- The lowest power of 2 in the factorizations is 2<sup>3</sup>.
- Multiply the common prime factors raised to the lowest power:
- GCF = 2<sup>3</sup> = 8
Method 3: Euclidean Algorithm
- Divide the larger number (40) by the smaller number (16) and find the remainder:
- 40 ÷ 16 = 2 with a remainder of 8
- If the remainder is zero, the smaller number is the GCF. If not, replace the larger number with the smaller number and the smaller number with the remainder, and repeat the process:
- Since the remainder is not zero, divide 16 by 8.
- 16 ÷ 8 = 2 with a remainder of 0
- The last non-zero remainder is the GCF:
- The remainder is now 0, so the GCF is the last non-zero remainder, which is 8.
Examples and Practice Problems
To reinforce your understanding, let's look at some examples and practice problems involving GCF.
Example 1: Finding the GCF of 24 and 36
- Listing Factors:
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
- Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
- Common factors: 1, 2, 3, 4, 6, 12
- GCF: 12
- Prime Factorization:
- 24 = 2 x 2 x 2 x 3 = 2<sup>3</sup> x 3
- 36 = 2 x 2 x 3 x 3 = 2<sup>2</sup> x 3<sup>2</sup>
- Common prime factors: 2 and 3
- Lowest powers: 2<sup>2</sup> and 3<sup>1</sup>
- GCF: 2<sup>2</sup> x 3 = 4 x 3 = 12
- Euclidean Algorithm:
- 36 ÷ 24 = 1 with a remainder of 12
- 24 ÷ 12 = 2 with a remainder of 0
- GCF: 12
Example 2: Finding the GCF of 48 and 60
- Listing Factors:
- Factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
- Factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
- Common factors: 1, 2, 3, 4, 6, 12
- GCF: 12
- Prime Factorization:
- 48 = 2 x 2 x 2 x 2 x 3 = 2<sup>4</sup> x 3
- 60 = 2 x 2 x 3 x 5 = 2<sup>2</sup> x 3 x 5
- Common prime factors: 2 and 3
- Lowest powers: 2<sup>2</sup> and 3<sup>1</sup>
- GCF: 2<sup>2</sup> x 3 = 4 x 3 = 12
- Euclidean Algorithm:
- 60 ÷ 48 = 1 with a remainder of 12
- 48 ÷ 12 = 4 with a remainder of 0
- GCF: 12
Practice Problems
- Find the GCF of 18 and 27.
- Find the GCF of 32 and 48.
- Find the GCF of 25 and 75.
- Find the GCF of 14 and 42.
- Find the GCF of 30 and 45.
Tips and Tricks for Finding GCF
- Start with small prime numbers: When using prime factorization, start by dividing by the smallest prime number (2) and work your way up.
- Look for common factors: When listing factors, look for factors that appear in all the lists to save time.
- Use the Euclidean algorithm for large numbers: The Euclidean algorithm is particularly useful when dealing with large numbers, as it is more efficient than listing factors or prime factorization.
- Practice regularly: The more you practice, the better you will become at finding the GCF.
Real-World Applications of GCF
Understanding GCF is not just an academic exercise; it has several practical applications in real life.
- Dividing Items into Equal Groups: Suppose you have 16 apples and 40 oranges and want to divide them into equal groups. To find the largest number of groups you can make, you need to find the GCF of 16 and 40, which is 8. This means you can make 8 groups, each containing 2 apples and 5 oranges.
- Simplifying Fractions: GCF is used to simplify fractions to their simplest form. For example, to simplify the fraction 16/40, you divide both the numerator and the denominator by their GCF, which is 8. This gives you the simplified fraction 2/5.
- Construction and Design: In construction, GCF can be used to determine the largest possible size of tiles that can be used to cover a floor without cutting any tiles.
- Scheduling: GCF can be used to schedule events or tasks that occur at regular intervals. For example, if one task occurs every 16 days and another occurs every 40 days, the GCF can help determine when both tasks will occur on the same day.
Common Mistakes to Avoid
- Confusing GCF with LCM: The Greatest Common Factor (GCF) is often confused with the Least Common Multiple (LCM). Remember that GCF is the largest number that divides into the given numbers, while LCM is the smallest number that the given numbers divide into.
- Incorrect Prime Factorization: Ensure that you correctly identify the prime factors of each number. Double-check your work to avoid mistakes.
- Missing Common Factors: When listing factors, make sure you don't miss any common factors. It's helpful to be systematic in your approach.
- Stopping Too Early in the Euclidean Algorithm: Continue the Euclidean algorithm until the remainder is zero. The last non-zero remainder is the GCF.
Advanced Topics Related to GCF
- GCF of More Than Two Numbers: The concept of GCF can be extended to more than two numbers. To find the GCF of multiple numbers, you can find the GCF of the first two numbers, then find the GCF of that result and the next number, and so on.
- Relationship Between GCF and LCM: There is a relationship between the GCF and LCM of two numbers. The product of two numbers is equal to the product of their GCF and LCM. That is, A x B = GCF(A, B) x LCM(A, B).
- Applications in Cryptography: GCF and related concepts are used in cryptography for key generation and encryption algorithms.
Conclusion
Finding the Greatest Common Factor (GCF) of two numbers, such as 16 and 40, is a fundamental skill in mathematics with various practical applications. Whether you choose to list factors, use prime factorization, or apply the Euclidean algorithm, understanding the process and practicing regularly will enhance your proficiency. In the case of 16 and 40, the GCF is 8, meaning that 8 is the largest number that divides both 16 and 40 without leaving a remainder. By mastering GCF, you gain a valuable tool for simplifying fractions, solving equations, and tackling real-world problems.
Latest Posts
Latest Posts
-
Substances Enter Any Plant Or Animal By Passing Through
Nov 11, 2025
-
Does Electronegativity Increase Down A Group
Nov 11, 2025
-
How To Find The Mean Of A Binomial Distribution
Nov 11, 2025
-
How Did The Great Compromise Affect The Government
Nov 11, 2025
-
Find X As A Function Of Y
Nov 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 16 And 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.