Is 3 5 Greater Than 4 8
pinupcasinoyukle
Nov 05, 2025 · 9 min read
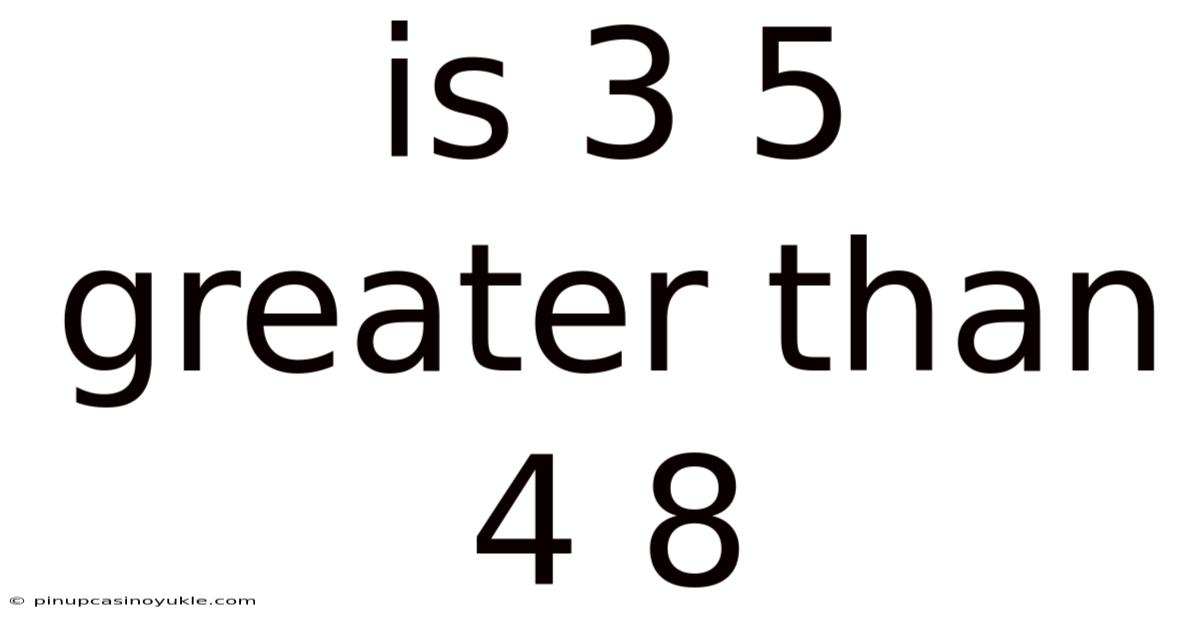
Table of Contents
Is 3/5 Greater Than 4/8? A Comprehensive Guide
Understanding how to compare fractions is a fundamental skill in mathematics. At first glance, determining whether 3/5 is greater than 4/8 might seem straightforward. However, it requires a systematic approach to ensure accuracy. This article will explore various methods to compare these fractions, providing you with a clear understanding and practical tools to tackle similar problems.
Introduction to Comparing Fractions
Fractions represent parts of a whole. Comparing them involves determining which fraction represents a larger portion of that whole. Several methods can be used, including finding a common denominator, converting to decimals, and cross-multiplication. Each method offers a unique perspective and can be applied based on the specific fractions being compared.
Before diving into the comparison of 3/5 and 4/8, let's define some key terms:
- Numerator: The top number in a fraction, indicating how many parts of the whole are being considered.
- Denominator: The bottom number in a fraction, indicating the total number of equal parts that make up the whole.
- Equivalent Fractions: Fractions that represent the same value, even though they have different numerators and denominators (e.g., 1/2 and 2/4).
Understanding these terms is crucial for effectively comparing fractions. Now, let's explore different methods to determine if 3/5 is greater than 4/8.
Method 1: Finding a Common Denominator
One of the most reliable methods for comparing fractions is to find a common denominator. This involves converting both fractions to have the same denominator, making it easier to compare their numerators directly.
Steps to find a common denominator:
- Identify the denominators: In our case, the denominators are 5 and 8.
- Find the least common multiple (LCM): The LCM of 5 and 8 is the smallest number that both 5 and 8 divide into evenly. Multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40, ... and multiples of 8 are 8, 16, 24, 32, 40, .... The LCM of 5 and 8 is 40.
- Convert each fraction to an equivalent fraction with the common denominator:
- To convert 3/5 to a fraction with a denominator of 40, multiply both the numerator and the denominator by 8: (3 * 8) / (5 * 8) = 24/40
- To convert 4/8 to a fraction with a denominator of 40, multiply both the numerator and the denominator by 5: (4 * 5) / (8 * 5) = 20/40
- Compare the numerators: Now that both fractions have the same denominator, we can compare their numerators. We have 24/40 and 20/40. Since 24 is greater than 20, 24/40 is greater than 20/40.
Therefore, 3/5 is greater than 4/8 because 24/40 is greater than 20/40.
Method 2: Converting to Decimals
Another straightforward method to compare fractions is to convert them to decimals. This allows you to compare the fractions using familiar decimal notation.
Steps to convert fractions to decimals:
- Divide the numerator by the denominator:
- For 3/5, divide 3 by 5: 3 ÷ 5 = 0.6
- For 4/8, divide 4 by 8: 4 ÷ 8 = 0.5
- Compare the decimal values: Comparing 0.6 and 0.5, it's clear that 0.6 is greater than 0.5.
Therefore, 3/5 is greater than 4/8 because 0.6 is greater than 0.5.
Method 3: Cross-Multiplication
Cross-multiplication is a quick and efficient method to compare two fractions. This method involves multiplying the numerator of one fraction by the denominator of the other and comparing the results.
Steps for cross-multiplication:
- Cross-multiply the fractions:
- Multiply the numerator of the first fraction (3) by the denominator of the second fraction (8): 3 * 8 = 24
- Multiply the numerator of the second fraction (4) by the denominator of the first fraction (5): 4 * 5 = 20
- Compare the results: Compare the two products obtained from the cross-multiplication. If the first product is greater than the second product, then the first fraction is greater than the second fraction. In this case, 24 is greater than 20.
Therefore, 3/5 is greater than 4/8 because 24 is greater than 20.
Method 4: Simplification
Sometimes, fractions can be simplified before comparison, making the process easier. In this case, 4/8 can be simplified.
Steps for simplification:
- Simplify the fraction:
- The fraction 4/8 can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD of 4 and 8 is 4.
- Divide both the numerator and the denominator by 4: (4 ÷ 4) / (8 ÷ 4) = 1/2
- Compare the simplified fraction: Now, we compare 3/5 with 1/2. We can use any of the previous methods to compare these fractions. Let's use the common denominator method.
- The LCM of 5 and 2 is 10.
- Convert 3/5 to a fraction with a denominator of 10: (3 * 2) / (5 * 2) = 6/10
- Convert 1/2 to a fraction with a denominator of 10: (1 * 5) / (2 * 5) = 5/10
- Compare the numerators: 6/10 is greater than 5/10.
Therefore, 3/5 is greater than 4/8 because 3/5 is greater than 1/2.
Visual Representation: Using Diagrams
Visual aids can be incredibly helpful in understanding and comparing fractions. Representing fractions using diagrams allows for a more intuitive understanding of their relative sizes.
Diagram for 3/5:
Imagine a rectangle divided into 5 equal parts. Shade 3 of these parts. The shaded area represents 3/5 of the whole rectangle.
Diagram for 4/8:
Imagine another identical rectangle divided into 8 equal parts. Shade 4 of these parts. The shaded area represents 4/8 of the whole rectangle.
By visually comparing the two rectangles, you can see that the shaded area in the 3/5 diagram is larger than the shaded area in the 4/8 diagram. This provides a visual confirmation that 3/5 is greater than 4/8.
Furthermore, you can also visualize 4/8 as being equivalent to 1/2. If you divide the second rectangle into only two equal parts, each part would represent 1/2. The 4 shaded parts out of 8 are equivalent to 1 shaded part out of 2.
Real-World Applications
Understanding how to compare fractions is not just a theoretical exercise; it has practical applications in various real-world scenarios. Here are a few examples:
- Cooking: When following a recipe, you might need to adjust ingredient quantities. For example, if a recipe calls for 3/5 cup of flour and you only have a 1/2 cup measuring tool, you need to know if 1/2 cup is enough or if you need to use more.
- Construction: In construction, measurements often involve fractions. Comparing fractions is essential for ensuring accurate cuts and fits. For example, a carpenter might need to determine if a 3/5 inch thick piece of wood is thicker than a 4/8 inch thick piece.
- Finance: Comparing fractions can be useful in understanding financial ratios and proportions. For example, if one investment represents 3/5 of your portfolio and another represents 4/8, you can easily determine which investment is the larger portion.
- Time Management: When planning your day, you might allocate fractions of your time to different activities. Comparing these fractions helps you prioritize and manage your time effectively. For example, if you spend 3/5 of your day working and 4/8 of your day sleeping, you can easily see that you spend more time working than sleeping.
- Sports: In sports, statistics often involve fractions. Comparing fractions can help you analyze player performance and make informed decisions. For example, if one basketball player makes 3/5 of their free throws and another makes 4/8, you can determine which player has a better free throw percentage.
Common Mistakes to Avoid
When comparing fractions, there are several common mistakes that students often make. Being aware of these mistakes can help you avoid them and ensure accurate comparisons.
- Incorrectly Applying Cross-Multiplication: One common mistake is to incorrectly apply cross-multiplication. Make sure to multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa.
- Failing to Find the Least Common Multiple (LCM): When using the common denominator method, failing to find the LCM can lead to unnecessarily large denominators, making the comparison more difficult.
- Ignoring Simplification: Sometimes, simplifying fractions can make the comparison process much easier. Ignoring this step can lead to more complex calculations and a higher chance of error.
- Comparing Numerators or Denominators Directly Without a Common Denominator: A frequent mistake is to directly compare the numerators or denominators without first ensuring that the fractions have a common denominator. This can lead to incorrect conclusions.
- Misunderstanding Decimal Conversions: When converting fractions to decimals, make sure to perform the division correctly. A small error in the division can lead to an incorrect decimal value and an inaccurate comparison.
Advanced Techniques
While the methods described above are sufficient for most fraction comparison problems, there are some advanced techniques that can be useful in more complex scenarios.
- Benchmarking: This involves comparing both fractions to a common benchmark fraction, such as 1/2. For example, if one fraction is clearly greater than 1/2 and the other is less than 1/2, the comparison becomes straightforward.
- Using Percentages: Converting fractions to percentages can provide another way to compare them. For example, 3/5 is equal to 60%, and 4/8 is equal to 50%. Comparing 60% and 50% is straightforward.
- Approximation: In some cases, you can approximate the fractions to make a quick comparison. For example, if you have a fraction like 7/15, you can approximate it to 1/2 for a rough comparison.
Conclusion
In conclusion, 3/5 is greater than 4/8. This can be demonstrated using several methods, including finding a common denominator, converting to decimals, cross-multiplication, and simplification. Each method provides a unique approach to comparing fractions and reinforces the understanding of fractional values. By mastering these techniques, you can confidently compare fractions in various mathematical and real-world scenarios. Remember to practice regularly and be mindful of common mistakes to ensure accuracy. With a solid understanding of fraction comparison, you'll be well-equipped to tackle more advanced mathematical concepts.
Latest Posts
Latest Posts
-
The Energy Of A Moving Object Is Called
Nov 05, 2025
-
Interpreting Graphs Of Proportional Relationships Worksheets
Nov 05, 2025
-
What Is 30 Percent Of 20
Nov 05, 2025
-
Anything Raised To A Power Of Zero Is Always
Nov 05, 2025
-
Find The Least Common Denominator Calculator
Nov 05, 2025
Related Post
Thank you for visiting our website which covers about Is 3 5 Greater Than 4 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.