What Is 30 Percent Of 20
pinupcasinoyukle
Nov 05, 2025 · 8 min read
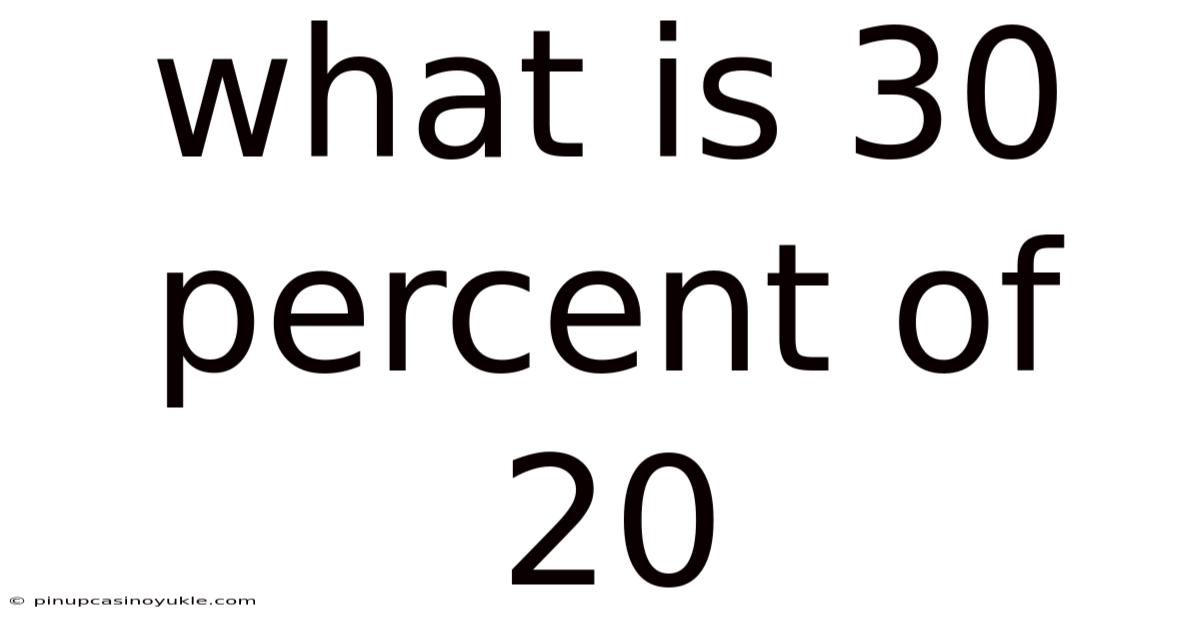
Table of Contents
Calculating percentages is a fundamental skill applicable in various everyday scenarios, from figuring out discounts at the store to understanding financial reports. Understanding what "30 percent of 20" is, involves a simple yet crucial concept that forms the basis for more complex calculations. This article will guide you through the process, offering a clear explanation and practical examples to solidify your comprehension.
Understanding Percentages
Percentage simply means "per hundred" or "out of 100". Therefore, when we say 30 percent, we mean 30 out of 100. To find a percentage of a number, we convert the percentage into a decimal or fraction and then multiply it by the number.
Converting Percentage to Decimal
To convert a percentage to a decimal, you divide the percentage by 100. For example:
30% = 30 / 100 = 0.3
This decimal form is what we'll use in our calculation.
Converting Percentage to Fraction
Alternatively, you can convert a percentage to a fraction by placing it over 100 and simplifying if possible. For example:
30% = 30 / 100 = 3 / 10
This fractional form can also be used in the calculation.
Calculating 30 Percent of 20
Now that we understand how to convert percentages to decimals or fractions, let’s calculate 30 percent of 20 using both methods.
Method 1: Using Decimal Form
-
Convert the percentage to a decimal:
30% = 0.3
-
Multiply the decimal by the number:
- 3 * 20 = 6
Therefore, 30 percent of 20 is 6.
Method 2: Using Fractional Form
-
Convert the percentage to a fraction:
30% = 3 / 10
-
Multiply the fraction by the number:
(3 / 10) * 20 = (3 * 20) / 10 = 60 / 10 = 6
Again, we find that 30 percent of 20 is 6.
Practical Examples
To further illustrate the concept, let’s consider a few practical examples where calculating percentages might be useful.
Example 1: Discount Calculation
Suppose you want to buy a shirt that costs $20, and it is on sale for 30% off. How much money will you save?
-
Identify the percentage and the original price:
Discount = 30%
Original Price = $20
-
Calculate the discount amount:
Discount Amount = 30% of $20 = 0.3 * $20 = $6
You will save $6 on the shirt.
Example 2: Test Scores
Imagine you took a test with 20 questions, and you got 30% of the questions wrong. How many questions did you answer incorrectly?
-
Identify the percentage and the total number of questions:
Percentage Wrong = 30%
Total Questions = 20
-
Calculate the number of incorrect questions:
Incorrect Questions = 30% of 20 = 0.3 * 20 = 6
You answered 6 questions incorrectly.
Example 3: Budget Allocation
Let’s say you have a budget of $20, and you want to allocate 30% of it for entertainment. How much money can you spend on entertainment?
-
Identify the percentage and the total budget:
Percentage for Entertainment = 30%
Total Budget = $20
-
Calculate the amount for entertainment:
Entertainment Budget = 30% of $20 = 0.3 * $20 = $6
You can spend $6 on entertainment.
Alternative Methods for Calculation
Besides the decimal and fractional methods, there are other ways to calculate percentages that can be helpful in different situations.
Using a Calculator
Most calculators have a percentage button (%) that simplifies the calculation process. To find 30 percent of 20:
- Enter 20 into the calculator.
- Press the multiplication button (*).
- Enter 30.
- Press the percentage button (%).
- The calculator will display 6.
Mental Math Techniques
Mental math can be a quick and efficient way to calculate percentages, especially for simple numbers. Here are a few techniques:
-
Finding 10%:
To find 10% of a number, simply divide the number by 10. For example, 10% of 20 is 20 / 10 = 2.
-
Finding 30%:
Since 30% is three times 10%, you can find 10% and then multiply it by 3. For example, if 10% of 20 is 2, then 30% of 20 is 2 * 3 = 6.
-
Breaking Down Percentages:
You can break down percentages into smaller, more manageable parts. For example, to find 30% of 20, you can think of it as (10% of 20) + (10% of 20) + (10% of 20) = 2 + 2 + 2 = 6.
Common Mistakes to Avoid
When calculating percentages, it’s easy to make mistakes if you’re not careful. Here are some common errors to avoid:
-
Forgetting to Convert to Decimal or Fraction:
One of the most common mistakes is forgetting to convert the percentage to a decimal or fraction before multiplying. For example, incorrectly calculating 30% of 20 as 30 * 20 = 600, instead of 0.3 * 20 = 6.
-
Misunderstanding the Base Number:
Ensure you are clear about what number you are taking the percentage of. For example, confusing 30% of 20 with 20% of 30 can lead to errors (although in this specific case, both yield the same result).
-
Incorrectly Simplifying Fractions:
When using the fractional method, double-check that you have simplified the fraction correctly. For example, simplifying 30/100 to 3/10 is correct, but an incorrect simplification could lead to a wrong answer.
-
Rounding Errors:
In some cases, percentages may result in decimals that need to be rounded. Be mindful of when and how you round to maintain accuracy.
Advanced Applications of Percentages
Understanding how to calculate percentages is not only useful for simple calculations but also forms the basis for more advanced applications in various fields.
Finance
In finance, percentages are used extensively to calculate interest rates, investment returns, and profit margins. For example:
-
Interest Rates:
When you deposit money in a savings account, the bank pays you interest, often expressed as a percentage. If you deposit $100 in an account with a 5% annual interest rate, you will earn $5 in interest after one year.
-
Investment Returns:
Investors use percentages to measure the performance of their investments. If you invest $1,000 in a stock and it increases in value by $100, your return on investment is 10%.
-
Profit Margins:
Businesses use percentages to calculate their profit margins. If a company sells a product for $20 and it costs $14 to produce, the profit is $6. The profit margin is (6 / 20) * 100 = 30%.
Statistics
Percentages are also commonly used in statistics to represent data and analyze trends. For example:
-
Survey Results:
When conducting a survey, the results are often expressed as percentages. If 60 out of 200 people surveyed prefer a certain product, that represents 30% of the sample.
-
Demographics:
Demographic data, such as population distribution, is often presented in percentages. For example, if 30% of a city’s population is under the age of 25, this gives a clear indication of the age demographics.
Retail
In retail, percentages are crucial for pricing strategies, discounts, and sales analysis. For example:
-
Discounts:
Retailers use discounts to attract customers. A 30% discount on an item that originally costs $20 reduces the price by $6, making the new price $14.
-
Sales Growth:
Retailers track sales growth as a percentage to measure their performance. If a store’s sales increase from $10,000 to $13,000 in a year, the sales growth is (3000 / 10000) * 100 = 30%.
Real-World Applications
Let's look at more real-world scenarios where calculating percentages is essential.
Calculating Tips
When dining at a restaurant, it’s customary to leave a tip for the server. If your bill is $20 and you want to leave a 20% tip:
-
Identify the bill amount and the tip percentage:
Bill Amount = $20
Tip Percentage = 20%
-
Calculate the tip amount:
Tip Amount = 20% of $20 = 0.20 * $20 = $4
You would leave a $4 tip.
Understanding Taxes
Taxes are often calculated as a percentage of income or purchase price. If you buy an item for $20 and the sales tax is 6%:
-
Identify the item price and the tax percentage:
Item Price = $20
Tax Percentage = 6%
-
Calculate the tax amount:
Tax Amount = 6% of $20 = 0.06 * $20 = $1.20
The sales tax on the item is $1.20.
Measuring Progress
Percentages can be used to measure progress towards a goal. If you need to read a 20-page document and you have read 30% of it:
-
Identify the total pages and the percentage read:
Total Pages = 20
Percentage Read = 30%
-
Calculate the number of pages read:
Pages Read = 30% of 20 = 0.3 * 20 = 6
You have read 6 pages.
Tips for Improving Accuracy
To ensure accuracy when calculating percentages, consider the following tips:
-
Double-Check Your Calculations:
Always double-check your calculations, especially when dealing with important financial or statistical data.
-
Use Calculators or Software:
For complex calculations, use calculators or software tools to minimize the risk of human error.
-
Understand the Context:
Make sure you understand the context of the problem and what the percentage represents. This will help you avoid misinterpretations and errors.
-
Practice Regularly:
The more you practice calculating percentages, the more confident and accurate you will become.
Conclusion
Calculating "30 percent of 20" is a simple yet fundamental concept that has wide-ranging applications in everyday life. Whether you're figuring out discounts, calculating tips, or understanding financial reports, mastering percentages is an invaluable skill. By understanding the basic principles, practicing regularly, and avoiding common mistakes, you can confidently apply this knowledge in various situations. Remember, a percentage is simply a fraction out of 100, and with the right approach, you can easily calculate it for any number.
Latest Posts
Latest Posts
-
Using Composition Of Functions To Determine Inverse
Nov 05, 2025
-
Which Equation Could Be Solved Using The Graph Above
Nov 05, 2025
-
How To Do Proofs In Geometry
Nov 05, 2025
-
Equivalent Fractions On A Number Line
Nov 05, 2025
-
Difference Between The Endocrine System And The Nervous System
Nov 05, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.