Is 1 2 Greater Than 3 8
pinupcasinoyukle
Nov 21, 2025 · 8 min read
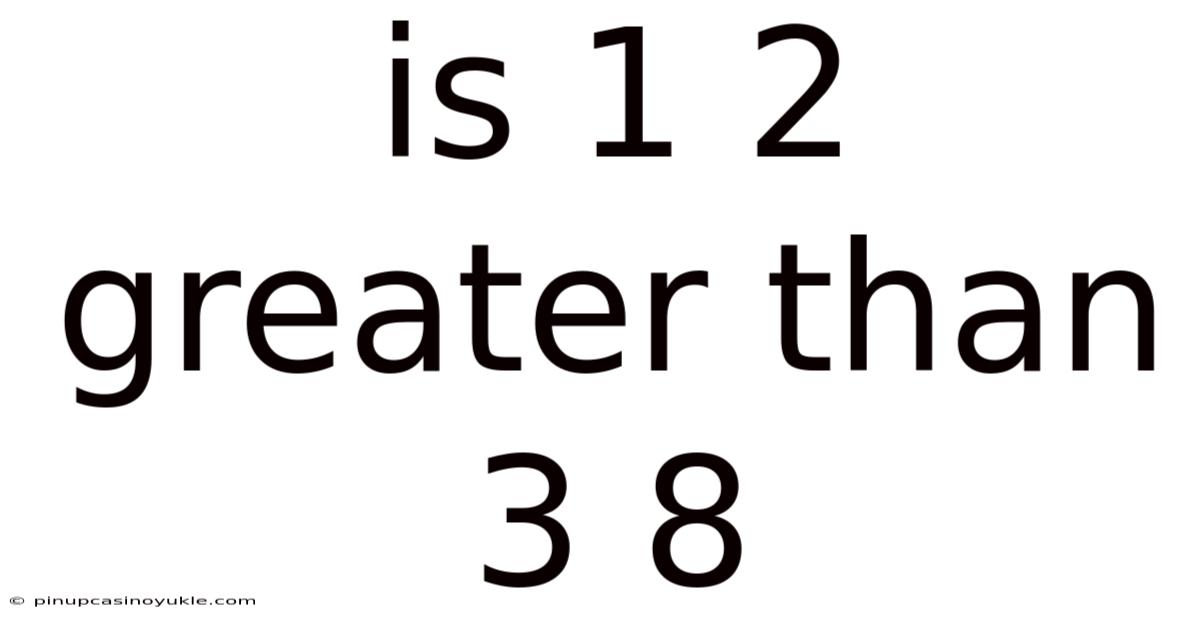
Table of Contents
Navigating the realm of fractions might seem daunting at first, but with a clear understanding of basic principles, comparing seemingly complex fractions like 1/2 and 3/8 becomes surprisingly straightforward. This article will guide you through the process of determining whether 1/2 is indeed greater than 3/8, exploring various methods, providing visual aids, and touching upon the underlying mathematical concepts. By the end, you'll not only know the answer but also possess the skills to confidently compare any fractions you encounter.
Understanding Fractions: The Foundation
Before diving into the comparison, let's solidify our understanding of what fractions represent. A fraction, in its simplest form, expresses a part of a whole. It's written as a/b, where 'a' is the numerator (the top number) representing the number of parts we have, and 'b' is the denominator (the bottom number) indicating the total number of equal parts the whole is divided into.
- Numerator: Indicates the number of parts we have.
- Denominator: Indicates the total number of equal parts the whole is divided into.
Think of a pizza cut into slices. If the pizza is cut into 8 equal slices (denominator = 8), and you take 3 slices (numerator = 3), you have 3/8 of the pizza. Similarly, if the same pizza is cut into 2 equal slices (denominator = 2), and you take 1 slice (numerator = 1), you have 1/2 of the pizza.
Method 1: Finding a Common Denominator
The most reliable and widely used method for comparing fractions is to find a common denominator. This involves converting the fractions so they both have the same denominator, allowing for a direct comparison of their numerators.
Here's how it works for 1/2 and 3/8:
- Identify the denominators: In our case, the denominators are 2 and 8.
- Find the Least Common Multiple (LCM): The LCM of 2 and 8 is 8. This means 8 is the smallest number that both 2 and 8 divide into evenly.
- Convert the fractions:
- To convert 1/2 to a fraction with a denominator of 8, we need to multiply both the numerator and denominator by the same number. In this case, we multiply by 4 (because 2 * 4 = 8).
- (1 * 4) / (2 * 4) = 4/8
- The fraction 3/8 already has the desired denominator, so no conversion is needed.
- To convert 1/2 to a fraction with a denominator of 8, we need to multiply both the numerator and denominator by the same number. In this case, we multiply by 4 (because 2 * 4 = 8).
- Compare the numerators: Now we have 4/8 and 3/8. Since 4 is greater than 3, we can conclude that 4/8 is greater than 3/8.
Therefore, 1/2 (which is equivalent to 4/8) is greater than 3/8.
Method 2: Cross-Multiplication
Cross-multiplication offers a quick and efficient way to compare two fractions. This method avoids the explicit need to find a common denominator.
Here's how to apply it to 1/2 and 3/8:
- Write the fractions side-by-side: 1/2 and 3/8
- Cross-multiply: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa.
- 1 * 8 = 8
- 2 * 3 = 6
- Compare the results: The larger product corresponds to the larger fraction. Since 8 is greater than 6, 1/2 is greater than 3/8.
This method essentially performs the same operation as finding a common denominator but in a more condensed form.
Method 3: Converting to Decimals
Another way to compare fractions is by converting them to decimals. This allows for a direct comparison using our understanding of decimal values.
Let's convert 1/2 and 3/8 to decimals:
- Divide the numerator by the denominator:
- 1/2 = 0.5
- 3/8 = 0.375
- Compare the decimals: 0.5 is greater than 0.375.
Therefore, 1/2 is greater than 3/8. This method is particularly useful when dealing with fractions that are not easily converted to a common denominator.
Method 4: Visual Representation
Visualizing fractions can provide a concrete understanding and make comparisons more intuitive. Here are a couple of visual methods:
-
Using Fraction Bars: Imagine two identical bars. Divide the first bar into two equal parts and shade one part to represent 1/2. Divide the second bar into eight equal parts and shade three parts to represent 3/8. By comparing the shaded areas, you can visually see that the shaded area representing 1/2 is larger than the shaded area representing 3/8.
-
Using a Number Line: Draw a number line from 0 to 1. Mark the position of 1/2 (which is halfway between 0 and 1) and the position of 3/8. To find the position of 3/8, divide the line between 0 and 1 into eight equal parts and mark the third division. You'll observe that 1/2 is located to the right of 3/8, indicating that 1/2 is greater.
Why Finding a Common Denominator Works: A Deeper Dive
The effectiveness of finding a common denominator lies in the fundamental principle of comparing like quantities. When fractions have the same denominator, they are essentially divided into the same number of equal parts. This allows us to directly compare the number of parts represented by the numerator.
Think of it like comparing apples and oranges. You can't directly say which group is larger without knowing the size of each fruit. But if you convert everything to, say, cubic inches of fruit volume, then you can directly compare the volumes. Finding a common denominator is analogous to converting fractions to a common "unit" (the size of each fractional part).
Real-World Applications
Understanding how to compare fractions is not just a mathematical exercise; it has practical applications in everyday life. Here are a few examples:
-
Cooking: Recipes often use fractions to specify ingredient quantities. Knowing how to compare fractions allows you to adjust recipes accurately. For example, if a recipe calls for 1/4 cup of sugar and you only have a measuring cup that measures in eighths, you can determine that 1/4 is equivalent to 2/8.
-
Measuring: When measuring lengths or distances, you might encounter fractions of an inch or a foot. Comparing these fractions helps you determine the precise measurements.
-
Financial Planning: Understanding fractions is crucial for budgeting and managing finances. For instance, if you're trying to determine which loan has a lower interest rate (expressed as a fraction), you need to be able to compare those fractions.
-
Time Management: Fractions often come into play when planning your day. If you allocate 1/3 of your day to work and 1/6 to exercise, comparing these fractions can help you understand how much time you're dedicating to each activity.
Common Mistakes to Avoid
While comparing fractions can be straightforward, it's important to avoid common pitfalls:
-
Incorrectly Finding the LCM: Ensure you correctly identify the least common multiple of the denominators. A common mistake is choosing a common multiple that is not the least common multiple, leading to unnecessary complications in the comparison.
-
Forgetting to Multiply Both Numerator and Denominator: When converting to a common denominator, remember to multiply both the numerator and denominator by the same factor. Multiplying only one will change the value of the fraction.
-
Directly Comparing Numerators Without a Common Denominator: This is a fundamental error. You cannot directly compare the numerators unless the fractions have the same denominator.
-
Misinterpreting Decimal Values: Ensure you correctly interpret the decimal values after converting the fractions. Pay attention to the place values to avoid errors in comparison.
Advanced Fraction Comparisons
While the methods described above are sufficient for most basic comparisons, there are scenarios where more advanced techniques might be helpful:
-
Comparing Multiple Fractions: When comparing more than two fractions, it's often easiest to find a common denominator for all of them. This allows for a direct comparison of all the numerators.
-
Comparing Fractions with Large Denominators: When dealing with fractions with very large denominators, finding the LCM can be cumbersome. In such cases, converting to decimals might be a more efficient approach.
-
Using Benchmarks: Benchmarks like 1/2, 1/4, and 3/4 can be helpful for quickly estimating the relative size of fractions. For example, if you're comparing a fraction to 1/2, you can quickly determine if it's greater or less than 1/2 without performing complex calculations.
The Importance of Practice
Like any mathematical skill, proficiency in comparing fractions requires practice. The more you practice, the more comfortable you'll become with the different methods and the faster you'll be able to perform comparisons.
Here are some ways to practice:
- Work through practice problems: Numerous online resources and textbooks offer practice problems on comparing fractions.
- Create your own problems: Make up your own fractions and compare them using different methods.
- Incorporate fractions into everyday activities: Look for opportunities to use fractions in real-world scenarios, such as cooking, measuring, or budgeting.
Conclusion: 1/2 vs. 3/8 – The Verdict
Through various methods, including finding a common denominator, cross-multiplication, converting to decimals, and visual representations, we have conclusively demonstrated that 1/2 is indeed greater than 3/8. This understanding of fraction comparison extends beyond this specific example, providing a valuable tool for problem-solving in mathematics and real-world scenarios. Embrace the different methods, practice regularly, and you'll master the art of fraction comparison with confidence. Remember, fractions are not just abstract numbers; they represent parts of our world, and understanding them empowers us to make informed decisions.
Latest Posts
Latest Posts
-
What Is The Difference Between Median And Mean
Nov 21, 2025
-
How To Multiply Whole Numbers And Decimals
Nov 21, 2025
-
Distinguish Between An Insulator And A Conductor
Nov 21, 2025
-
How Many Bonds Does Boron Make
Nov 21, 2025
-
Is 1 2 Greater Than 3 8
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about Is 1 2 Greater Than 3 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.