8 Is What Percent Of 12
pinupcasinoyukle
Nov 21, 2025 · 9 min read
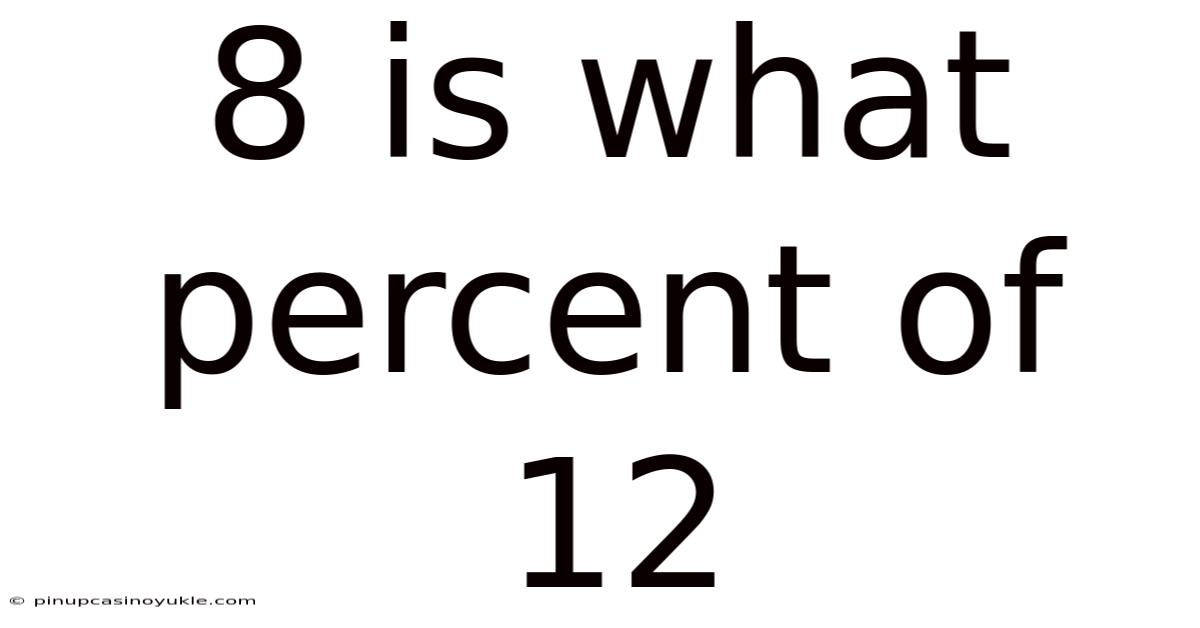
Table of Contents
Calculating percentages is a fundamental skill applicable in numerous aspects of daily life, from figuring out discounts at the store to understanding statistical data. Determining what percentage a number represents of another is a common task. In this article, we will explore how to calculate what percentage 8 is of 12, providing a clear, step-by-step guide and addressing common questions to ensure a comprehensive understanding.
Understanding Percentages
Before diving into the specific calculation, it's essential to grasp the basics of percentages. A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin "per centum," meaning "out of one hundred." When we say "X percent," we mean X out of every 100. For example, 50% means 50 out of 100, or half.
Percentages are used to express:
- Ratios
- Changes
- Comparisons
They provide a standardized way to understand the relative size of numbers.
The Basic Formula
The fundamental formula for calculating what percentage one number is of another is:
(Part / Whole) * 100 = Percentage
Where:
- Part is the number you want to express as a percentage.
- Whole is the total or reference number.
- Percentage is the result you're looking for, expressed as a percentage.
Step-by-Step Calculation: 8 is What Percent of 12?
Now, let's apply this formula to our specific problem: "8 is what percent of 12?"
Step 1: Identify the 'Part' and the 'Whole'
In this question:
- The Part is 8 (the number we want to express as a percentage of 12).
- The Whole is 12 (the reference number or the total).
Step 2: Set Up the Equation
Using the formula, we set up the equation as follows:
(8 / 12) * 100 = Percentage
Step 3: Perform the Division
Divide the Part (8) by the Whole (12):
8 / 12 = 0.666666...
This results in a repeating decimal, which we'll use as is for the next step to maintain accuracy.
Step 4: Multiply by 100
Multiply the result of the division by 100 to convert it into a percentage:
0.666666... * 100 = 66.6666...
Step 5: Round to the Desired Precision
Depending on the context, you might want to round the percentage to a certain number of decimal places. For practical purposes, rounding to two decimal places is common:
66.6666... ≈ 66.67%
So, 8 is approximately 66.67% of 12.
Practical Examples
Let's consider some real-world examples where this calculation might be useful:
-
Test Scores: Suppose you scored 8 out of 12 on a quiz. To find out your percentage score:
(8 / 12) * 100 = 66.67%You scored approximately 66.67% on the quiz. -
Budgeting: Imagine you've allocated $12 for entertainment, and you've spent $8. To find out what percentage of your entertainment budget you've used:
(8 / 12) * 100 = 66.67%You've spent approximately 66.67% of your entertainment budget. -
Inventory: A store has 12 items in stock, and 8 have been sold. To find out the percentage of items sold:
(8 / 12) * 100 = 66.67%Approximately 66.67% of the items have been sold.
Understanding the Result
The result, 66.67%, means that 8 represents about two-thirds of 12. Understanding this relationship is crucial in various applications, providing a clear understanding of proportional relationships.
Alternative Methods for Calculation
While the formula (Part / Whole) * 100 is the most straightforward, there are alternative methods you can use to calculate percentages.
1. Using Fractions
You can simplify the fraction before converting it to a percentage:
- Start with the fraction
8/12. - Simplify the fraction by dividing both the numerator (8) and the denominator (12) by their greatest common divisor (GCD), which is 4.
8 ÷ 4 = 2and12 ÷ 4 = 3, so the simplified fraction is2/3.- Convert the simplified fraction to a percentage:
(2/3) * 100 = 66.67%.
2. Using Proportions
Setting up a proportion can also help calculate the percentage. A proportion is an equation that states that two ratios are equal. In this case, we can set up the proportion:
8 / 12 = x / 100
Here, x represents the percentage we want to find. To solve for x, cross-multiply:
8 * 100 = 12 * x
800 = 12x
Divide both sides by 12:
x = 800 / 12
x = 66.6666...
Rounding to two decimal places, x ≈ 66.67%.
3. Using Decimal Conversion Directly
Convert the numbers to decimals first and then calculate:
- Divide 8 by 12 to get the decimal:
8 / 12 = 0.666666... - Recognize that this decimal represents the percentage in decimal form.
- Multiply by 100 to convert to percentage:
0.666666... * 100 = 66.67%.
Common Mistakes to Avoid
When calculating percentages, it's easy to make mistakes. Here are some common pitfalls to avoid:
-
Incorrectly Identifying the Part and the Whole: Make sure you know which number is the part (the number you're expressing as a percentage) and which is the whole (the reference number).
-
Forgetting to Multiply by 100: After dividing the part by the whole, you must multiply by 100 to express the result as a percentage.
-
Rounding Too Early: Rounding intermediate results can lead to inaccuracies. It's best to keep as many decimal places as possible until the final step.
-
Misinterpreting the Question: Ensure you understand what the question is asking. For example, "What is 8 percent of 12?" is different from "8 is what percent of 12?"
-
Using the Wrong Formula: Double-check that you are using the correct formula: (Part / Whole) * 100.
Advanced Applications of Percentage Calculations
Understanding how to calculate percentages is not just useful for basic math; it also has advanced applications in various fields:
-
Finance: In finance, percentages are used to calculate interest rates, investment returns, and profit margins. For example, calculating the percentage change in stock prices or determining the annual percentage yield (APY) on a savings account.
-
Statistics: Percentages are used extensively in statistics to represent data and make comparisons. For example, calculating the percentage of respondents who agree with a certain statement in a survey or determining the percentage of error in a statistical model.
-
Retail: Retail businesses use percentages to calculate discounts, markups, and sales tax. Understanding percentage markups helps businesses set prices that cover costs and generate profit.
-
Healthcare: In healthcare, percentages are used to track patient outcomes, calculate medication dosages, and analyze clinical trial data. For example, calculating the percentage of patients who respond positively to a treatment or determining the percentage of a patient's body weight for medication dosage.
-
Education: Educators use percentages to grade assignments, calculate student averages, and analyze performance data. Understanding percentage scores helps educators track student progress and identify areas where students may need additional support.
Tools for Calculating Percentages
While it's essential to understand the manual calculation of percentages, several tools can assist in quick and accurate calculations:
-
Calculators: Standard calculators have a percentage function that simplifies the calculation. Simply enter the part, divide by the whole, and press the percentage button.
-
Spreadsheet Software: Programs like Microsoft Excel and Google Sheets can perform percentage calculations using formulas. For example, you can enter
=A1/B1*100in a cell to calculate the percentage if A1 contains the part and B1 contains the whole. -
Online Percentage Calculators: Numerous websites offer free percentage calculators. These tools typically require you to enter the part and the whole, and they will calculate the percentage instantly.
-
Mobile Apps: Many mobile apps are designed to perform various calculations, including percentages. These apps can be convenient for quick calculations on the go.
Examples of Percentage Increase and Decrease
In addition to calculating what percentage one number is of another, understanding percentage increase and decrease is crucial.
Percentage Increase
Percentage increase is the percentage by which a quantity has increased. The formula for percentage increase is:
[(New Value - Original Value) / Original Value] * 100 = Percentage Increase
Example: If a price increases from $12 to $15, the percentage increase is:
[($15 - $12) / $12] * 100 = (3 / 12) * 100 = 25%
The price increased by 25%.
Percentage Decrease
Percentage decrease is the percentage by which a quantity has decreased. The formula for percentage decrease is:
[(Original Value - New Value) / Original Value] * 100 = Percentage Decrease
Example: If a price decreases from $12 to $9, the percentage decrease is:
[($12 - $9) / $12] * 100 = (3 / 12) * 100 = 25%
The price decreased by 25%.
Percentages in Everyday Life
Percentages are ubiquitous in daily life. Here are some more examples of how percentages are used:
-
Discounts: When shopping, discounts are often expressed as percentages. For example, a 20% discount on a $50 item means you save $10.
-
Interest Rates: Interest rates on loans and savings accounts are expressed as percentages. Understanding these rates is crucial for making informed financial decisions.
-
Nutrition: Food labels often list the percentage of daily values for nutrients. This helps you understand how much of each nutrient you're consuming relative to the recommended daily intake.
-
Surveys: Survey results are often presented as percentages. For example, a poll might show that 60% of respondents support a particular policy.
-
Weather: The probability of rain is often expressed as a percentage. For example, a 30% chance of rain means there is a 30% likelihood of rain in a particular area.
Tips for Improving Accuracy in Percentage Calculations
To ensure accurate percentage calculations, consider the following tips:
-
Double-Check Your Numbers: Before performing any calculations, double-check that you have the correct values for the part and the whole.
-
Use a Calculator: When dealing with complex numbers or multiple steps, use a calculator to minimize errors.
-
Show Your Work: Writing down each step of the calculation can help you identify and correct any mistakes.
-
Understand the Context: Ensure you understand the context of the problem and what the question is asking.
-
Practice Regularly: Like any skill, calculating percentages becomes easier with practice. Regularly practice percentage calculations to improve your accuracy and speed.
Conclusion
Calculating what percentage 8 is of 12 involves understanding the fundamental principles of percentages and applying a simple formula: (Part / Whole) * 100. By following the step-by-step guide outlined in this article, you can accurately determine that 8 is approximately 66.67% of 12. This skill is not only valuable for academic purposes but also has numerous practical applications in everyday life, from budgeting and shopping to understanding statistics and finance. By avoiding common mistakes and using the tools and techniques described, you can master percentage calculations and confidently apply them in various contexts.
Latest Posts
Latest Posts
-
What Is An Independent And Dependent Clause
Nov 21, 2025
-
Negative Minus A Negative Is What
Nov 21, 2025
-
8 Is What Percent Of 12
Nov 21, 2025
-
Are 6 9 And 4 6 Equivalent
Nov 21, 2025
-
Standard Deviation Of Binomial Distribution Formula
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about 8 Is What Percent Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.