11 Is What Percent Of 12
pinupcasinoyukle
Nov 05, 2025 · 10 min read
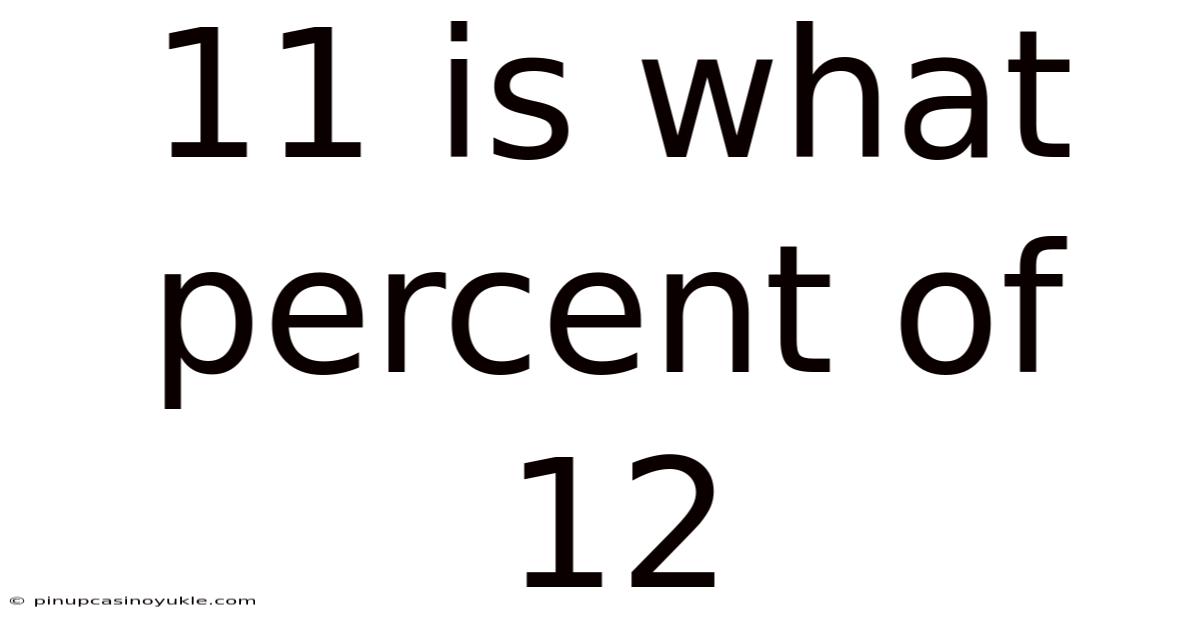
Table of Contents
Finding percentages can be a tricky skill, but once mastered, it becomes an invaluable tool for everyday life, from calculating discounts to understanding statistics. Understanding that 11 is what percent of 12 is a common question that requires a clear, step-by-step approach. This article will guide you through the process, ensuring you grasp not just the solution, but also the underlying concepts.
Understanding the Basics
Before we dive into solving the problem of determining what percentage 11 represents of 12, it's crucial to understand the fundamental concepts of percentages. A percentage is essentially a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin "per centum," which means "out of one hundred." This is why percentages are always relative to a base of 100. Understanding this basic principle makes the calculation process much more intuitive.
What is a Percentage?
A percentage is a ratio that compares a number to 100. It's a way to express a part of a whole. For example, if you have 50%, it means 50 out of 100, or half of the total. Percentages are commonly used in various real-world scenarios such as calculating discounts, interest rates, and grades. The symbol "%" is used to denote percentage.
Key Terms
To effectively work with percentages, it’s important to be familiar with a few key terms:
- Base: The total or whole amount. In the question "11 is what percent of 12," 12 is the base.
- Part: The portion of the whole that you're interested in. In this case, 11 is the part.
- Percentage: The ratio of the part to the base, expressed as a value out of 100. This is what we want to find.
Step-by-Step Calculation
Now, let’s break down how to calculate what percentage 11 is of 12. The method is straightforward and can be applied to any similar percentage problem.
Step 1: Set Up the Equation
The first step is to set up the equation correctly. The general formula to find what percent one number is of another is:
(Part / Base) = (Percentage / 100)
In our case, the part is 11 and the base is 12. So, the equation becomes:
(11 / 12) = (Percentage / 100)
Step 2: Solve for the Percentage
To solve for the percentage, we need to isolate the "Percentage" variable. We can do this by multiplying both sides of the equation by 100:
(11 / 12) * 100 = Percentage
Step 3: Perform the Calculation
Now, perform the calculation:
-
Divide 11 by 12:
11 / 12 = 0.916666... -
Multiply the result by 100:
0. 916666... * 100 = 91.6666...
Step 4: Round the Result
The result is a repeating decimal. Depending on the level of precision required, you can round the percentage to a certain number of decimal places. For example, rounding to two decimal places gives:
91.67%
Therefore, 11 is approximately 91.67% of 12.
Alternative Method: Direct Formula
An alternative, more direct method involves using the formula:
Percentage = (Part / Base) * 100
Using this formula directly:
Percentage = (11 / 12) * 100
This simplifies the process and gets you to the same result more quickly.
Example Using the Direct Formula
Let's apply this direct formula:
Percentage = (11 / 12) * 100
Percentage = 0.916666... * 100
Percentage = 91.6666...
Rounded to two decimal places:
Percentage ≈ 91.67%
Understanding the Result
Now that we've calculated that 11 is approximately 91.67% of 12, it's important to understand what this means in practical terms. This percentage tells us that 11 represents a significant portion of 12, nearly the whole amount. In other words, 11 is very close to being the same value as 12.
Practical Interpretations
Understanding percentages can be very useful in a variety of contexts. Here are a few examples of how this specific calculation might be applied:
- Test Scores: If a student scores 11 out of 12 on a test, their score is approximately 91.67%. This is a high score, indicating a strong understanding of the material.
- Goal Achievement: If you've completed 11 out of 12 tasks in a project, you've accomplished approximately 91.67% of the project. This shows that you are very close to finishing.
- Inventory Levels: If a store has 11 units of a product in stock out of an initial 12, they have approximately 91.67% of their initial stock remaining.
Common Mistakes to Avoid
When calculating percentages, there are several common mistakes that people often make. Being aware of these pitfalls can help ensure accurate results.
Misidentifying the Base and Part
One of the most common errors is confusing the base and the part. Always make sure you correctly identify which number represents the whole (the base) and which number represents the portion of the whole (the part). In the question "11 is what percent of 12," 12 is the base because it represents the total amount, and 11 is the part because it represents a portion of that total.
Incorrectly Setting Up the Equation
Another frequent mistake is setting up the equation incorrectly. The correct formula is:
(Part / Base) = (Percentage / 100)
Ensure that you place the numbers in the correct positions in the equation.
Arithmetic Errors
Simple arithmetic errors can also lead to incorrect percentages. Double-check your calculations, especially when dividing and multiplying. Using a calculator can help reduce the likelihood of these errors.
Rounding Too Early
Rounding numbers too early in the calculation can also affect the accuracy of the final result. It's generally best to perform the calculations with as many decimal places as possible and then round the final percentage to the desired level of precision.
Examples of Percentage Calculations
To solidify your understanding, let’s look at a few more examples of percentage calculations.
Example 1: 15 is what percent of 20?
-
Identify the Part and Base:
- Part = 15
- Base = 20
-
Set Up the Equation:
(15 / 20) = (Percentage / 100) -
Solve for the Percentage:
Percentage = (15 / 20) * 100 -
Perform the Calculation:
15 / 20 = 0.750.75 * 100 = 75
Therefore, 15 is 75% of 20.
Example 2: 8 is what percent of 25?
-
Identify the Part and Base:
- Part = 8
- Base = 25
-
Set Up the Equation:
(8 / 25) = (Percentage / 100) -
Solve for the Percentage:
Percentage = (8 / 25) * 100 -
Perform the Calculation:
8 / 25 = 0.320.32 * 100 = 32
Therefore, 8 is 32% of 25.
Example 3: 45 is what percent of 50?
-
Identify the Part and Base:
- Part = 45
- Base = 50
-
Set Up the Equation:
(45 / 50) = (Percentage / 100) -
Solve for the Percentage:
Percentage = (45 / 50) * 100 -
Perform the Calculation:
45 / 50 = 0.90.9 * 100 = 90
Therefore, 45 is 90% of 50.
Advanced Tips and Tricks
For those looking to enhance their percentage calculation skills, here are some advanced tips and tricks that can be helpful.
Mental Math Techniques
Developing mental math skills can make calculating percentages quicker and easier, especially in everyday situations where a calculator might not be available.
- Finding 10%: To find 10% of a number, simply move the decimal point one place to the left. For example, 10% of 120 is 12.
- Finding 1%: To find 1% of a number, move the decimal point two places to the left. For example, 1% of 120 is 1.2.
- Combining Percentages: Use these techniques to find other percentages. For example, to find 20% of 120, calculate 10% (12) and then multiply by 2 (12 * 2 = 24).
Using Benchmarks
Using benchmark percentages can help you estimate percentages quickly. Common benchmarks include 10%, 25%, 50%, and 75%. For example, if you need to find approximately what percentage 30 is of 60, you can recognize that 30 is half of 60, so it's 50%.
Percentage Increase and Decrease
Understanding percentage increase and decrease is also important. The formulas are:
- Percentage Increase:
((New Value - Old Value) / Old Value) * 100 - Percentage Decrease:
((Old Value - New Value) / Old Value) * 100
For example, if a price increases from $20 to $25, the percentage increase is (($25 - $20) / $20) * 100 = 25%.
Real-World Applications
Percentages are used extensively in everyday life. Here are a few real-world scenarios where understanding percentages is essential.
Finance
In finance, percentages are used to calculate interest rates, investment returns, and loan payments. Understanding percentages can help you make informed decisions about your finances.
Retail
Retailers use percentages to calculate discounts, sales tax, and profit margins. Knowing how to calculate percentages can help you determine whether you're getting a good deal when shopping.
Health
In healthcare, percentages are used to express the effectiveness of treatments, the risk of diseases, and the composition of nutrients in food.
Education
In education, percentages are used to calculate grades and assess student performance. Understanding percentages is crucial for students and educators alike.
Utilizing Online Tools
In today's digital age, numerous online tools and calculators are available to assist with percentage calculations. These tools can save time and reduce the risk of errors, especially when dealing with complex calculations.
Online Percentage Calculators
Online percentage calculators are readily accessible and easy to use. Simply enter the part and the base, and the calculator will instantly provide the percentage. These calculators often offer additional features, such as calculating percentage increase, percentage decrease, and the difference between two percentages.
Spreadsheet Software
Spreadsheet software like Microsoft Excel and Google Sheets can also be used to perform percentage calculations. These tools offer a wide range of functions and formulas that make it easy to calculate percentages and perform more complex statistical analyses.
Mobile Apps
Numerous mobile apps are designed to help with percentage calculations. These apps are convenient for on-the-go calculations and often include features such as history tracking and the ability to save frequently used calculations.
Common FAQs About Percentage Calculations
To further clarify any remaining questions, here are some frequently asked questions about percentage calculations.
Q: How do I convert a fraction to a percentage?
A: To convert a fraction to a percentage, divide the numerator by the denominator and then multiply by 100. For example, to convert 3/4 to a percentage:
(3 / 4) * 100 = 75%
Q: How do I convert a decimal to a percentage?
A: To convert a decimal to a percentage, multiply the decimal by 100. For example, to convert 0.65 to a percentage:
0.65 * 100 = 65%
Q: How do I find the original value if I know the percentage and the part?
A: To find the original value (base), use the formula:
Base = Part / (Percentage / 100)
For example, if 20% of a number is 40, the original number is:
Base = 40 / (20 / 100) = 200
Q: How do I calculate percentage change?
A: To calculate percentage change, use the formula:
Percentage Change = ((New Value - Old Value) / Old Value) * 100
If the result is positive, it's a percentage increase. If the result is negative, it's a percentage decrease.
Conclusion
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life. By understanding the basic principles, following the step-by-step methods, and avoiding common mistakes, you can confidently tackle any percentage problem. Whether you're calculating discounts at the store, analyzing financial data, or simply trying to understand statistics, a solid grasp of percentages is an invaluable asset. So, the next time you're faced with the question of 11 is what percent of 12 or any similar problem, you'll have the knowledge and skills to solve it accurately and efficiently.
Latest Posts
Latest Posts
-
How To Research And Explore An Alternating Series
Nov 05, 2025
-
Two To The Power Of Zero
Nov 05, 2025
-
How To Calculate P Value From Z Score
Nov 05, 2025
-
Negative Number Minus A Negative Number
Nov 05, 2025
-
Time Is Change In Velocity Divided By A
Nov 05, 2025
Related Post
Thank you for visiting our website which covers about 11 Is What Percent Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.