Negative Number Minus A Negative Number
pinupcasinoyukle
Nov 05, 2025 · 8 min read
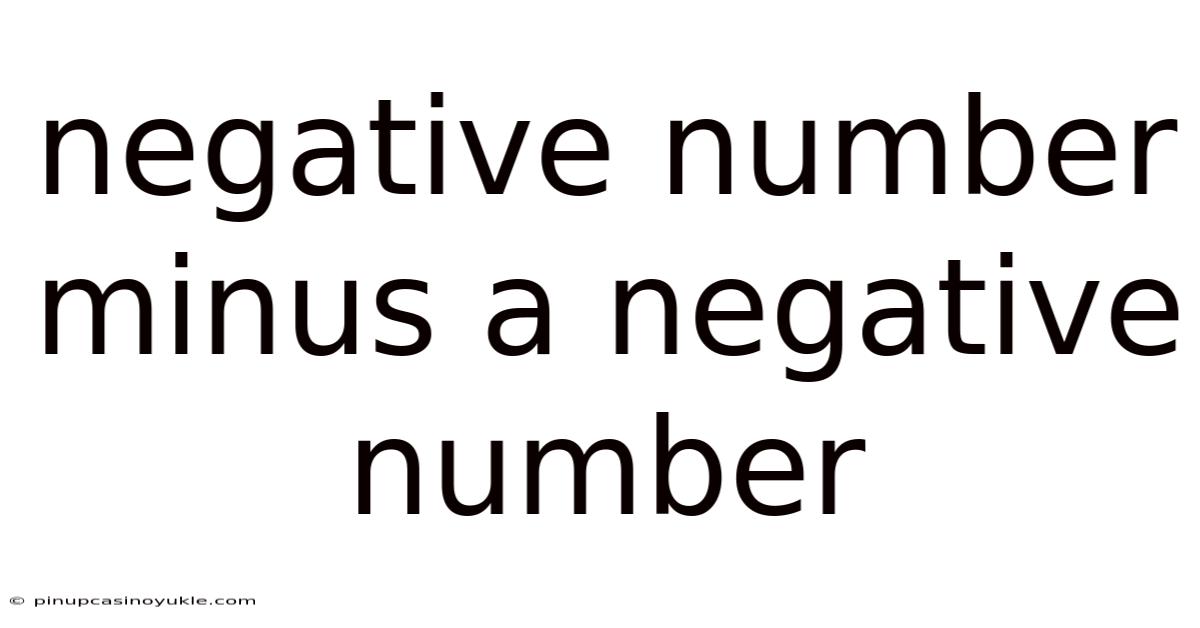
Table of Contents
The seemingly simple act of subtracting a negative number from another negative number opens a doorway into the fascinating world of number theory and mathematical operations. It's a concept that often causes confusion for those new to mathematics, but with a clear understanding of the underlying principles, it becomes a straightforward and even intuitive process. This article aims to demystify the subtraction of negative numbers, providing a comprehensive explanation suitable for learners of all levels. We will delve into the rules, explore practical examples, and even touch upon the underlying mathematical rationale behind this operation.
Understanding Negative Numbers
Before tackling subtraction, let's solidify our understanding of negative numbers themselves. Negative numbers represent values less than zero. They are commonly used to represent concepts like:
- Debt: Owing money is a classic example. If you owe $50, you have -$50.
- Temperature: Temperatures below zero degrees Celsius or Fahrenheit are negative.
- Elevation: Depths below sea level are often represented as negative values.
- Directions: Moving backward or in a direction opposite to a defined positive direction.
The number line is an invaluable tool for visualizing negative numbers. Zero sits at the center, positive numbers extend to the right, and negative numbers extend to the left. The further a negative number is from zero, the smaller its value. For instance, -10 is smaller than -2.
The Subtraction Operation: A Quick Review
Subtraction, at its core, is the process of finding the difference between two numbers. When we subtract a number b from a number a, written as a - b, we are essentially asking: "What value, when added to b, gives us a?"
For example, 7 - 3 = 4 because 4 + 3 = 7. Subtraction can be visualized on the number line as moving to the left from the starting number (a) by the value being subtracted (b).
The Golden Rule: Subtracting a Negative is Adding a Positive
This is the fundamental rule that governs subtracting a negative number. It states:
Subtracting a negative number is equivalent to adding its positive counterpart.
Mathematically, this can be expressed as:
a - (-b) = a + b
This rule may seem counterintuitive at first, but we'll explore the reasoning behind it shortly. For now, let's focus on applying the rule.
Applying the Rule: Step-by-Step Examples
Let's work through some examples to illustrate how to subtract a negative number from another negative number.
Example 1: -5 - (-3)
- Identify the operation: We are subtracting -3 from -5.
- Apply the rule: -5 - (-3) becomes -5 + 3
- Perform the addition: -5 + 3 = -2
- Think of this as having a debt of $5 and then gaining $3. You still have a debt, but it's reduced to $2.
- On the number line, start at -5 and move 3 units to the right (because you are adding).
Example 2: -12 - (-8)
- Identify the operation: We are subtracting -8 from -12.
- Apply the rule: -12 - (-8) becomes -12 + 8
- Perform the addition: -12 + 8 = -4
- Imagine owing $12 and then receiving $8. You still owe $4.
- On the number line, start at -12 and move 8 units to the right.
Example 3: -2 - (-10)
- Identify the operation: We are subtracting -10 from -2.
- Apply the rule: -2 - (-10) becomes -2 + 10
- Perform the addition: -2 + 10 = 8
- You owe $2, but then you receive $10. You now have $8.
- Start at -2 on the number line and move 10 units to the right. This lands you on positive 8.
Example 4: -1 - (-1)
- Identify the operation: We are subtracting -1 from -1.
- Apply the rule: -1 - (-1) becomes -1 + 1
- Perform the addition: -1 + 1 = 0
- You owe $1 and receive $1. You now have $0.
- Starting at -1 and moving one unit to the right lands you on zero.
General Procedure:
When faced with subtracting a negative number:
- Rewrite the expression: Replace the subtraction of the negative with the addition of the positive.
a - (-b)becomesa + b. - Evaluate the resulting expression: Apply the rules of addition for signed numbers.
- If the signs are the same (both positive or both negative), add the absolute values and keep the sign.
- If the signs are different, subtract the smaller absolute value from the larger absolute value and keep the sign of the number with the larger absolute value.
Why Does Subtracting a Negative Work? The Mathematical Explanation
The seemingly strange rule of "subtracting a negative is adding a positive" is deeply rooted in mathematical principles. Here are a few ways to understand the rationale:
-
Additive Inverse: Every number has an additive inverse (also known as the opposite). The additive inverse of a number a is the number that, when added to a, results in zero. For example, the additive inverse of 5 is -5, and the additive inverse of -3 is 3. Subtraction can be defined as adding the additive inverse: a - b is the same as a + (-b). Therefore, a - (-b) is the same as a + (-(-b)). Since the additive inverse of -b is b, then a - (-b) simplifies to a + b.
-
Number Line Reasoning: Imagine you are standing on the number line at -5. Subtracting 3 would mean moving 3 units to the left, ending up at -8. Now, imagine subtracting -3. Subtracting a negative can be thought of as the opposite of subtracting a positive. Instead of moving left, you move to the right, the opposite direction. So, subtracting -3 from -5 means moving 3 units to the right from -5, landing you at -2.
-
Pattern Recognition: Consider the following pattern:
5 - 3 = 2 5 - 2 = 3 5 - 1 = 4 5 - 0 = 5 5 - (-1) = 6 5 - (-2) = 7 5 - (-3) = 8
As you subtract smaller and smaller numbers from 5, the result increases. Subtracting negative numbers continues this trend, effectively adding to the original number.
-
Maintaining Consistency: The rule a - (-b) = a + b maintains consistency with other mathematical rules and properties. If we didn't define subtracting a negative in this way, it would lead to contradictions and inconsistencies within the mathematical system.
Common Mistakes to Avoid
-
Confusing the Signs: One common mistake is to incorrectly apply the rule or to confuse the signs. Carefully rewrite the expression before performing any calculations. Double-check that you have correctly changed the subtraction of a negative to the addition of a positive.
-
Misunderstanding the Number Line: Visualize the number line when adding or subtracting negative numbers. Moving to the right represents addition (or subtracting a negative), and moving to the left represents subtraction.
-
Ignoring the Order of Operations: Remember the order of operations (PEMDAS/BODMAS). If there are multiple operations in an expression, perform them in the correct order. In the case of a series of additions and subtractions, work from left to right.
Real-World Applications
While subtracting negative numbers might seem like an abstract concept, it has practical applications in various real-world scenarios:
- Finance: Calculating profit and loss, especially when dealing with debts and credits.
- Science: Determining temperature changes, particularly in situations where temperatures drop below zero. Calculating changes in elevation below sea level.
- Engineering: Analyzing circuits with positive and negative currents or voltages.
- Computer Science: Representing data and performing calculations in programming.
Advanced Concepts
Once you've mastered the basics, you can explore more advanced concepts involving negative numbers and subtraction:
- Subtracting Negative Numbers in Algebra: The same rules apply when working with variables. For example, x - (-y) = x + y.
- Subtracting Negative Numbers in Complex Equations: Be mindful of the order of operations and the proper application of the rules for signed numbers when solving complex equations.
- Relationship to Other Operations: Understand how subtracting negative numbers relates to other mathematical operations like multiplication and division of negative numbers.
FAQs: Answering Your Questions
-
Why does subtracting a negative number turn into addition? It's because subtracting a negative is the same as adding the additive inverse (opposite) of the negative number.
-
Is subtracting a negative always the same as adding a positive? Yes, a - (-b) is always equal to a + b. This is a fundamental rule in mathematics.
-
What if I have multiple negative signs in a row? Simplify the expression step-by-step, applying the rule a - (-b) = a + b to each pair of consecutive negative signs. For example,
5 - (-2) - (-3)becomes5 + 2 + 3 = 10. -
Does this rule only apply to integers? No, the rule applies to all real numbers, including fractions, decimals, and irrational numbers.
-
How can I best remember this rule? Think of it as "two negatives make a positive." Or, visualize the number line and remember that subtracting a negative means moving to the right.
Conclusion: Mastering the Subtraction of Negative Numbers
Subtracting negative numbers doesn't have to be a source of confusion. By understanding the fundamental rule (subtracting a negative is adding a positive), practicing with examples, and grasping the underlying mathematical principles, you can confidently perform this operation. Remember to visualize the number line, avoid common mistakes, and relate the concept to real-world applications to solidify your understanding. With consistent practice, you'll master the subtraction of negative numbers and unlock new levels of mathematical proficiency. So, embrace the negatives, apply the rules, and watch your mathematical skills soar!
Latest Posts
Latest Posts
-
Whats The Difference Between A Plant And Animal Cell
Nov 05, 2025
-
Solve By Taking The Square Root
Nov 05, 2025
-
How To Find Mean In Binomial Distribution
Nov 05, 2025
-
Can A Negative Be A Whole Number
Nov 05, 2025
-
What Is The Unit Of Measurement For Volume
Nov 05, 2025
Related Post
Thank you for visiting our website which covers about Negative Number Minus A Negative Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.