What Percentage Of 150 Equals 90
pinupcasinoyukle
Nov 12, 2025 · 7 min read
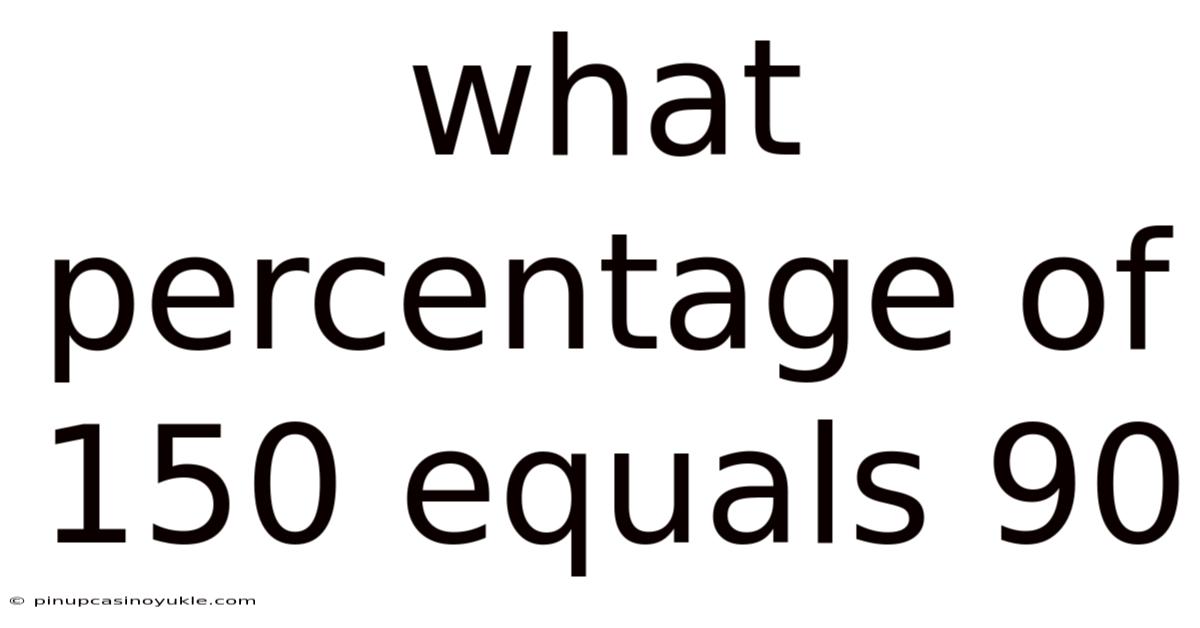
Table of Contents
Calculating percentages is a fundamental skill applicable across various fields, from finance and statistics to everyday shopping scenarios. Understanding how to determine what percentage one number represents of another is crucial for making informed decisions and interpreting data accurately. In this context, we'll explore how to calculate what percentage of 150 equals 90. This involves understanding the basic formula for percentage calculations and applying it to this specific problem.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. In simpler terms, it tells you how much of something you have out of a whole when that whole is divided into 100 parts. The word "percent" comes from the Latin "per centum," meaning "out of one hundred."
Percentages are used to express:
- Ratios: Comparing one quantity to another.
- Changes: Indicating increases or decreases in a value over time.
- Distributions: Showing how a total amount is divided into different parts.
The Basic Percentage Formula
The fundamental formula to calculate what percentage a number (part) is of another number (whole) is:
Percentage = (Part / Whole) × 100
Where:
- Part is the number you want to express as a percentage.
- Whole is the total or reference number.
Applying the Formula to Our Problem
In our case, we want to find out what percentage of 150 equals 90. Here, 90 is the part, and 150 is the whole. Plugging these values into our formula, we get:
Percentage = (90 / 150) × 100
Let's break down the calculation step-by-step:
-
Divide the part by the whole:
90 / 150 = 0.6
-
Multiply the result by 100:
- 6 × 100 = 60
Therefore, 90 is 60% of 150.
Different Methods to Calculate Percentages
While the formula described above is the most straightforward, there are alternative methods to calculate percentages:
Method 1: Using Ratios and Proportions
This method involves setting up a proportion to find the unknown percentage. A proportion is an equation that states that two ratios are equal. In our case, we can set up the following proportion:
90 / 150 = x / 100
Here, x represents the percentage we are trying to find. To solve for x, we can cross-multiply:
150x = 90 × 100
150x = 9000
Now, divide both sides by 150:
x = 9000 / 150
x = 60
So, 90 is 60% of 150.
Method 2: Using Decimals
This method involves converting the percentage into a decimal and then multiplying it by the whole number. First, we need to express the unknown percentage as a decimal. Let's call it y. Then, we can set up the equation:
150 × y = 90
To solve for y, divide both sides by 150:
y = 90 / 150
y = 0.6
Now, to convert the decimal 0.6 into a percentage, multiply by 100:
Percentage = 0.6 × 100 = 60%
Method 3: Using Fractions
This method involves expressing the percentage as a fraction. We already have the fraction 90/150, which represents the ratio of the part to the whole. To convert this fraction into a percentage, we need to express it as an equivalent fraction with a denominator of 100.
First, simplify the fraction 90/150:
90/150 = 3/5
Now, convert 3/5 into an equivalent fraction with a denominator of 100:
(3/5) × (20/20) = 60/100
The fraction 60/100 directly translates to 60%.
Real-World Applications
Understanding how to calculate percentages is essential in various real-world scenarios:
- Finance: Calculating interest rates, discounts, taxes, and investment returns.
- Retail: Determining sale prices, markups, and profit margins.
- Statistics: Analyzing data, interpreting survey results, and understanding statistical distributions.
- Health: Calculating body fat percentage, medication dosages, and nutritional information.
- Education: Grading assignments, tracking student progress, and comparing performance metrics.
- Everyday Life: Calculating tips, splitting bills, and understanding discounts while shopping.
Common Mistakes to Avoid
When calculating percentages, it's important to avoid these common mistakes:
-
Misidentifying the Part and the Whole: Confusing the part and the whole can lead to incorrect calculations. Always ensure you correctly identify which number represents the portion you are interested in and which number represents the total.
-
Forgetting to Multiply by 100: The formula requires you to multiply the result of the division by 100 to express the value as a percentage. Forgetting this step will give you a decimal value instead of a percentage.
-
Incorrectly Converting Decimals and Fractions: Make sure you accurately convert decimals and fractions into percentages by multiplying by 100. Similarly, when converting percentages back to decimals or fractions, divide by 100.
-
Rounding Errors: Rounding numbers prematurely during the calculation can lead to inaccurate results. It is best to perform the entire calculation and then round the final answer to the desired level of precision.
-
Misunderstanding Percentage Increase/Decrease: When calculating percentage increases or decreases, ensure you use the correct base value (original value) to calculate the change. The formula is:
Percentage Change = ((New Value - Original Value) / Original Value) × 100
Advanced Percentage Calculations
Beyond the basics, there are more complex percentage calculations that you might encounter:
Percentage Increase and Decrease
To calculate the percentage increase or decrease between two values, use the following formula:
Percentage Change = ((New Value - Original Value) / Original Value) × 100
- If the result is positive, it indicates a percentage increase.
- If the result is negative, it indicates a percentage decrease.
For example, if a price increases from $100 to $120, the percentage increase is:
Percentage Increase = (($120 - $100) / $100) × 100 = 20%
Calculating Percentage of a Percentage
Sometimes, you need to find the percentage of a percentage. For example, what is 10% of 50% of 200?
-
First, calculate 50% of 200:
50% of 200 = (50/100) × 200 = 100
-
Next, calculate 10% of 100:
10% of 100 = (10/100) × 100 = 10
So, 10% of 50% of 200 is 10.
Working Backwards: Finding the Original Value
Sometimes, you may know the percentage and the resulting value, but you need to find the original value. For example, if 20% of a number is 50, what is the number?
Let the original number be x. We can set up the equation:
20% of x = 50
(20/100) × x = 50
- 2 x = 50
To solve for x, divide both sides by 0.2:
x = 50 / 0.2
x = 250
So, the original number is 250.
Tips for Mastering Percentage Calculations
- Practice Regularly: The more you practice, the more comfortable you will become with percentage calculations. Try solving various problems from different contexts.
- Understand the Concepts: Don't just memorize formulas; understand the underlying concepts. This will help you apply the formulas correctly and solve more complex problems.
- Use Real-World Examples: Relate percentage calculations to real-world scenarios to make them more meaningful. This will also help you remember the formulas and concepts better.
- Double-Check Your Work: Always double-check your calculations to ensure accuracy. Pay attention to detail and avoid common mistakes.
- Use Calculators and Tools: Use calculators or online percentage tools to verify your answers and save time. However, make sure you understand the process and can perform the calculations manually if needed.
Examples and Practice Problems
Let's go through some examples and practice problems to solidify your understanding of percentage calculations:
Example 1: Calculating a Discount
A shirt is priced at $40, and there is a 25% discount. What is the sale price?
-
Calculate the discount amount:
25% of $40 = (25/100) × $40 = $10
-
Subtract the discount from the original price:
$40 - $10 = $30
The sale price of the shirt is $30.
Example 2: Calculating Sales Tax
You buy an item for $50, and the sales tax is 8%. What is the total cost?
-
Calculate the sales tax amount:
8% of $50 = (8/100) × $50 = $4
-
Add the sales tax to the original price:
$50 + $4 = $54
The total cost of the item is $54.
Practice Problem 1
What percentage of 200 is 30?
Solution:
Percentage = (30 / 200) × 100 = 15%
Practice Problem 2
If 15% of a number is 45, what is the number?
Solution:
Let the number be x.
15% of x = 45
(15/100) × x = 45
- 15 x = 45
x = 45 / 0.15 = 300
Conclusion
Calculating percentages is a crucial skill with wide-ranging applications in finance, statistics, and everyday life. By understanding the basic formula and different methods for calculating percentages, you can solve various problems and make informed decisions. Remember to avoid common mistakes, practice regularly, and relate percentage calculations to real-world scenarios to master this essential skill. Whether you're calculating discounts while shopping, analyzing financial data, or understanding statistical results, a solid understanding of percentages will empower you to navigate the world with greater confidence and accuracy.
Latest Posts
Latest Posts
-
What Is Positive Work In Physics
Nov 12, 2025
-
What Is The Properties Of Multiplication
Nov 12, 2025
-
What Is A Unique Property Of Water
Nov 12, 2025
-
Mean Median And Mode Practice Problems
Nov 12, 2025
-
How To Use A Stem And Leaf Plot
Nov 12, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 150 Equals 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.