What Percent Of 60 Is 15
pinupcasinoyukle
Nov 17, 2025 · 8 min read
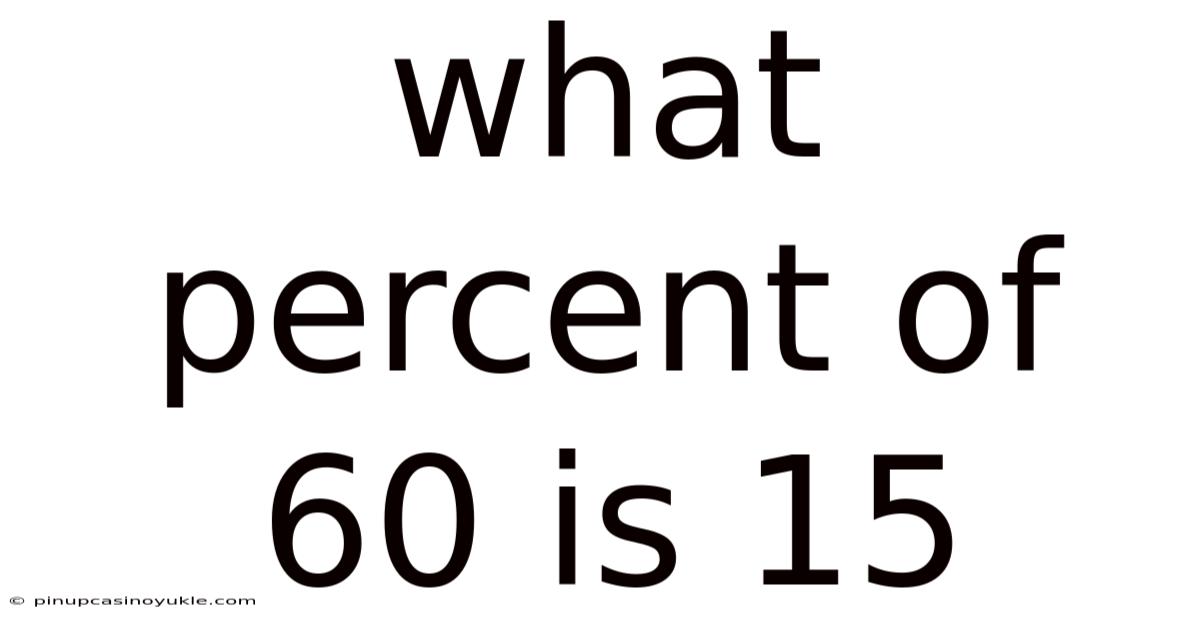
Table of Contents
Finding what percentage one number represents of another is a common mathematical task with practical applications in everyday life, from calculating discounts to understanding statistical data. In this article, we will explore in detail how to determine what percent of 60 is 15, providing a clear explanation, step-by-step instructions, and practical examples to ensure a comprehensive understanding.
Understanding the Basics of Percentages
Before diving into the specific calculation, it's essential to understand what percentages represent. A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin "per centum," meaning "out of one hundred." Therefore, when we say "x percent," we mean x out of every 100.
Percentages are used to express relative changes or relationships between quantities. They simplify comparisons and provide a standardized way to represent proportions. For instance, if a store offers a "20% off" sale, it means that for every $100, you save $20.
The Formula for Calculating Percentages
The fundamental formula to find what percentage a number A is of number B is:
Percentage = (A / B) * 100
Where:
- A is the number that is being expressed as a percentage of another number.
- B is the total or the base number.
- Percentage is the result we want to find, expressed as a percentage.
Step-by-Step Calculation: What Percent of 60 is 15?
Now, let's apply the formula to the specific problem: "What percent of 60 is 15?"
- Identify A and B:
- In this case, A is 15, and B is 60.
- Apply the Formula:
- Plug the values into the formula:
Percentage = (15 / 60) * 100 - Perform the Division:
- Divide 15 by 60:
15 / 60 = 0.25 - Multiply by 100:
- Multiply the result by 100 to convert it into a percentage:
0.25 * 100 = 25 - State the Result:
- Therefore, 15 is 25% of 60.
Detailed Explanation with Examples
To reinforce your understanding, let’s break down the calculation with detailed explanations and additional examples.
Breaking Down the Calculation
The question "What percent of 60 is 15?" is asking us to find the proportion of 15 relative to 60, expressed as a percentage. The formula ( \text{Percentage} = \frac{A}{B} \times 100 ) helps us to quantify this relationship.
- Fraction Form:
- The fraction ( \frac{15}{60} ) represents 15 parts out of 60.
- Decimal Form:
- When we divide 15 by 60, we get 0.25, which is the decimal equivalent of the fraction.
- Percentage Form:
- Multiplying 0.25 by 100 converts the decimal into a percentage, giving us 25%. This means that 15 is 25% of 60.
Example 1: Calculating Discounts
Suppose you want to buy a shirt that originally costs $60, but it is on sale for $15 off. What percentage discount are you getting?
- Identify A and B:
- Here, A is $15 (the discount amount), and B is $60 (the original price).
- Apply the Formula:
Percentage = (15 / 60) * 100 - Perform the Division:
15 / 60 = 0.25 - Multiply by 100:
0.25 * 100 = 25 - Result:
- The discount is 25%.
Example 2: Exam Scores
Imagine you took a test that was worth 60 points, and you scored 15 points. What percentage did you score on the test?
- Identify A and B:
- A is 15 (your score), and B is 60 (the total points).
- Apply the Formula:
Percentage = (15 / 60) * 100 - Perform the Division:
15 / 60 = 0.25 - Multiply by 100:
0.25 * 100 = 25 - Result:
- You scored 25% on the test.
Example 3: Resource Allocation
A company has a budget of $60,000 for a project, and they spend $15,000. What percentage of the budget did they use?
- Identify A and B:
- A is $15,000 (the amount spent), and B is $60,000 (the total budget).
- Apply the Formula:
Percentage = (15000 / 60000) * 100 - Perform the Division:
15000 / 60000 = 0.25 - Multiply by 100:
0.25 * 100 = 25 - Result:
- The company used 25% of their budget.
Common Mistakes to Avoid
When calculating percentages, it's easy to make a few common mistakes. Being aware of these can help you avoid errors.
- Incorrectly Identifying A and B:
- Ensure you correctly identify which number is the part (A) and which is the whole (B). Misidentifying these will lead to an incorrect percentage.
- Forgetting to Multiply by 100:
- The formula requires you to multiply the result of the division by 100 to convert it into a percentage. Forgetting this step will give you the decimal form, not the percentage.
- Rounding Errors:
- If the division results in a long decimal, be mindful of rounding errors. Rounding too early can affect the accuracy of your final percentage.
- Misunderstanding the Question:
- Always read the question carefully to understand what it is asking. Sometimes, the question might be phrased in a way that confuses which number is the part and which is the whole.
Alternative Methods to Calculate Percentages
While the formula ( \text{Percentage} = \frac{A}{B} \times 100 ) is the most straightforward method, there are alternative approaches to calculating percentages that can be useful in certain situations.
Using Proportions
Setting up a proportion is another way to solve percentage problems. A proportion is an equation stating that two ratios are equal.
- Set up the Proportion:
- To find what percent of 60 is 15, you can set up the following proportion:
15 / 60 = x / 100- Here, x represents the percentage we want to find.
- Cross-Multiply:
- Cross-multiply to solve for x:
15 * 100 = 60 * x 1500 = 60x - Solve for x:
- Divide both sides by 60:
x = 1500 / 60 x = 25 - Result:
- Therefore, 15 is 25% of 60.
Mental Math Techniques
For simple calculations, mental math can be a quick way to find percentages. Here are some techniques:
- Finding 10%:
- To find 10% of a number, divide it by 10. For example, 10% of 60 is 6.
- Finding 1%:
- To find 1% of a number, divide it by 100. For example, 1% of 60 is 0.6.
- Combining Percentages:
- You can combine known percentages to find others. For example, to find 25% of 60, you can find 10% (which is 6), multiply it by 2.5 (since 25% is 2.5 times 10%):
6 * 2.5 = 15- Then, calculate the percentage:
(15 / 60) * 100 = 25%
Using a Calculator
A calculator is a handy tool for quickly calculating percentages, especially for more complex numbers.
- Input the Numbers:
- Enter the numbers into the calculator according to the formula:
(15 / 60) * 100 - Calculate:
- Press the equals (=) button to get the result:
25 - Result:
- The calculator will display 25, indicating that 15 is 25% of 60.
Practical Applications in Real Life
Understanding how to calculate percentages is useful in many real-life scenarios. Here are some examples:
- Finance:
- Calculating interest rates on loans or investments.
- Determining the percentage change in stock prices.
- Understanding the impact of taxes on income.
- Retail:
- Calculating discounts and sales prices.
- Determining profit margins.
- Understanding the percentage of sales from different product categories.
- Health and Nutrition:
- Calculating the percentage of daily nutrient intake.
- Determining the percentage of body fat.
- Understanding medication dosages.
- Education:
- Calculating grades and test scores.
- Determining the percentage of students who pass a test.
- Understanding statistics and data analysis.
- Business and Marketing:
- Calculating market share.
- Determining the percentage of successful marketing campaigns.
- Understanding customer demographics.
Advanced Percentage Calculations
While the basic percentage formula is useful, there are more advanced calculations involving percentages that are important to understand.
Percentage Increase
To calculate the percentage increase from an old value to a new value, use the following formula:
Percentage Increase = ((New Value - Old Value) / Old Value) * 100
For example, if a product's price increased from $60 to $75, the percentage increase is:
Percentage Increase = ((75 - 60) / 60) * 100 = (15 / 60) * 100 = 25%
Percentage Decrease
To calculate the percentage decrease from an old value to a new value, use the following formula:
Percentage Decrease = ((Old Value - New Value) / Old Value) * 100
For example, if a product's price decreased from $60 to $45, the percentage decrease is:
Percentage Decrease = ((60 - 45) / 60) * 100 = (15 / 60) * 100 = 25%
Finding the Original Value
Sometimes, you might need to find the original value when you know the final value and the percentage change.
- If the value increased:
- Let the original value be ( x ). If the value increased by ( p )%, then:
New Value = x + (x * (p / 100))- Solve for ( x ) to find the original value.
- If the value decreased:
- Let the original value be ( x ). If the value decreased by ( p )%, then:
New Value = x - (x * (p / 100))- Solve for ( x ) to find the original value.
Conclusion
Understanding how to calculate percentages is a fundamental skill with broad applications in various aspects of life. In this article, we've thoroughly explored how to determine what percent of 60 is 15, breaking down the calculation into simple steps and providing numerous examples to illustrate its practical uses. By mastering the basic formula ( \text{Percentage} = \frac{A}{B} \times 100 ) and avoiding common mistakes, you can confidently tackle percentage-related problems in finance, retail, health, education, and beyond. Additionally, we've discussed alternative methods such as using proportions and mental math techniques, as well as advanced percentage calculations like percentage increase and decrease. With this comprehensive knowledge, you are well-equipped to handle percentage calculations with ease and accuracy.
Latest Posts
Latest Posts
-
Pythagorean Theorem And The Distance Formula
Nov 18, 2025
-
How Many Valence Electrons Do Transition Metals Have
Nov 18, 2025
-
What Cells Are Necessary For Vessel Repair And Clotting
Nov 18, 2025
-
What Is 3 5 1 3
Nov 18, 2025
-
How To Find Mole Of A Compound
Nov 18, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 60 Is 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.