What Percent Is 10 Of 50
pinupcasinoyukle
Nov 08, 2025 · 8 min read
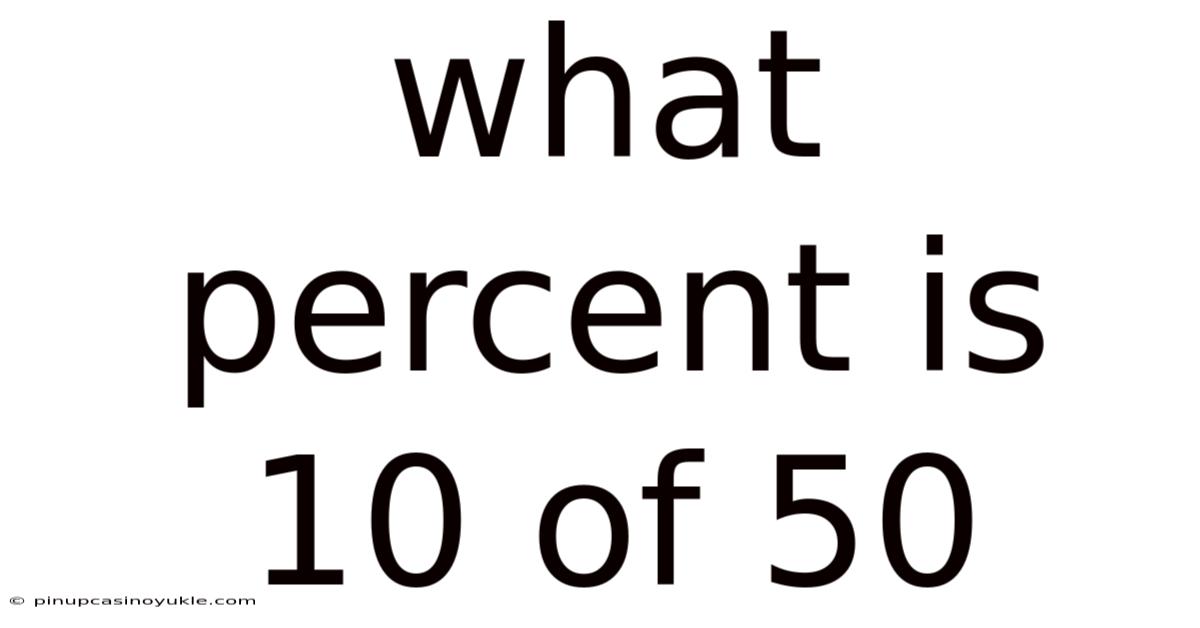
Table of Contents
Calculating percentages is a fundamental skill applicable in various aspects of life, from figuring out discounts while shopping to understanding statistics in reports. When you need to determine "what percent is 10 of 50," you're essentially asking what proportion of 50 is represented by 10, expressed as a percentage. This article will delve into the step-by-step methods to solve this type of problem, provide practical examples, and address common questions to ensure you grasp the concept thoroughly.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin "per centum," meaning "out of one hundred." Using percentages makes it easier to compare different proportions, as they are all standardized to a common base of 100.
Basic Formula for Percentage
The basic formula to calculate a percentage is:
(Part / Whole) × 100 = Percentage
Where:
- Part is the specific amount you are interested in.
- Whole is the total or the reference value.
- Percentage is the result you are trying to find.
Step-by-Step Calculation: What Percent is 10 of 50?
To find out what percent 10 is of 50, follow these steps:
Step 1: Identify the Part and the Whole
In this problem:
- Part = 10
- Whole = 50
Step 2: Apply the Percentage Formula
Using the formula:
(Part / Whole) × 100 = Percentage
Substitute the values:
(10 / 50) × 100 = Percentage
Step 3: Simplify the Fraction
Divide 10 by 50:
10 / 50 = 0.2
Step 4: Multiply by 100
Multiply the result by 100 to convert it to a percentage:
0. 2 × 100 = 20
Therefore, 10 is 20% of 50.
Alternative Method: Using Proportions
Another way to solve this problem is by using proportions. A proportion is an equation stating that two ratios are equal.
Step 1: Set Up the Proportion
Write the proportion as:
10 / 50 = x / 100
Here, x represents the percentage we want to find.
Step 2: Solve for x
To solve for x, cross-multiply:
10 × 100 = 50 × x
1000 = 50x
Step 3: Isolate x
Divide both sides by 50:
1000 / 50 = x
20 = x
So, x = 20, meaning 10 is 20% of 50.
Practical Examples
Let's look at some practical examples where you might need to calculate percentages:
Example 1: Calculating a Discount
Suppose a store is offering a $10 discount on an item originally priced at $50. What is the percentage discount?
- Part (Discount) = $10
- Whole (Original Price) = $50
Using the formula:
(10 / 50) × 100 = 20%
The discount is 20%.
Example 2: Exam Scores
A student scores 10 out of 50 questions correctly on a quiz. What percentage of the questions did the student answer correctly?
- Part (Correct Answers) = 10
- Whole (Total Questions) = 50
Using the formula:
(10 / 50) × 100 = 20%
The student answered 20% of the questions correctly.
Example 3: Budget Allocation
You allocate $10 of your $50 weekly budget to entertainment. What percentage of your budget is allocated to entertainment?
- Part (Entertainment Allocation) = $10
- Whole (Total Budget) = $50
Using the formula:
(10 / 50) × 100 = 20%
20% of your budget is allocated to entertainment.
Common Mistakes to Avoid
When calculating percentages, it’s easy to make a few common mistakes:
Mistake 1: Incorrectly Identifying the Part and Whole
Ensure you correctly identify which number is the part and which is the whole. The part is the specific quantity you're interested in, while the whole is the total or reference value.
Mistake 2: Forgetting to Multiply by 100
After dividing the part by the whole, remember to multiply the result by 100 to convert it into a percentage.
Mistake 3: Misinterpreting the Question
Understand exactly what the question is asking. For example, "What is 10% of 50?" is different from "What percent is 10 of 50?"
Mistake 4: Rounding Errors
When dealing with decimals, be careful with rounding. Rounding too early can lead to inaccuracies in the final percentage.
Advanced Applications of Percentages
Percentages are not just for simple calculations; they are also used in more complex applications.
Percentage Increase and Decrease
To calculate percentage increase or decrease:
- Find the difference between the new value and the original value.
- Divide the difference by the original value.
- Multiply by 100.
Formula:
((New Value - Original Value) / Original Value) × 100 = Percentage Change
Example:
If a price increases from $50 to $60, the percentage increase is:
((60 - 50) / 50) × 100 = (10 / 50) × 100 = 20%
Percentage Composition
Percentage composition is used to describe the relative amount of each element in a compound.
Example:
If you have a solution that is 30 grams of sugar in 150 grams of water, the percentage composition of sugar is:
(30 / (30 + 150)) × 100 = (30 / 180) × 100 ≈ 16.67%
Weighted Averages
In many real-world scenarios, some data points are more significant than others. In these cases, a weighted average is used.
Example: Suppose a student’s final grade is calculated as follows:
- Homework: 20%
- Quizzes: 30%
- Final Exam: 50%
If the student scores 80% on homework, 70% on quizzes, and 90% on the final exam, the weighted average is:
(0.20 × 80) + (0.30 × 70) + (0.50 × 90) = 16 + 21 + 45 = 82%
The Importance of Understanding Percentages
Understanding percentages is crucial for:
- Personal Finance: Calculating interest rates, discounts, and taxes.
- Business: Analyzing sales data, profit margins, and market share.
- Science: Interpreting experimental results and statistical data.
- Everyday Life: Making informed decisions about purchases, health, and more.
Tips for Mastering Percentage Calculations
Here are some tips to help you become more proficient with percentage calculations:
Practice Regularly
The more you practice, the more comfortable you'll become with the calculations. Try solving different types of percentage problems.
Use Real-World Examples
Apply percentage calculations to real-world scenarios to see how they are used in everyday life.
Understand the Underlying Concepts
Don't just memorize formulas; understand the logic behind them. This will help you apply them correctly in different situations.
Use Online Resources
There are many online calculators and tutorials that can help you practice and improve your skills.
Conclusion
Calculating what percent one number is of another is a fundamental skill that has numerous applications in daily life. Whether you're figuring out discounts, understanding statistics, or managing your finances, knowing how to calculate percentages accurately is essential. By understanding the basic formula, practicing with real-world examples, and avoiding common mistakes, you can master this skill and use it to make informed decisions. Remember, practice makes perfect, so keep honing your skills to become more confident and proficient with percentage calculations.
Frequently Asked Questions (FAQ)
Q1: How do I calculate the percentage if I have a decimal?
If you have a decimal result from dividing the part by the whole, simply multiply the decimal by 100 to convert it to a percentage. For example, if Part / Whole = 0.75, then the percentage is 0.75 × 100 = 75%.
Q2: Can a percentage be greater than 100%?
Yes, a percentage can be greater than 100%. This usually happens when you are calculating a percentage increase or comparing a value to a smaller base value. For example, if a value doubles, it represents a 100% increase, and the new value is 200% of the original.
Q3: How do I find the original value if I know the percentage and the part?
To find the original value (whole), use the formula:
Whole = Part / (Percentage / 100)
For example, if 20% of a number is 10, then the whole is:
Whole = 10 / (20 / 100) = 10 / 0.2 = 50
Q4: What is the difference between percentage and percentage points?
Percentage and percentage points are different concepts. A percentage is a ratio expressed as a fraction of 100, while a percentage point is the simple difference between two percentages.
Example:
If an interest rate increases from 10% to 12%, it has increased by 2 percentage points. The percentage increase is:
((12 - 10) / 10) × 100 = 20%
Q5: How can I use a calculator to find percentages?
Most calculators have a percentage function (%). To find what percent 10 is of 50, you can enter:
10 ÷ 50 × 100 =
Or, use the percentage key directly if your calculator has one.
Q6: What are some real-world applications of percentages in business?
In business, percentages are used for:
- Calculating profit margins
- Analyzing sales growth
- Determining market share
- Setting discounts and promotions
- Budgeting and financial planning
Q7: How do I calculate percentage error?
Percentage error is used to determine the difference between an experimental value and a known or accepted value. The formula is:
Percentage Error = (|Experimental Value - Accepted Value| / Accepted Value) × 100
Where |...| denotes absolute value.
Q8: Can I use percentages to compare different sets of data?
Yes, percentages are very useful for comparing different sets of data, especially when the sample sizes are different. By converting data to percentages, you can easily compare proportions and make meaningful conclusions.
Q9: How do I convert a fraction to a percentage?
To convert a fraction to a percentage:
- Divide the numerator by the denominator.
- Multiply the result by 100.
For example, to convert 3/4 to a percentage:
(3 / 4) × 100 = 0.75 × 100 = 75%
Q10: Are there any shortcuts for calculating common percentages?
Yes, here are a few shortcuts for common percentages:
- 50% of a number: Divide the number by 2.
- 25% of a number: Divide the number by 4.
- 10% of a number: Divide the number by 10.
- 1% of a number: Divide the number by 100.
By using these shortcuts, you can quickly estimate percentages without needing a calculator.
Latest Posts
Latest Posts
-
Kwame Nkrumah Definition Ap World History
Nov 08, 2025
-
Osmosis Is Best Defined As The Movement Of
Nov 08, 2025
-
How To Calculate Ph From Molarity
Nov 08, 2025
-
Quadratic Equations Solve By Factoring Worksheet
Nov 08, 2025
-
The Space Between Two Neurons Is Called The
Nov 08, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 10 Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.