What Is The Sqaure Root Of 0
pinupcasinoyukle
Nov 13, 2025 · 7 min read
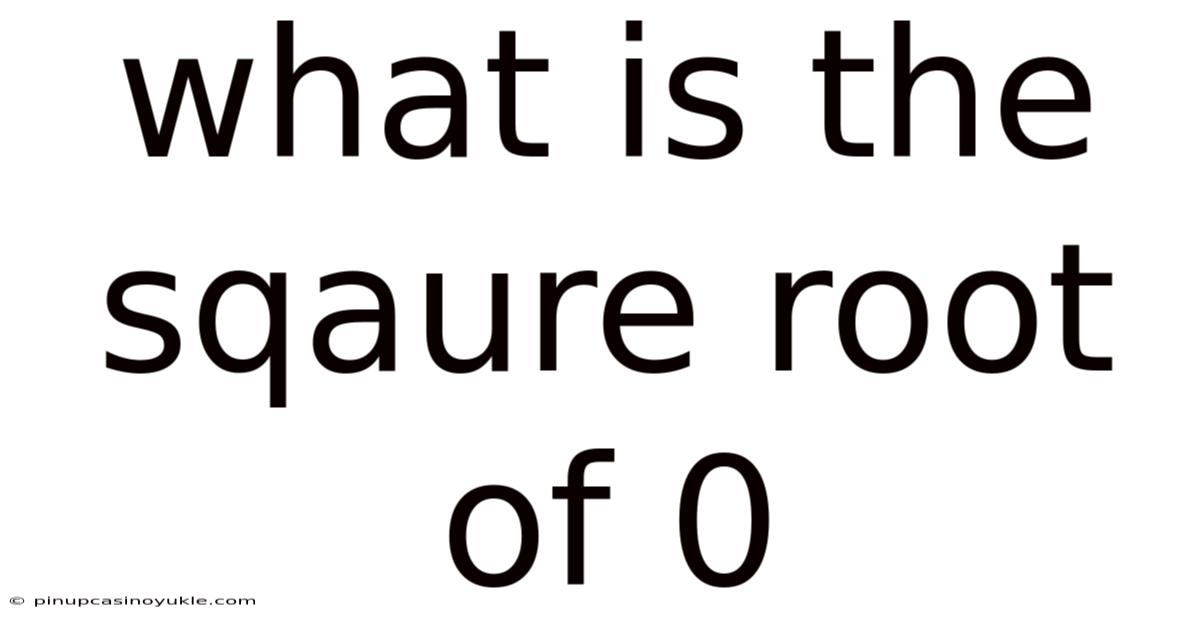
Table of Contents
The square root of 0, a concept that might seem simple at first glance, delves into the core of mathematical principles and opens doors to understanding more complex ideas. It’s more than just a numerical answer; it's a fundamental concept in algebra, calculus, and beyond.
What is a Square Root?
Before diving into the square root of 0 specifically, let's refresh our understanding of what a square root is in general. The square root of a number x is a value y that, when multiplied by itself, equals x. Mathematically, this can be expressed as:
y * y = x
or
y^2 = x
For example, the square root of 9 is 3 because 3 * 3 = 9. Similarly, the square root of 25 is 5 because 5^2 = 25. The concept of a square root extends beyond perfect squares like 9 and 25 to include irrational numbers like the square root of 2 (approximately 1.4142) and complex numbers.
The Square Root of Zero
Now, let's consider the square root of 0. We are looking for a number that, when multiplied by itself, equals 0. In other words, we need to find y such that:
y^2 = 0
The only number that satisfies this condition is 0 itself. Because 0 * 0 = 0, the square root of 0 is 0.
Mathematically, this is represented as:
√0 = 0
This might seem straightforward, but its simplicity belies its importance in various mathematical contexts.
Why is the Square Root of Zero Important?
The square root of zero is crucial for several reasons, spanning across various branches of mathematics:
1. Foundation of Real Numbers:
Zero is a fundamental element of the real number system. Understanding its properties, including its square root, is essential for grasping the nature of real numbers and their operations.
2. Algebraic Equations:
In algebra, the square root of zero often appears when solving equations. For example, consider the quadratic equation:
x^2 = 0
The solution to this equation is x = 0, which is derived from taking the square root of both sides.
3. Calculus and Limits:
In calculus, the square root of zero plays a significant role in the evaluation of limits and continuity of functions. Functions involving square roots often need careful handling around points where the expression inside the square root approaches zero.
4. Mathematical Analysis:
In mathematical analysis, understanding the square root of zero is vital for discussing the behavior of functions near zero, especially when dealing with differentiability and integrability.
5. Computer Science:
In computer science, especially in numerical analysis, algorithms often involve square root calculations. The square root of zero serves as a base case in many algorithms and is essential for handling edge cases correctly.
Properties of Square Roots and Zero
To further appreciate the significance of the square root of zero, let's consider some related properties:
- Non-Negativity: The square root of a non-negative real number is always non-negative. Since zero is non-negative, its square root is also non-negative.
- Uniqueness: The square root of zero is unique; there is only one number that, when multiplied by itself, equals zero.
- Zero Product Property: The zero product property states that if the product of two numbers is zero, then at least one of the numbers must be zero. This property is directly related to the square root of zero.
- Additive Identity: Zero is the additive identity, meaning that adding zero to any number does not change the number. This property, combined with the properties of square roots, highlights the unique role of zero in mathematics.
Complex Numbers and Square Roots
While the square root of zero is straightforward in the realm of real numbers, it's also worth briefly touching upon complex numbers. Complex numbers extend the real number system by including the imaginary unit i, where i is defined as the square root of -1.
In the context of complex numbers, every number (except zero) has two square roots. For example, the square roots of 4 are 2 and -2, because both 2^2 and (-2)^2 equal 4. However, for zero, both square roots are the same: 0.
Practical Applications of the Square Root of Zero
While the concept might seem abstract, the square root of zero has practical applications in various fields:
- Physics: In physics, zero often represents a state of equilibrium or a reference point. For instance, in mechanics, the square root of zero can appear in equations describing the motion of objects, especially when dealing with initial conditions or points of rest.
- Engineering: In engineering, especially in control systems, zero plays a crucial role in determining stability. The square root of zero can arise in the analysis of system responses and stability criteria.
- Computer Graphics: In computer graphics, zero is often used as a coordinate in 3D space or as a component of vectors. The square root of zero can appear in calculations related to distances, transformations, and rendering.
- Statistics: In statistics, zero can represent a baseline or a null hypothesis. The square root of zero might be encountered in calculations related to variance, standard deviation, and statistical testing.
Common Misconceptions
Despite its simplicity, some misconceptions often arise regarding the square root of zero:
- Indeterminate Form: Some might confuse the square root of zero with indeterminate forms like 0/0 or ∞/∞, which appear in calculus when evaluating limits. While these forms require special techniques to resolve, the square root of zero is a well-defined value: 0.
- Division by Zero: The square root of zero is not related to the undefined operation of division by zero. Division by zero is undefined because it violates the fundamental properties of arithmetic.
- Negative Square Roots: While it's true that non-zero positive numbers have two square roots (one positive and one negative), zero has only one square root: zero itself. There is no negative square root of zero, as -0 is the same as 0.
How to Calculate Square Roots
While the square root of zero is straightforward, calculating square roots of other numbers can be more complex. Here are some methods for calculating square roots:
-
Estimation and Approximation:
- For non-perfect squares, you can estimate the square root by finding the nearest perfect squares. For example, to estimate the square root of 10, you know that √9 = 3 and √16 = 4. Since 10 is closer to 9, the square root of 10 will be slightly greater than 3.
- You can refine this estimate by using linear interpolation or other approximation techniques.
-
Babylonian Method (Heron's Method):
- The Babylonian method is an iterative algorithm for approximating the square root of a number x. It starts with an initial guess g and iteratively refines the guess using the formula:
g_(n+1) = (g_n + x/g_n) / 2
- This method converges quickly to the square root of x.
-
Long Division Method:
- The long division method is a manual method for calculating square roots, similar to long division for division. It involves a series of steps to extract the digits of the square root.
-
Calculators and Computers:
- Modern calculators and computers use sophisticated algorithms to calculate square roots quickly and accurately. These algorithms are based on numerical methods like Newton's method or CORDIC algorithms.
The Role of Zero in Mathematics
Zero is a unique and essential number in mathematics. It serves as the additive identity, a placeholder in numerical notation, and a crucial concept in calculus and analysis. Understanding the properties of zero, including its square root, is fundamental to mastering mathematics.
Zero also plays a significant role in various mathematical structures:
- Groups and Rings: In abstract algebra, zero is the additive identity in groups and rings, satisfying the property that a + 0 = a for all elements a.
- Fields: In fields, which are algebraic structures with both addition and multiplication, zero is both the additive identity and has the property that a * 0 = 0 for all elements a.
- Vector Spaces: In linear algebra, the zero vector is the additive identity in vector spaces and plays a crucial role in defining linear combinations and subspaces.
Conclusion
The square root of zero, although seemingly simple, is a fundamental concept in mathematics with far-reaching implications. It is not just a numerical answer but a building block for understanding more complex mathematical ideas, from algebra and calculus to numerical analysis and computer science. Grasping the significance of the square root of zero enhances one's understanding of the properties of numbers and their roles in various mathematical contexts.
Latest Posts
Latest Posts
-
How To Find Volume Of A Rectangular Pyramid
Nov 13, 2025
-
What Is The Difference Between An Ectotherm And An Endotherm
Nov 13, 2025
-
What Are Dependent Clauses And Independent Clauses
Nov 13, 2025
-
The Average Rate Of Change Is
Nov 13, 2025
-
How Do We Describe Transformation In Bacteria
Nov 13, 2025
Related Post
Thank you for visiting our website which covers about What Is The Sqaure Root Of 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.