What Is The Lowest Common Multiple Of 3 And 4
pinupcasinoyukle
Nov 12, 2025 · 10 min read
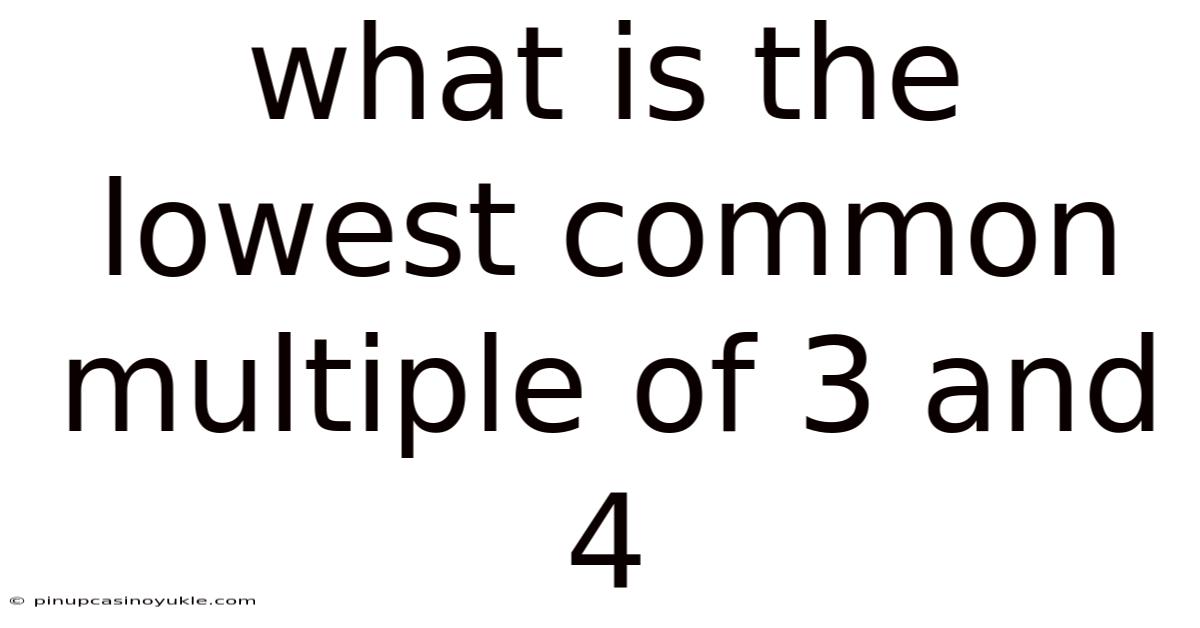
Table of Contents
The lowest common multiple (LCM) of two or more numbers is the smallest positive integer that is perfectly divisible by each of the numbers. When considering 3 and 4, the LCM is the smallest number that both 3 and 4 can divide into without leaving a remainder.
Understanding Multiples
Before diving into how to find the LCM, let's clarify what multiples are. A multiple of a number is the result of multiplying that number by an integer.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, and so on.
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, and so on.
Identifying the Lowest Common Multiple
By examining the lists of multiples for 3 and 4, we can identify common multiples—numbers that appear in both lists. The common multiples of 3 and 4 include 12, 24, 36, and so on. The smallest of these common multiples is 12.
Therefore, the lowest common multiple (LCM) of 3 and 4 is 12.
Methods to Calculate the LCM
There are several methods to calculate the LCM of two or more numbers. Here, we'll explore three common methods: listing multiples, prime factorization, and using the greatest common divisor (GCD).
1. Listing Multiples
As demonstrated earlier, this method involves listing the multiples of each number until a common multiple is found.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, ...
- Multiples of 4: 4, 8, 12, 16, 20, 24, ...
The smallest common multiple in both lists is 12.
This method is straightforward and easy to understand, especially for smaller numbers. However, it can become cumbersome and time-consuming for larger numbers, where the LCM may be significantly larger and require listing many multiples.
2. Prime Factorization
The prime factorization method involves breaking down each number into its prime factors. Prime factors are prime numbers that, when multiplied together, give the original number.
- Prime factorization of 3: 3 (3 is a prime number)
- Prime factorization of 4: 2 x 2 = 2^2
To find the LCM, take the highest power of each prime factor that appears in either factorization and multiply them together.
- The prime factors are 2 and 3.
- The highest power of 2 is 2^2 (from the factorization of 4).
- The highest power of 3 is 3^1 (from the factorization of 3).
LCM (3, 4) = 2^2 x 3 = 4 x 3 = 12
This method is more systematic and efficient for larger numbers because it relies on breaking down the numbers into their fundamental components.
3. Using the Greatest Common Divisor (GCD)
The greatest common divisor (GCD) of two numbers is the largest positive integer that divides both numbers without leaving a remainder. The LCM can be found using the formula:
LCM (a, b) = (|a * b|) / GCD (a, b)
First, find the GCD of 3 and 4. The factors of 3 are 1 and 3. The factors of 4 are 1, 2, and 4. The only common factor is 1, so the GCD of 3 and 4 is 1.
Now, use the formula:
LCM (3, 4) = (|3 * 4|) / GCD (3, 4) = (12) / 1 = 12
This method is particularly useful when the GCD is already known or easily calculated.
Step-by-Step Calculation of LCM(3, 4) Using Prime Factorization
Let's go through the prime factorization method step-by-step to solidify the process.
-
Find the Prime Factorization of Each Number:
- For 3: The prime factorization is simply 3, as 3 is a prime number.
- For 4: The prime factorization is 2 x 2, which can be written as 2^2.
-
Identify All Unique Prime Factors:
- The unique prime factors are 2 and 3.
-
Determine the Highest Power of Each Prime Factor:
- The highest power of 2 is 2^2 (from the prime factorization of 4).
- The highest power of 3 is 3^1 (from the prime factorization of 3).
-
Multiply the Highest Powers of All Unique Prime Factors:
- LCM (3, 4) = 2^2 x 3^1 = 4 x 3 = 12.
Therefore, the LCM of 3 and 4 is 12.
Why is the LCM Important?
The LCM is a fundamental concept in mathematics with numerous practical applications. Understanding and being able to calculate the LCM is essential in various areas, including:
- Fractions: The LCM is used to find a common denominator when adding or subtracting fractions. For example, if you want to add 1/3 and 1/4, you need to find a common denominator, which is the LCM of 3 and 4 (i.e., 12). So, you convert the fractions to 4/12 and 3/12, respectively.
- Time and Scheduling: The LCM is helpful in scheduling events that occur at different intervals. For instance, if one task repeats every 3 days and another repeats every 4 days, the LCM (12) tells you when both tasks will occur on the same day again.
- Algebra: The LCM is used in simplifying algebraic expressions and solving equations, especially when dealing with rational expressions.
- Number Theory: The LCM is a core concept in number theory, helping to explore relationships between numbers and their divisors.
- Real-World Problems: The LCM can be applied to various real-world scenarios, such as determining when two gears will align again or calculating the minimum quantity of items needed to satisfy different grouping requirements.
Practical Examples
Here are a few practical examples to illustrate the use of LCM:
Example 1: Combining Fractions
Suppose you want to add two fractions: 1/3 and 1/4. To do this, you need to find a common denominator. The LCM of 3 and 4 is 12.
- Convert 1/3 to an equivalent fraction with a denominator of 12: (1/3) * (4/4) = 4/12
- Convert 1/4 to an equivalent fraction with a denominator of 12: (1/4) * (3/3) = 3/12
- Now, add the fractions: 4/12 + 3/12 = 7/12
Example 2: Scheduling Tasks
Imagine you have two tasks. Task A needs to be done every 3 days, and Task B needs to be done every 4 days. If both tasks are done today, when will they both need to be done on the same day again?
The LCM of 3 and 4 is 12. This means that both tasks will coincide again in 12 days.
Example 3: Gear Alignment
Two gears are meshed together. Gear A has 3 teeth, and Gear B has 4 teeth. After how many rotations will both gears return to their starting position simultaneously?
The LCM of 3 and 4 is 12. This means Gear A needs to rotate 4 times (12/3) and Gear B needs to rotate 3 times (12/4) for both gears to align back to their original positions.
LCM with More Than Two Numbers
The concept of LCM extends to more than two numbers. To find the LCM of multiple numbers, you can use similar methods as described above, but with some adjustments.
Listing Multiples
This method can be extended to multiple numbers by listing the multiples of each number until a common multiple is found in all lists. However, this can be quite inefficient for more than a few numbers.
Prime Factorization
The prime factorization method is more efficient for finding the LCM of multiple numbers. Here's how it works:
- Find the prime factorization of each number.
- Identify all unique prime factors from all the factorizations.
- Determine the highest power of each prime factor that appears in any of the factorizations.
- Multiply the highest powers of all unique prime factors together.
Example: Find the LCM of 3, 4, and 6.
- Prime factorizations:
- 3 = 3
- 4 = 2^2
- 6 = 2 x 3
- Unique prime factors: 2 and 3
- Highest powers:
- Highest power of 2: 2^2
- Highest power of 3: 3^1
- LCM (3, 4, 6) = 2^2 x 3^1 = 4 x 3 = 12
Using GCD
For more than two numbers, the GCD method becomes more complex, as you need to apply it iteratively. For instance, to find the LCM of three numbers a, b, and c, you can first find the LCM of a and b, and then find the LCM of the result and c.
LCM (a, b, c) = LCM (LCM (a, b), c)
Example: Find the LCM of 3, 4, and 6.
- Find the LCM of 3 and 4: LCM (3, 4) = 12
- Find the LCM of 12 and 6: LCM (12, 6) = 12
Therefore, the LCM of 3, 4, and 6 is 12.
Common Mistakes
When calculating the LCM, several common mistakes can occur. Being aware of these pitfalls can help prevent errors.
- Confusing LCM with GCD: The LCM and GCD are related but different concepts. The LCM is the smallest common multiple, while the GCD is the largest common divisor. Mixing these up can lead to incorrect results.
- Incorrect Prime Factorization: Ensuring the prime factorization is accurate is crucial. A mistake in the prime factorization will result in an incorrect LCM.
- Missing Prime Factors: When using the prime factorization method, make sure to include all unique prime factors and their highest powers. Omitting a prime factor will lead to an incorrect LCM.
- Arithmetic Errors: Simple arithmetic errors in multiplying the prime factors can also lead to wrong answers. Double-check your calculations to avoid such mistakes.
- Not Finding the Lowest Common Multiple: In the listing multiples method, you might find a common multiple but not necessarily the lowest one. Always ensure that the common multiple you identify is the smallest one.
Advanced Applications of LCM
Beyond basic arithmetic, the LCM has advanced applications in various fields.
- Cryptography: In cryptography, the LCM is used in certain encryption algorithms, especially those based on modular arithmetic.
- Computer Science: In computer science, the LCM can be used in scheduling processes or tasks, optimizing memory allocation, and designing efficient algorithms.
- Engineering: In engineering, the LCM can be used in designing mechanical systems, electrical circuits, and synchronization processes.
- Music Theory: In music theory, the LCM can be used to understand rhythmic patterns and harmonic intervals. For instance, when analyzing polyrhythms, the LCM helps determine when different rhythmic cycles will align.
- Astronomy: In astronomy, the LCM can be used to predict when celestial events will coincide, such as the alignment of planets or the recurrence of comets.
Tips and Tricks
Here are some useful tips and tricks to make calculating the LCM easier:
- Use Prime Factorization for Larger Numbers: For larger numbers, the prime factorization method is generally more efficient than listing multiples.
- Memorize Common Prime Numbers: Knowing the prime numbers up to at least 20 can speed up the prime factorization process.
- Simplify Before Factoring: If possible, simplify the numbers before finding their prime factorizations. For example, if you need to find the LCM of 12 and 18, you can divide both by their common factor 6 to get 2 and 3. Then, find the LCM of 2 and 3 (which is 6) and multiply it by 6 to get the LCM of 12 and 18 (which is 36).
- Use Online Calculators: Many online LCM calculators are available to quickly verify your calculations or find the LCM of multiple numbers.
- Practice Regularly: Consistent practice can improve your speed and accuracy in calculating the LCM. Try working through various examples to build your skills.
- Look for Relationships: Sometimes, you can spot relationships between the numbers that make it easier to find the LCM. For example, if one number is a multiple of the other, then the larger number is the LCM.
Conclusion
The lowest common multiple of 3 and 4 is 12. This fundamental concept is crucial for various mathematical operations and has wide-ranging applications in real-world scenarios. Understanding how to calculate the LCM using different methods, such as listing multiples, prime factorization, and using the GCD, enhances your problem-solving skills and mathematical proficiency. By avoiding common mistakes and practicing regularly, you can master the LCM and apply it effectively in various contexts. Whether you're adding fractions, scheduling tasks, or solving complex mathematical problems, a solid grasp of the LCM is invaluable.
Latest Posts
Latest Posts
-
Ionization Energy Trend Down A Group
Nov 12, 2025
-
What Is A 1 Step Equation
Nov 12, 2025
-
When Does The Law Of Segregation Occur
Nov 12, 2025
-
How Can Using A Credit Card Be Hurtful
Nov 12, 2025
-
What Does Article 7 Of The Constitution Mean
Nov 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lowest Common Multiple Of 3 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.