What Is The Least Common Multiple Of 15 And 12
pinupcasinoyukle
Nov 12, 2025 · 8 min read
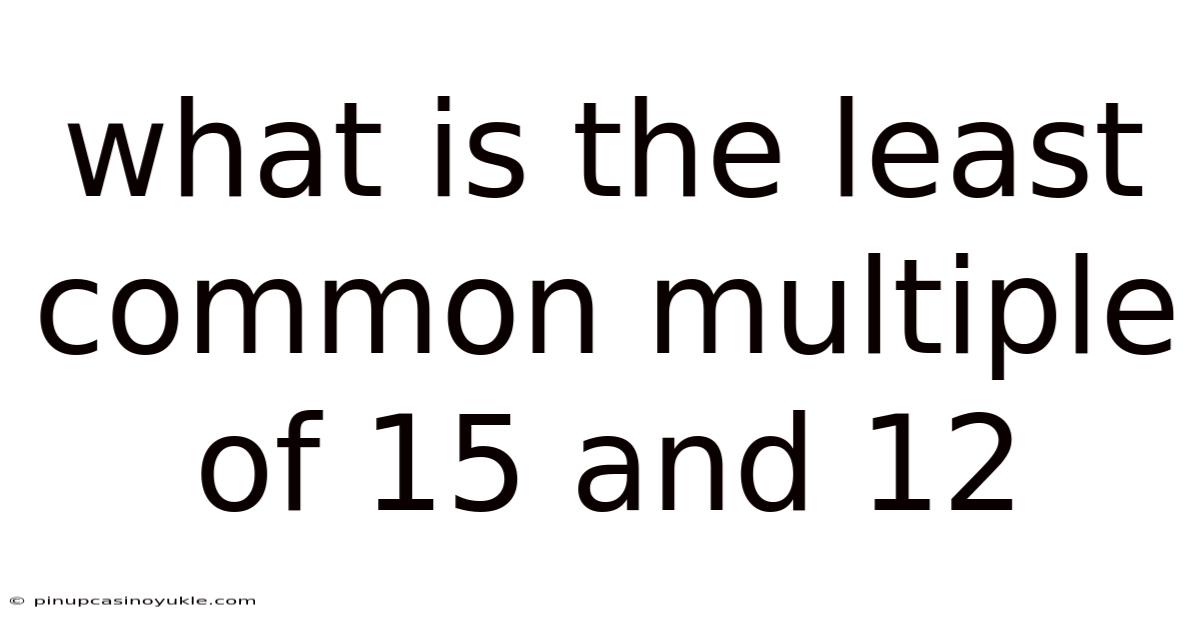
Table of Contents
Determining the least common multiple (LCM) of 15 and 12 is a fundamental exercise in number theory, essential for simplifying fractions, solving algebraic problems, and understanding the relationships between numbers. The LCM is the smallest positive integer that is a multiple of both given numbers. Understanding and calculating the LCM of 15 and 12 involves several methods, each providing unique insights into number theory and arithmetic.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two numbers is the smallest number that is a multiple of both. Multiples are numbers you get when you multiply a number by an integer (e.g., multiples of 3 are 3, 6, 9, 12, and so on). The LCM is crucial in various mathematical operations, particularly when dealing with fractions and algebraic expressions.
Why is LCM Important?
- Fractions: LCM is essential when adding or subtracting fractions with different denominators. It allows you to find a common denominator, making the operation straightforward.
- Algebra: In algebra, LCM is used to simplify expressions, especially when dealing with rational expressions (fractions with polynomials).
- Real-World Applications: LCM appears in scenarios like scheduling events, determining when two processes will align, or understanding cyclical patterns.
Methods to Find the LCM of 15 and 12
There are several methods to find the LCM of 15 and 12, each with its approach and level of complexity. We will explore three primary methods:
- Listing Multiples
- Prime Factorization
- Using the Greatest Common Divisor (GCD)
1. Listing Multiples
One of the simplest ways to find the LCM is by listing the multiples of each number until you find a common multiple.
Steps:
- List Multiples of 15:
- 15, 30, 45, 60, 75, 90, 105, 120, ...
- List Multiples of 12:
- 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, ...
- Identify the Smallest Common Multiple:
- By comparing the lists, the smallest common multiple of 15 and 12 is 60.
Advantages:
- Simple and easy to understand, especially for smaller numbers.
Disadvantages:
- Can be time-consuming and impractical for larger numbers, as you may need to list many multiples.
2. Prime Factorization
Prime factorization involves expressing each number as a product of its prime factors. This method is particularly efficient and provides a deeper understanding of the numbers' composition.
Steps:
- Find the Prime Factorization of 15:
- 15 = 3 x 5
- Find the Prime Factorization of 12:
- 12 = 2 x 2 x 3 = 2<sup>2</sup> x 3
- Identify the Highest Power of Each Prime Factor:
- For 2: The highest power is 2<sup>2</sup> (from 12)
- For 3: The highest power is 3<sup>1</sup> (present in both 15 and 12)
- For 5: The highest power is 5<sup>1</sup> (from 15)
- Multiply the Highest Powers of All Prime Factors:
- LCM(15, 12) = 2<sup>2</sup> x 3<sup>1</sup> x 5<sup>1</sup> = 4 x 3 x 5 = 60
Advantages:
- Efficient and reliable, especially for larger numbers.
- Provides insight into the structure of the numbers.
Disadvantages:
- Requires knowledge of prime factorization.
3. Using the Greatest Common Divisor (GCD)
The greatest common divisor (GCD) of two numbers is the largest positive integer that divides both numbers without leaving a remainder. The GCD method involves finding the GCD first and then using it to calculate the LCM.
Steps:
- Find the Greatest Common Divisor (GCD) of 15 and 12:
- Factors of 15: 1, 3, 5, 15
- Factors of 12: 1, 2, 3, 4, 6, 12
- The GCD of 15 and 12 is 3.
- Use the Formula:
- LCM(a, b) = (|a x b|) / GCD(a, b)
- LCM(15, 12) = (|15 x 12|) / 3 = 180 / 3 = 60
Advantages:
- Useful when the GCD is easily found.
- Provides a clear relationship between GCD and LCM.
Disadvantages:
- Requires an extra step to find the GCD first.
Step-by-Step Examples
To solidify understanding, let's walk through each method step-by-step.
Example 1: Listing Multiples
- List Multiples of 15:
- 15 x 1 = 15
- 15 x 2 = 30
- 15 x 3 = 45
- 15 x 4 = 60
- 15 x 5 = 75
- List Multiples of 12:
- 12 x 1 = 12
- 12 x 2 = 24
- 12 x 3 = 36
- 12 x 4 = 48
- 12 x 5 = 60
- 12 x 6 = 72
- Identify the Smallest Common Multiple:
- The smallest multiple that appears in both lists is 60.
Example 2: Prime Factorization
- Prime Factorization of 15:
- 15 = 3 x 5
- Prime Factorization of 12:
- 12 = 2 x 2 x 3 = 2<sup>2</sup> x 3
- Identify Highest Powers:
- 2<sup>2</sup> from 12
- 3<sup>1</sup> from both 15 and 12
- 5<sup>1</sup> from 15
- Multiply Highest Powers:
- LCM = 2<sup>2</sup> x 3<sup>1</sup> x 5<sup>1</sup> = 4 x 3 x 5 = 60
Example 3: Using the GCD
- Find GCD of 15 and 12:
- Factors of 15: 1, 3, 5, 15
- Factors of 12: 1, 2, 3, 4, 6, 12
- GCD = 3
- Apply the Formula:
- LCM(15, 12) = (|15 x 12|) / GCD(15, 12)
- LCM(15, 12) = (180) / 3 = 60
Practical Applications of LCM
Understanding and calculating the LCM has practical applications in various fields and daily scenarios.
1. Scheduling Problems
Consider two events that occur at regular intervals. One event happens every 15 days, and another happens every 12 days. When will both events occur on the same day again?
- Solution:
- Find the LCM of 15 and 12.
- LCM(15, 12) = 60
- Both events will occur on the same day again in 60 days.
2. Fraction Simplification
When adding or subtracting fractions with different denominators, the LCM helps find a common denominator.
- Example:
- Add 1/15 and 1/12
- LCM(15, 12) = 60
- Convert fractions to have a common denominator of 60:
- 1/15 = 4/60
- 1/12 = 5/60
- Add the fractions: 4/60 + 5/60 = 9/60
- Simplify the fraction: 9/60 = 3/20
3. Manufacturing and Engineering
In manufacturing, LCM can be used to synchronize machines or processes that operate at different cycles.
- Example:
- Machine A completes a cycle in 15 seconds, and Machine B completes a cycle in 12 seconds. How often will both machines complete a cycle simultaneously?
- Solution:
- Find the LCM of 15 and 12.
- LCM(15, 12) = 60
- Both machines will complete a cycle simultaneously every 60 seconds.
Advanced Concepts Related to LCM
Understanding the LCM also opens the door to more advanced concepts in number theory.
1. Relationship Between LCM and GCD
The LCM and GCD are related by the formula:
- LCM(a, b) x GCD(a, b) = |a x b|
- This relationship is fundamental in number theory and provides a way to verify calculations.
2. LCM of More Than Two Numbers
The concept of LCM can be extended to more than two numbers. To find the LCM of multiple numbers, you can find the LCM of the first two numbers, then find the LCM of that result and the next number, and so on.
- Example:
- Find the LCM of 15, 12, and 10.
- LCM(15, 12) = 60
- LCM(60, 10) = 60 (since 60 is a multiple of 10)
- LCM(15, 12, 10) = 60
- Find the LCM of 15, 12, and 10.
3. Applications in Cryptography
While not directly used, the principles behind LCM and GCD are essential in understanding modular arithmetic, which is a foundation of many cryptographic algorithms.
Common Mistakes to Avoid
When calculating the LCM, several common mistakes can lead to incorrect results.
1. Confusing LCM with GCD
- Mistake: Confusing the definitions of LCM and GCD.
- Correction: Remember that LCM is the smallest multiple, while GCD is the largest divisor.
2. Incorrect Prime Factorization
- Mistake: Incorrectly factoring numbers into primes.
- Correction: Double-check your prime factorization to ensure accuracy.
3. Missing Prime Factors
- Mistake: Forgetting to include all prime factors when using the prime factorization method.
- Correction: Ensure you consider all prime factors from each number when computing the LCM.
4. Arithmetic Errors
- Mistake: Making simple arithmetic errors in calculations.
- Correction: Use a calculator or double-check your calculations to avoid mistakes.
Practice Questions
To reinforce your understanding, try solving these practice questions:
- Find the LCM of 18 and 24.
- Find the LCM of 16 and 20.
- Find the LCM of 8, 12, and 15.
Solutions:
- LCM of 18 and 24:
- Prime factorization: 18 = 2 x 3<sup>2</sup>, 24 = 2<sup>3</sup> x 3
- LCM = 2<sup>3</sup> x 3<sup>2</sup> = 8 x 9 = 72
- LCM of 16 and 20:
- Prime factorization: 16 = 2<sup>4</sup>, 20 = 2<sup>2</sup> x 5
- LCM = 2<sup>4</sup> x 5 = 16 x 5 = 80
- LCM of 8, 12, and 15:
- Prime factorization: 8 = 2<sup>3</sup>, 12 = 2<sup>2</sup> x 3, 15 = 3 x 5
- LCM = 2<sup>3</sup> x 3 x 5 = 8 x 3 x 5 = 120
Conclusion
The least common multiple (LCM) of 15 and 12 is 60. Understanding how to calculate the LCM is a valuable skill in mathematics with applications ranging from simplifying fractions to solving real-world problems. By mastering the methods of listing multiples, prime factorization, and using the GCD, you can confidently tackle LCM problems and appreciate their significance in various contexts.
Latest Posts
Latest Posts
-
Organisms That Can Produce Their Own Food Through Photosynthesis
Nov 12, 2025
-
What Is 1 6 As A Fraction
Nov 12, 2025
-
How Many Pounds In 18 Oz
Nov 12, 2025
-
Postulates Of The Kinetic Molecular Theory
Nov 12, 2025
-
What Is The Difference Between Phagocytosis And Pinocytosis
Nov 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 15 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.