What Is The Gcf Of 8 And 20
pinupcasinoyukle
Nov 27, 2025 · 8 min read
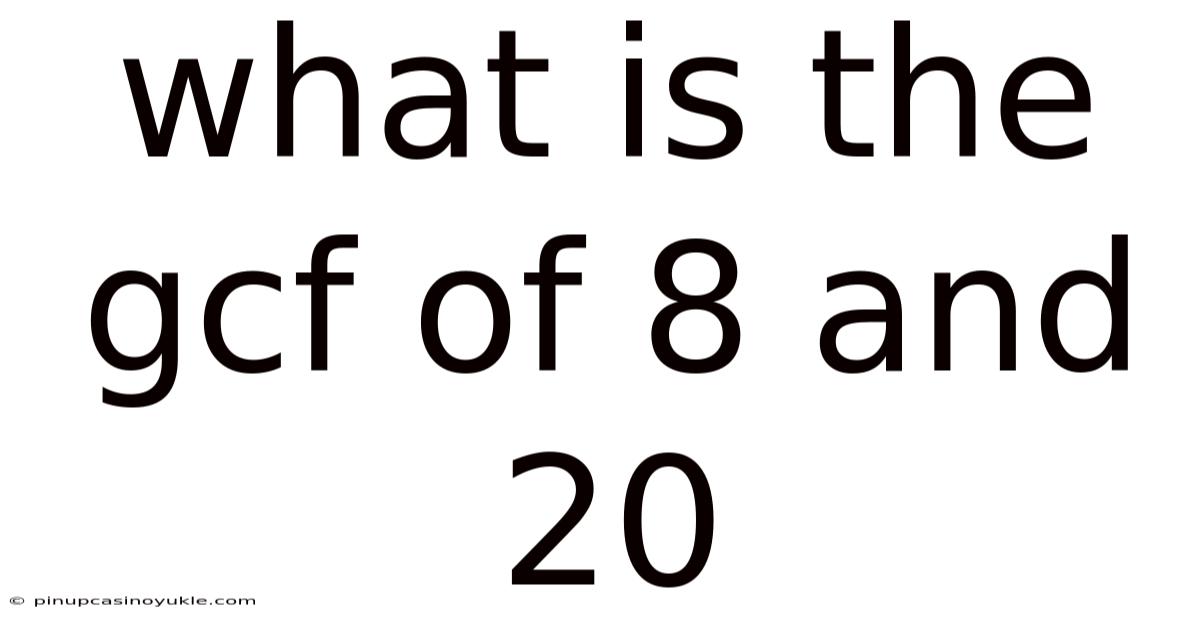
Table of Contents
Unlocking the Greatest Common Factor: Finding the GCF of 8 and 20
The greatest common factor (GCF), also known as the highest common factor (HCF), is a fundamental concept in mathematics, especially in number theory. Understanding how to find the GCF is essential for simplifying fractions, solving algebraic problems, and grasping more complex mathematical ideas. In this comprehensive guide, we will explore the GCF of 8 and 20 in detail, examining various methods to calculate it and providing clear, step-by-step explanations for each approach.
Understanding the Greatest Common Factor (GCF)
Before diving into specific methods, it's crucial to understand what the GCF represents. The GCF of two or more numbers is the largest positive integer that divides each of the numbers without leaving a remainder. In simpler terms, it's the biggest number that can evenly divide both numbers.
For instance, if we want to find the GCF of 8 and 20, we are looking for the largest number that can divide both 8 and 20 perfectly. This concept is useful in many real-world scenarios, such as dividing items into equal groups or simplifying ratios.
Why is Finding the GCF Important?
Finding the GCF is not just a mathematical exercise; it has practical applications:
- Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, if you have a fraction like 8/20, finding the GCF of 8 and 20 allows you to divide both the numerator and the denominator by the GCF, resulting in a simplified fraction.
- Solving Algebraic Equations: The GCF can be used to factor expressions in algebra, making it easier to solve equations.
- Real-World Applications: In everyday life, the GCF can help in dividing items into equal groups, determining the largest size of a square that can tile a rectangular area, and more.
Now, let’s explore the different methods to find the GCF of 8 and 20.
Method 1: Listing Factors
One of the simplest ways to find the GCF of two numbers is by listing their factors. A factor of a number is an integer that divides the number without leaving a remainder.
Step 1: List the factors of each number.
- Factors of 8: 1, 2, 4, 8
- Factors of 20: 1, 2, 4, 5, 10, 20
Step 2: Identify the common factors.
Looking at the lists above, the common factors of 8 and 20 are: 1, 2, and 4.
Step 3: Determine the greatest common factor.
Among the common factors (1, 2, and 4), the greatest is 4.
Therefore, the GCF of 8 and 20 is 4.
This method is straightforward and easy to understand, making it a great starting point for grasping the concept of GCF.
Method 2: Prime Factorization
Prime factorization involves expressing each number as a product of its prime factors. A prime number is a number greater than 1 that has only two factors: 1 and itself (e.g., 2, 3, 5, 7, 11).
Step 1: Find the prime factorization of each number.
- Prime factorization of 8: (2 \times 2 \times 2 = 2^3)
- Prime factorization of 20: (2 \times 2 \times 5 = 2^2 \times 5)
Step 2: Identify the common prime factors.
In this case, both 8 and 20 share the prime factor 2.
Step 3: Determine the lowest power of each common prime factor.
- The lowest power of 2 in the prime factorizations is (2^2).
Step 4: Multiply the lowest powers of the common prime factors.
- (2^2 = 4)
Therefore, the GCF of 8 and 20 is 4.
Prime factorization is particularly useful when dealing with larger numbers because it breaks down the numbers into their fundamental components, making it easier to identify common factors.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers. It involves repeatedly applying the division algorithm until the remainder is zero. The last non-zero remainder is the GCF.
Step 1: Divide the larger number by the smaller number and find the remainder.
- Divide 20 by 8: (20 = 8 \times 2 + 4)
- The remainder is 4.
Step 2: If the remainder is zero, the smaller number is the GCF. If not, replace the larger number with the smaller number and the smaller number with the remainder, then repeat the process.
- Now, divide 8 by the remainder 4: (8 = 4 \times 2 + 0)
- The remainder is 0.
Step 3: The last non-zero remainder is the GCF.
- Since the remainder is now 0, the previous remainder (4) is the GCF.
Therefore, the GCF of 8 and 20 is 4.
The Euclidean algorithm is particularly useful when dealing with very large numbers, as it reduces the problem to a series of simpler divisions.
Comparative Analysis of the Methods
Each of the methods discussed above has its advantages and disadvantages:
- Listing Factors:
- Advantages: Simple and easy to understand, especially for small numbers.
- Disadvantages: Can be time-consuming and impractical for large numbers with many factors.
- Prime Factorization:
- Advantages: Works well for a range of numbers, breaks down numbers into fundamental components.
- Disadvantages: Can be challenging to find the prime factors of very large numbers.
- Euclidean Algorithm:
- Advantages: Efficient, especially for large numbers; requires only division.
- Disadvantages: Requires understanding of the division algorithm.
For finding the GCF of 8 and 20, all three methods are relatively straightforward. However, the Euclidean algorithm is generally considered the most efficient, especially as the numbers get larger.
Real-World Examples of GCF Application
To illustrate the practical application of finding the GCF, let's consider a few real-world examples:
- Dividing Items into Equal Groups:
- Suppose you have 8 apples and 20 oranges and you want to divide them into equal groups with no leftovers. To find the largest number of groups you can make, you need to find the GCF of 8 and 20, which is 4. This means you can make 4 groups, each containing 2 apples and 5 oranges.
- Simplifying Ratios:
- Consider a recipe that calls for 8 tablespoons of sugar and 20 tablespoons of flour. To simplify the ratio, you find the GCF of 8 and 20, which is 4. Dividing both quantities by 4, you get a simplified ratio of 2:5. This means for every 2 tablespoons of sugar, you need 5 tablespoons of flour.
- Tiling a Rectangular Area:
- You have a rectangular area that is 8 feet by 20 feet, and you want to tile it with the largest possible square tiles. To find the side length of the largest square tile, you need to find the GCF of 8 and 20, which is 4. This means you can use square tiles with sides of 4 feet each.
Common Mistakes to Avoid
When finding the GCF, it’s important to avoid common mistakes:
- Confusing GCF with LCM (Least Common Multiple):
- The GCF is the largest number that divides both numbers, while the LCM is the smallest number that both numbers divide into. Confusing these two can lead to incorrect answers.
- Incorrectly Listing Factors:
- Ensure you list all the factors of each number. Missing a factor can lead to an incorrect GCF.
- Making Errors in Prime Factorization:
- Double-check your prime factorization to ensure accuracy.
- Misapplying the Euclidean Algorithm:
- Follow the steps of the Euclidean algorithm carefully to avoid mistakes. Ensure you divide correctly and use the remainders appropriately.
Advanced Tips and Tricks for Finding GCF
Here are some advanced tips and tricks to help you become more proficient at finding the GCF:
- Use Divisibility Rules:
- Understanding divisibility rules (e.g., a number is divisible by 2 if it is even, by 3 if the sum of its digits is divisible by 3, by 5 if it ends in 0 or 5) can help you quickly identify factors.
- Recognize Common Factors:
- Practice recognizing common factors quickly. For instance, if both numbers are even, you know that 2 is a common factor.
- Use Technology:
- Utilize calculators or online tools to find the prime factorization or GCF of numbers, especially when dealing with large numbers.
- Practice Regularly:
- The more you practice, the faster and more accurate you will become at finding the GCF.
GCF in More Complex Scenarios
The concept of GCF extends to more complex scenarios, such as finding the GCF of multiple numbers or algebraic expressions.
GCF of Multiple Numbers
To find the GCF of more than two numbers, you can follow these steps:
- Find the GCF of the first two numbers.
- Find the GCF of the result from step 1 and the third number.
- Continue this process until you have included all the numbers.
For example, to find the GCF of 8, 20, and 24:
- GCF(8, 20) = 4
- GCF(4, 24) = 4
Therefore, the GCF of 8, 20, and 24 is 4.
GCF of Algebraic Expressions
The GCF can also be applied to algebraic expressions. To find the GCF of algebraic expressions, identify the common variables and their lowest powers, as well as the GCF of the coefficients.
For example, to find the GCF of (8x^2y) and (20xy^3):
- Find the GCF of the coefficients: GCF(8, 20) = 4
- Identify the common variables and their lowest powers:
- Common variables: (x) and (y)
- Lowest power of (x): (x^1 = x)
- Lowest power of (y): (y^1 = y)
Therefore, the GCF of (8x^2y) and (20xy^3) is (4xy).
Conclusion
Finding the greatest common factor (GCF) is a fundamental skill in mathematics with numerous practical applications. Whether you choose to list factors, use prime factorization, or apply the Euclidean algorithm, understanding the underlying concepts and practicing regularly will enhance your ability to find the GCF efficiently.
In the case of 8 and 20, the GCF is 4, which means 4 is the largest number that can divide both 8 and 20 without leaving a remainder. By mastering these techniques, you’ll be well-equipped to tackle more complex mathematical problems and apply these skills in real-world situations. Remember to avoid common mistakes, utilize advanced tips, and continue practicing to solidify your understanding.
Latest Posts
Latest Posts
-
Are Dipole Dipole Forces Intermolecular Or Intramolecular
Nov 27, 2025
-
Derivatives Of Exponential And Log Functions
Nov 27, 2025
-
Step By Step Solving Multi Step Equations
Nov 27, 2025
-
Do Non Polar Molecules Dissolve In Water
Nov 27, 2025
-
What Is A Position Vs Time Graph
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 8 And 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.