What Is Lcm Of 5 And 6
pinupcasinoyukle
Nov 12, 2025 · 10 min read
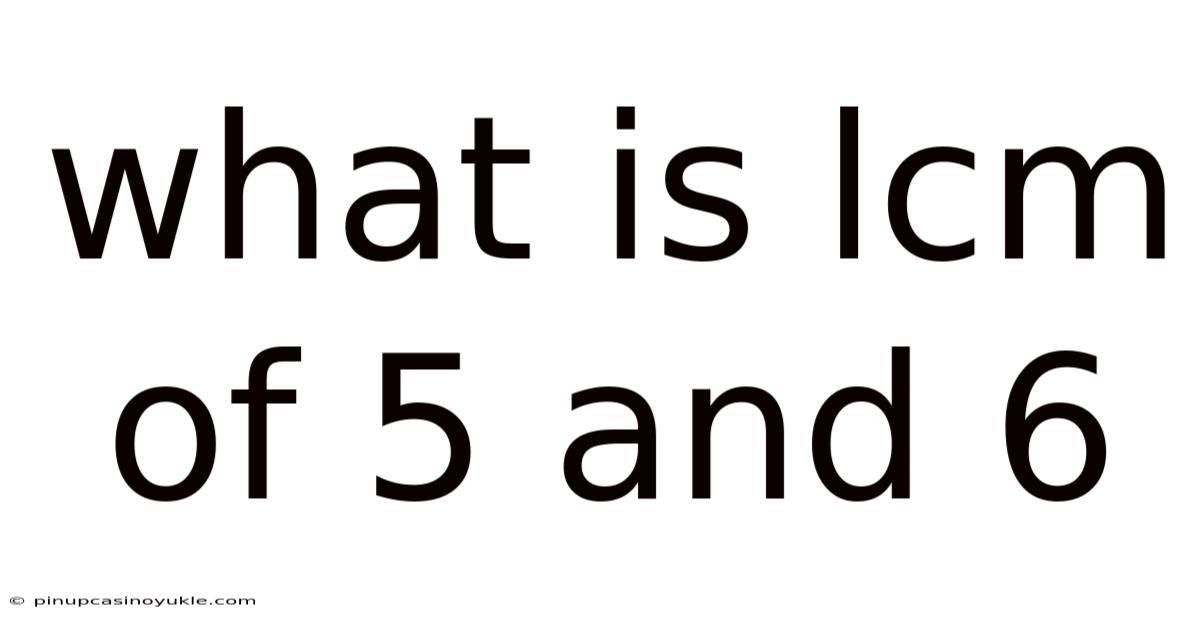
Table of Contents
Finding the Least Common Multiple (LCM) of two or more numbers is a fundamental concept in arithmetic and number theory, essential for various mathematical operations such as simplifying fractions and solving algebraic equations. When you're trying to determine the LCM of 5 and 6, you're essentially looking for the smallest positive integer that is divisible by both numbers without leaving a remainder.
Understanding the Least Common Multiple (LCM)
The Least Common Multiple (LCM), also known as the Lowest Common Multiple, is the smallest positive integer that is perfectly divisible by two or more numbers. This concept is crucial in simplifying fractions, solving problems involving time and distance, and understanding the relationships between numbers. Unlike the Greatest Common Divisor (GCD), which seeks the largest factor shared by two numbers, the LCM focuses on finding a multiple that is common to both.
Why is LCM Important?
Understanding the LCM is critical for several reasons:
- Simplifying Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators allows you to rewrite the fractions with a common denominator, making the operation straightforward.
- Problem Solving: In various real-world scenarios, such as scheduling events that occur at different intervals, the LCM helps determine when events will coincide.
- Mathematical Foundations: The LCM is a building block for more advanced mathematical concepts and is used in fields like algebra, number theory, and cryptography.
Methods to Find the LCM of 5 and 6
There are several methods to calculate the LCM of 5 and 6, each with its own advantages and level of complexity. Here are three common methods:
- Listing Multiples
- Prime Factorization
- Using the GCD (Greatest Common Divisor)
1. Listing Multiples
This method involves listing the multiples of each number until you find a common multiple. It's straightforward and easy to understand, making it suitable for smaller numbers.
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, ...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, ...
From the lists above, we can see that the smallest multiple that appears in both lists is 30. Therefore, the LCM of 5 and 6 is 30. This method is practical when dealing with small numbers but can become cumbersome for larger numbers, as it requires generating long lists of multiples.
2. Prime Factorization
The prime factorization method breaks down each number into its prime factors and then combines these factors to find the LCM. This method is more efficient for larger numbers.
- Prime factorization of 5: 5 (since 5 is a prime number)
- Prime factorization of 6: 2 x 3
To find the LCM, take the highest power of each prime factor that appears in either factorization and multiply them together:
- LCM (5, 6) = 2 x 3 x 5 = 30
This method ensures that the LCM is divisible by both numbers because it includes all the necessary prime factors. It's a reliable method that works well for any set of numbers, regardless of size.
3. Using the GCD (Greatest Common Divisor)
The GCD method utilizes the relationship between the LCM and the GCD of two numbers. The formula is:
- LCM (a, b) = (a x b) / GCD (a, b)
First, find the GCD of 5 and 6. The factors of 5 are 1 and 5, and the factors of 6 are 1, 2, 3, and 6. The only common factor is 1, so:
- GCD (5, 6) = 1
Now, use the formula to find the LCM:
- LCM (5, 6) = (5 x 6) / 1 = 30 / 1 = 30
This method is efficient when you already know the GCD or can easily find it. It's particularly useful when dealing with larger numbers where finding prime factors might be more challenging.
Step-by-Step Calculation of LCM of 5 and 6 Using Prime Factorization
Prime factorization is one of the most reliable methods for finding the LCM, especially useful for larger numbers. Here’s a detailed, step-by-step guide to calculating the LCM of 5 and 6 using prime factorization:
- Identify the Numbers:
- We need to find the LCM of 5 and 6.
- Prime Factorization of Each Number:
- Prime Factorization of 5:
- Since 5 is a prime number, its only factors are 1 and itself. Therefore, the prime factorization of 5 is simply 5.
- Prime Factorization of 6:
- To find the prime factors of 6, we can divide it by the smallest prime number, which is 2:
- 6 ÷ 2 = 3
- 3 is also a prime number, so we stop here. The prime factorization of 6 is 2 x 3.
- To find the prime factors of 6, we can divide it by the smallest prime number, which is 2:
- Prime Factorization of 5:
- List the Prime Factors:
- Prime factors of 5: 5
- Prime factors of 6: 2, 3
- Identify the Highest Power of Each Prime Factor:
- For each prime factor, identify the highest power that appears in either factorization:
- 2 appears in the factorization of 6 as 2^1.
- 3 appears in the factorization of 6 as 3^1.
- 5 appears in the factorization of 5 as 5^1.
- For each prime factor, identify the highest power that appears in either factorization:
- Multiply the Highest Powers of All Prime Factors:
- Multiply all the identified highest powers of prime factors together:
- LCM (5, 6) = 2^1 x 3^1 x 5^1 = 2 x 3 x 5
- Multiply all the identified highest powers of prime factors together:
- Calculate the Result:
- Multiply the numbers together to get the LCM:
- 2 x 3 x 5 = 30
- Multiply the numbers together to get the LCM:
Therefore, the LCM of 5 and 6 is 30.
Practical Examples and Applications
Understanding the LCM is not just a theoretical exercise; it has numerous practical applications in everyday life. Here are a few examples to illustrate how the LCM can be used:
- Scheduling:
- Imagine you have two tasks: one that needs to be done every 5 days and another that needs to be done every 6 days. If you start both tasks today, when will you do both tasks on the same day again?
- To solve this, you need to find the LCM of 5 and 6, which is 30. Therefore, you will do both tasks together again in 30 days.
- Cooking and Baking:
- In cooking, you might need to adjust recipes that serve different numbers of people. If one recipe serves 5 people and another serves 6, and you want to combine them to serve a larger group, understanding the LCM can help you adjust the quantities accurately.
- Travel Planning:
- Suppose you are coordinating a trip with friends. One friend can only travel every 5 weeks, and another can only travel every 6 weeks. When will both friends be available to travel together?
- Again, the LCM of 5 and 6 is 30. This means both friends will be available to travel together every 30 weeks.
- Simplifying Fractions:
- Adding fractions such as 1/5 and 1/6 requires finding a common denominator. The LCM of 5 and 6 is 30, so you can rewrite the fractions as 6/30 and 5/30, making the addition straightforward:
- 1/5 + 1/6 = 6/30 + 5/30 = 11/30
- Adding fractions such as 1/5 and 1/6 requires finding a common denominator. The LCM of 5 and 6 is 30, so you can rewrite the fractions as 6/30 and 5/30, making the addition straightforward:
Common Mistakes to Avoid
When calculating the LCM, it's easy to make mistakes, especially if you're not careful. Here are some common pitfalls to avoid:
- Confusing LCM with GCD:
- The LCM and GCD are related but different concepts. The LCM is the smallest common multiple, while the GCD is the largest common divisor. Make sure you understand which one you need to find.
- Incorrect Prime Factorization:
- Ensure that you correctly identify the prime factors of each number. A mistake in the prime factorization will lead to an incorrect LCM.
- Missing Prime Factors:
- When using the prime factorization method, make sure you include all the prime factors from both numbers, using the highest power of each.
- Arithmetic Errors:
- Simple arithmetic errors can lead to incorrect results. Double-check your calculations, especially when multiplying the prime factors together.
- Stopping Too Early:
- When listing multiples, make sure you list enough multiples to find a common one. Sometimes the common multiple is not immediately apparent.
Advanced Concepts Related to LCM
While understanding the basic concept of LCM is essential, there are more advanced topics related to it that can deepen your understanding:
- LCM of Three or More Numbers:
- The concept of LCM can be extended to three or more numbers. To find the LCM of multiple numbers, you can use the prime factorization method or find the LCM of two numbers at a time.
- Relationship Between LCM and GCD:
- The relationship between LCM and GCD is fundamental in number theory. For any two positive integers a and b:
- LCM (a, b) x GCD (a, b) = a x b
- This relationship can be used to find the LCM if you know the GCD, or vice versa.
- The relationship between LCM and GCD is fundamental in number theory. For any two positive integers a and b:
- Applications in Abstract Algebra:
- In abstract algebra, the concept of LCM is generalized to algebraic structures like rings and modules. Understanding LCM in these contexts requires a deeper knowledge of algebraic concepts.
- LCM in Cryptography:
- While not a direct application, the principles of number theory, including LCM and GCD, are used in cryptography to design secure encryption algorithms.
LCM in Real Life
The Least Common Multiple (LCM) isn't just a concept confined to textbooks; it's a practical tool that helps solve problems in various real-life scenarios. Here are a few examples that highlight its relevance:
- Event Scheduling: Imagine you're organizing a community event that involves different groups. One group meets every 4 days for rehearsals, another meets every 6 days for planning, and a third meets every 8 days for fundraising. To coordinate a day when all three groups can come together, you need to find the LCM of 4, 6, and 8. The LCM is 24, meaning that every 24 days, all three groups will have their meetings on the same day.
- Manufacturing and Inventory: A factory produces two types of products. Product A requires a quality check every 10 days, while Product B requires a check every 15 days. To optimize the scheduling of quality control, the manager needs to know when both products will require checking on the same day. The LCM of 10 and 15 is 30, so every 30 days, both products will be checked together, streamlining the quality control process.
- Music and Rhythms: In music, the LCM can be used to understand repeating patterns in different rhythms. For instance, if one musical phrase repeats every 12 beats and another repeats every 16 beats, the LCM of 12 and 16 (which is 48) tells you that every 48 beats, both phrases will align. This knowledge can help composers create complex and harmonious pieces.
- Gardening: A gardener plants two types of flowers. One type needs watering every 3 days, while the other needs fertilizing every 7 days. To efficiently plan the gardening tasks, the gardener needs to know when both tasks will coincide. The LCM of 3 and 7 is 21, so every 21 days, the gardener will need to water the first type of flower and fertilize the second type on the same day.
Conclusion
Finding the LCM of numbers like 5 and 6 is a foundational skill in mathematics with far-reaching implications. Whether you choose to list multiples, use prime factorization, or apply the GCD formula, understanding the underlying principles will empower you to solve a wide range of problems. From simplifying fractions to coordinating complex schedules, the LCM is a valuable tool in both academic and real-world contexts. By mastering these methods and avoiding common mistakes, you can confidently tackle LCM-related challenges and appreciate the elegance and utility of this mathematical concept.
Latest Posts
Latest Posts
-
What Is The Difference Between Cytoplasm And Cytosol
Nov 12, 2025
-
Major And Minor Grooves In Dna
Nov 12, 2025
-
Solution That Binds To Proteins To Make Them Uniformly Negative
Nov 12, 2025
-
The Tendency Of An Object To Resist Change
Nov 12, 2025
-
Sensory Stimuli Cause Activation Of An Endocrine Gland
Nov 12, 2025
Related Post
Thank you for visiting our website which covers about What Is Lcm Of 5 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.