What Is A Positive Divided By A Negative
pinupcasinoyukle
Nov 04, 2025 · 7 min read
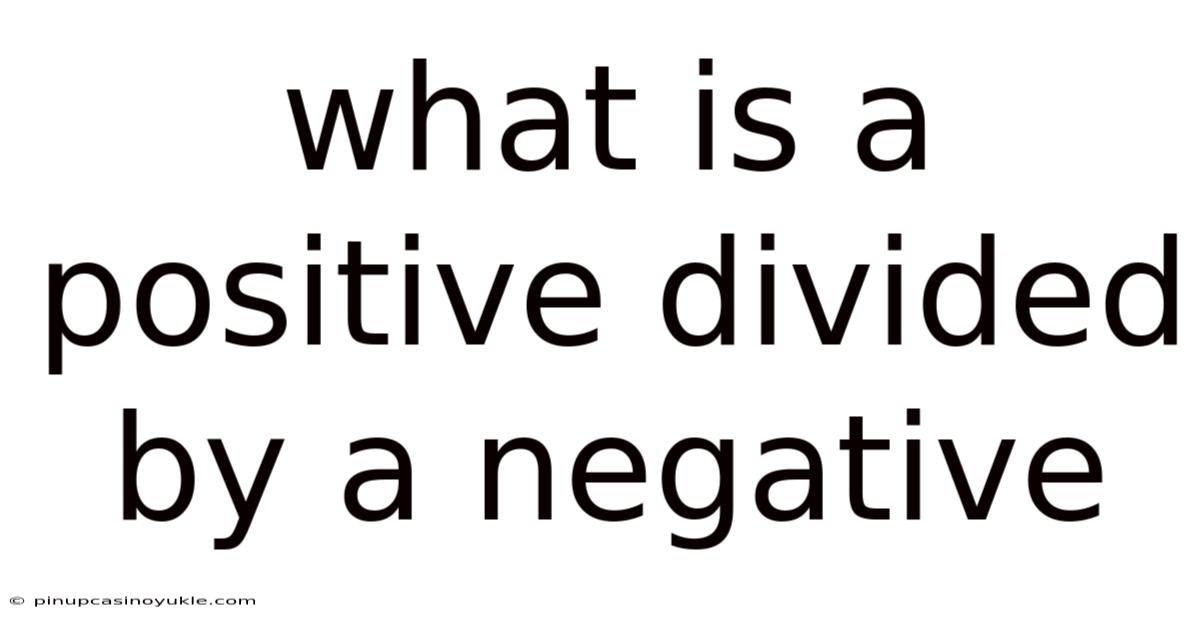
Table of Contents
Dividing a positive number by a negative number always results in a negative quotient. This fundamental principle of arithmetic stems from the rules governing the signs of numbers in mathematical operations, ensuring consistency and predictability in calculations.
Understanding Positive and Negative Numbers
Before diving into the specifics of division, it's crucial to have a firm grasp of what positive and negative numbers represent. Positive numbers are greater than zero and are typically used to represent quantities or values above a certain reference point. They are often denoted with a plus sign (+), although this sign is usually omitted. For example, +5 is the same as 5, and it represents a value five units greater than zero.
Negative numbers, on the other hand, are less than zero. They represent quantities or values below a reference point. These numbers are always denoted with a minus sign (-). For example, -3 represents a value three units less than zero.
These numbers are fundamental to understanding concepts like debt (negative) versus assets (positive), temperature above (positive) or below (negative) freezing, and direction (positive for forward, negative for backward).
The Basics of Division
Division is one of the four basic arithmetic operations, the others being addition, subtraction, and multiplication. It's essentially the inverse operation of multiplication. In simple terms, division involves splitting a quantity into equal parts.
A division problem has three main components:
- Dividend: The number being divided (the quantity to be split).
- Divisor: The number by which the dividend is being divided (the number of equal parts).
- Quotient: The result of the division (the size of each equal part).
The division can be represented as:
Dividend / Divisor = Quotient
For example, in the division problem 12 / 3 = 4, 12 is the dividend, 3 is the divisor, and 4 is the quotient.
Rules of Signs in Division
When performing division with signed numbers (positive and negative numbers), the sign of the quotient depends on the signs of the dividend and the divisor. There are specific rules that govern these operations:
- Positive / Positive = Positive: When a positive number is divided by a positive number, the result is always positive. This is the most straightforward case, as it aligns with our intuitive understanding of division.
- Negative / Negative = Positive: When a negative number is divided by a negative number, the result is also positive. This might seem counterintuitive at first, but it's a crucial rule to remember.
- Positive / Negative = Negative: When a positive number is divided by a negative number, the result is negative. This is the rule we're focusing on in this article.
- Negative / Positive = Negative: When a negative number is divided by a positive number, the result is also negative.
These rules can be summarized in a simple table:
| Dividend Sign | Divisor Sign | Quotient Sign |
|---|---|---|
| Positive | Positive | Positive |
| Negative | Negative | Positive |
| Positive | Negative | Negative |
| Negative | Positive | Negative |
Why is a Positive Divided by a Negative Always Negative?
The fact that a positive divided by a negative always yields a negative quotient can be understood through several different perspectives:
1. The Inverse Relationship with Multiplication
As mentioned earlier, division is the inverse operation of multiplication. This means that if a / b = c, then b * c = a. We can use this relationship to understand the rules of signs in division.
Let's consider the case of a positive number divided by a negative number: +a / -b = c. According to the inverse relationship, this means that -b * c = +a.
To satisfy this equation, c must be a negative number. If c were positive, then -b * +c would result in a negative number, which contradicts the fact that -b * c = +a. Therefore, c must be negative, meaning that a positive number divided by a negative number always results in a negative quotient.
2. Using Number Line Visualization
The number line provides a visual way to understand the division of signed numbers. Consider dividing a positive number, say +6, by a negative number, say -2. This can be interpreted as asking: "How many steps of -2 do we need to take from 0 to reach +6?".
To visualize this, start at 0 on the number line. Since we're dividing by a negative number, we're moving in the negative direction. To reach +6, we need to move in the opposite direction (the positive direction).
- One step of -2 takes us to -2.
- Another step of -2 takes us to -4.
- A third step of -2 takes us to -6.
Now, we're at -6, which is the negative of +6. To reach +6, we need to reverse the direction. Since we took three steps of -2 to reach -6, it means we need to take -3 steps of -2 to reach +6. Therefore, +6 / -2 = -3.
This visualization demonstrates that dividing a positive number by a negative number involves moving in the opposite direction on the number line, resulting in a negative quotient.
3. Real-World Examples
Real-world examples can also help illustrate why a positive divided by a negative results in a negative.
- Sharing Debt: Imagine you have a debt of $100 (represented as +100 because it's an amount you owe). You want to split this debt equally among 5 people (represented as -5 because they are receiving the debt). What is each person's share of the debt? You are essentially calculating +100 / -5. Each person will be responsible for $20 of the debt, which is represented as -20 (because it's a debt they owe).
- Rate of Descent: Suppose an airplane descends 2000 feet (positive) over a period of 10 minutes (negative, representing time elapsed backwards from a future point). What is the average rate of descent per minute? The calculation is +2000 / -10. The average rate of descent is -200 feet per minute (negative because it's a descent).
These examples highlight that dividing a positive quantity by a negative quantity often represents distributing something away from a starting point or experiencing a decrease, resulting in a negative value.
Examples of Positive Divided by Negative
Let's look at some specific examples:
- 10 / -2 = -5
- 25 / -5 = -5
- 100 / -4 = -25
- 1 / -1 = -1
- 15 / -3 = -5
- 42 / -6 = -7
- 8 / -2 = -4
- 21 / -7 = -3
- 50 / -10 = -5
- 12 / -4 = -3
In each of these examples, a positive number is divided by a negative number, and the resulting quotient is always negative.
Common Mistakes to Avoid
When working with division involving signed numbers, there are some common mistakes to watch out for:
- Forgetting the Sign: One of the most frequent errors is forgetting to apply the correct sign to the quotient. Always remember to determine the sign of the answer before performing the actual division.
- Confusing Division with Multiplication: Although division and multiplication are related, they are distinct operations. It's essential to apply the correct rules for each operation. For example, a negative times a negative is positive, but a positive divided by a negative is negative.
- Misinterpreting Real-World Context: In word problems, carefully consider the context to determine the correct signs for the numbers involved. A debt is negative, while an asset is positive. Descent is negative, while ascent is positive.
Practice Problems
To solidify your understanding, try solving the following practice problems:
- 36 / -9 = ?
- 144 / -12 = ?
- 20 / -4 = ?
- 1000 / -100 = ?
- 72 / -8 = ?
Answers:
- -4
- -12
- -5
- -10
- -9
Advanced Concepts
The principle of positive divided by negative extending to more advanced mathematical concepts, including:
- Algebra: In algebraic equations, the rules of signs are crucial for solving for unknown variables. For example, if you have the equation -2x = 10, you would divide both sides by -2 to solve for x, resulting in x = -5.
- Calculus: In calculus, the concept of derivatives involves finding the rate of change of a function. If the derivative is positive and the change in x is negative, then the change in y will be negative, reflecting the rule of signs in division.
- Complex Numbers: Even with complex numbers, which involve imaginary units, the fundamental rules of arithmetic operations, including the rules of signs, must be applied consistently.
Conclusion
Dividing a positive number by a negative number consistently yields a negative quotient. This rule is rooted in the fundamental principles of arithmetic, ensuring mathematical coherence. Understanding the inverse relationship between multiplication and division, visualizing the number line, and applying real-world scenarios can help solidify this concept. By avoiding common mistakes and practicing diligently, you can master the rules of signs and perform division operations with confidence. This foundational knowledge is essential for success in higher-level mathematics and practical applications.
Latest Posts
Latest Posts
-
Isoelectric Point Of An Amino Acid
Nov 04, 2025
-
What Does An Odd Function Look Like
Nov 04, 2025
-
Ap Chemistry Unit 1 Practice Test
Nov 04, 2025
-
Slope Intercept Form To Point Slope
Nov 04, 2025
-
Is Initial Momentum Plus A Force Equal To Final Momentum
Nov 04, 2025
Related Post
Thank you for visiting our website which covers about What Is A Positive Divided By A Negative . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.