What Is 9 To The Power Of 0
pinupcasinoyukle
Nov 21, 2025 · 7 min read
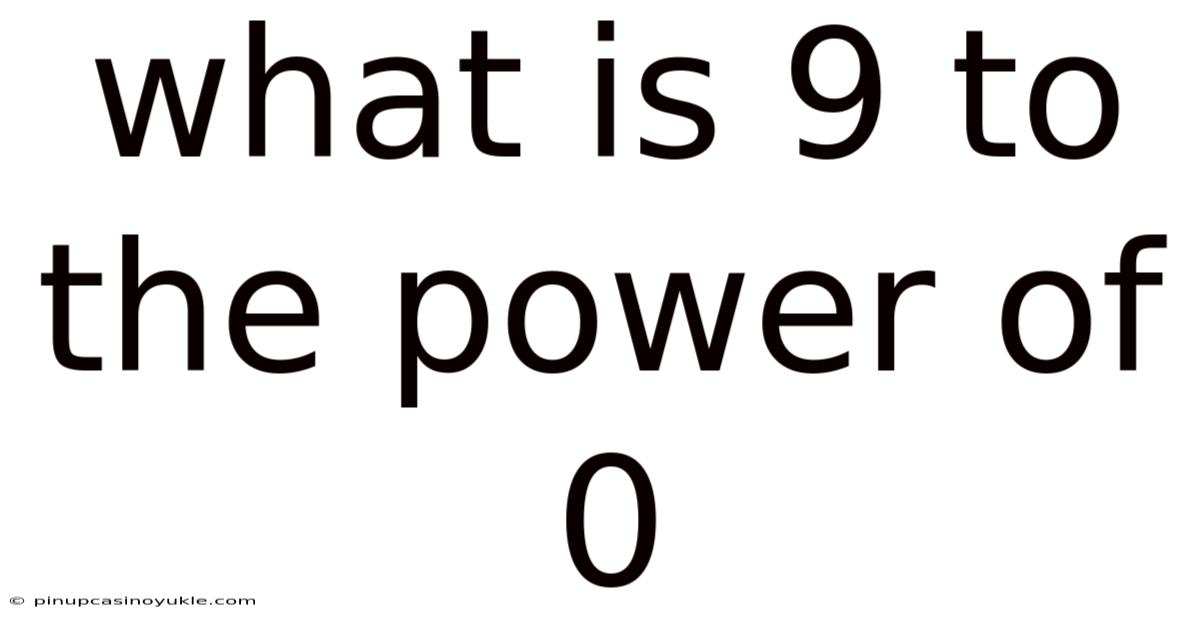
Table of Contents
Raising a number to the power of zero might seem counterintuitive at first glance, but it's a fundamental concept in mathematics with a logical explanation. The expression 9 to the power of 0, written as 9⁰, is a classic example that showcases the elegance and consistency of mathematical rules. This article will explore the definition, reasoning, and implications of any number raised to the power of zero, focusing specifically on why 9⁰ equals 1.
Understanding Exponents
Before diving into why 9⁰ = 1, it's crucial to understand what exponents represent. An exponent, also known as a power, indicates how many times a base number is multiplied by itself. For example:
- 9² (9 to the power of 2) means 9 * 9 = 81
- 9³ (9 to the power of 3) means 9 * 9 * 9 = 729
- 9⁴ (9 to the power of 4) means 9 * 9 * 9 * 9 = 6561
The exponent tells us how many times to use the base number as a factor in the multiplication. This concept is straightforward when dealing with positive integer exponents. However, when we encounter an exponent of 0, the intuitive understanding of repeated multiplication breaks down.
The Zero Exponent Rule
The zero exponent rule states that any non-zero number raised to the power of 0 is equal to 1. Mathematically, this is expressed as:
x⁰ = 1, where x ≠ 0
Therefore, 9⁰ = 1, and this holds true for any other non-zero number as the base. This rule might seem arbitrary, but it's rooted in the consistency of mathematical operations and patterns.
Reasons and Explanations
1. Pattern Continuation
One way to understand why 9⁰ = 1 is to examine the pattern of decreasing exponents. Consider the following sequence:
- 9⁴ = 6561
- 9³ = 729
- 9² = 81
- 9¹ = 9
Notice that each time the exponent decreases by 1, the result is divided by 9.
- 6561 / 9 = 729
- 729 / 9 = 81
- 81 / 9 = 9
Following this pattern, if we decrease the exponent by 1 again, we get:
- 9⁰ = 9 / 9 = 1
This demonstrates that defining 9⁰ as 1 maintains the established pattern and ensures the consistency of exponential operations.
2. Division Rule of Exponents
Another way to justify the zero exponent rule is by using the division rule of exponents. This rule states that when dividing two exponential expressions with the same base, you subtract the exponents:
xᵃ / xᵇ = xᵃ⁻ᵇ
Now, let's consider a case where the exponents are equal, such as dividing 9² by 9²:
- 9² / 9² = 81 / 81 = 1
Using the division rule of exponents:
- 9² / 9² = 9²⁻² = 9⁰
Since 9² / 9² is equal to both 1 and 9⁰, it follows that:
- 9⁰ = 1
This explanation highlights how the zero exponent rule is a natural consequence of the division rule of exponents.
3. Maintaining Mathematical Consistency
Defining 9⁰ as 1 ensures the consistency of other mathematical rules and formulas. For instance, consider the rule for multiplying exponential expressions with the same base:
xᵃ * xᵇ = xᵃ⁺ᵇ
If we want this rule to hold true when one of the exponents is 0, then:
- 9ᵃ * 9⁰ = 9ᵃ⁺⁰ = 9ᵃ
For this equation to be valid, 9⁰ must be equal to 1. If 9⁰ were any other number, it would disrupt this fundamental property of exponents.
4. Combinatorial Explanation
In some contexts, exponents can represent the number of ways to arrange or select items. While this interpretation is more abstract for fractional or negative exponents, it provides an intuitive understanding for the zero exponent.
Consider the question: "In how many ways can you choose 0 items from a set of 9 items?" There is only one way to choose nothing, which is to simply not choose anything. This aligns with the concept that 9⁰ = 1.
Why Not Zero?
It's essential to understand why 9⁰ is defined as 1, and not 0. If 9⁰ were defined as 0, it would create inconsistencies in mathematical operations. As demonstrated earlier, it would disrupt the division rule of exponents and the multiplication rule of exponents. Additionally, it would contradict the pattern of decreasing exponents, where each step involves dividing by the base.
The Case of 0⁰
While any non-zero number raised to the power of 0 is 1, the case of 0⁰ is more complicated. In some contexts, 0⁰ is defined as 1, while in others, it is left undefined. The value of 0⁰ depends on the specific branch of mathematics and the context in which it is used.
-
Calculus: In calculus, 0⁰ is often considered an indeterminate form. This means that the limit of a function of the form f(x)^g(x) as x approaches a certain value, where both f(x) and g(x) approach 0, cannot be determined without further analysis.
-
Combinatorics and Discrete Mathematics: In combinatorics and discrete mathematics, 0⁰ is often defined as 1. This definition simplifies many formulas and theorems in these fields. For example, the binomial theorem and the definition of power series are more consistent when 0⁰ = 1.
-
Computer Science: In some programming languages and software applications, 0⁰ is defined as 1 for consistency and convenience in certain algorithms.
The ambiguity surrounding 0⁰ underscores the importance of context in mathematics. While 9⁰ is unambiguously 1, the value of 0⁰ requires careful consideration based on the specific mathematical domain.
Real-World Applications
Although the concept of raising a number to the power of zero might seem abstract, it has practical applications in various fields, including:
-
Computer Science: Exponents are fundamental in computer science, especially in algorithms related to growth rates, data structures, and complexity analysis. The zero exponent rule ensures that certain algorithms and formulas work correctly.
-
Engineering: Exponents are used extensively in engineering calculations, such as determining the power of electrical circuits, the decay rate of radioactive materials, and the growth of populations.
-
Finance: Exponents are used in finance to calculate compound interest, present value, and future value of investments. The zero exponent rule can simplify certain financial calculations.
-
Physics: Exponents are crucial in physics for describing phenomena such as radioactive decay, wave propagation, and quantum mechanics.
Examples and Practice
To solidify your understanding of the zero exponent rule, consider these examples:
- 5⁰ = 1
- 10⁰ = 1
- (-3)⁰ = 1
- (1/2)⁰ = 1
- √2⁰ = 1
Practice Questions:
- What is the value of 15⁰?
- Simplify the expression: 4² / 4²
- If x ≠ 0, what is the value of (3x)⁰?
Answers:
- 15⁰ = 1
- 4² / 4² = 4²⁻² = 4⁰ = 1
- (3x)⁰ = 1 (as long as x ≠ 0)
Common Misconceptions
-
Confusing x⁰ with 0ˣ: It's important to distinguish between a number raised to the power of 0 (x⁰) and 0 raised to a power (0ˣ). While x⁰ = 1 (for x ≠ 0), 0ˣ = 0 for any positive x.
-
Thinking 9⁰ equals 0: The zero exponent rule states that any non-zero number raised to the power of 0 is 1, not 0.
-
Believing it's an arbitrary rule: The zero exponent rule is not arbitrary; it's a logical consequence of maintaining consistency within mathematical operations and patterns.
Advanced Topics
-
Negative Exponents: A negative exponent indicates the reciprocal of the base raised to the positive exponent. For example, 9⁻¹ = 1/9, 9⁻² = 1/81.
-
Fractional Exponents: A fractional exponent represents a root. For example, 9¹/² = √9 = 3, 9¹/³ = ³√9 ≈ 2.08.
-
Complex Exponents: Exponents can also be complex numbers, leading to more advanced topics in mathematics such as Euler's formula and complex analysis.
Conclusion
The fact that 9⁰ equals 1 is a fundamental concept in mathematics, rooted in the consistency of exponential operations and patterns. Defining any non-zero number raised to the power of 0 as 1 ensures that the division rule of exponents, the multiplication rule of exponents, and other mathematical principles remain valid. While the case of 0⁰ is more complex and context-dependent, the zero exponent rule for non-zero bases is a cornerstone of mathematical reasoning and has practical applications in various fields. Understanding why 9⁰ = 1 is not just about memorizing a rule; it's about appreciating the elegance and interconnectedness of mathematical concepts.
Latest Posts
Latest Posts
-
What Are Two Kinds Of Reproduction
Nov 21, 2025
-
What Is The Scale Factor Of This Dilation
Nov 21, 2025
-
Equation Of A Circle Standard Form
Nov 21, 2025
-
Did The New Deal Actually End The Great Depression
Nov 21, 2025
-
How Do You Calculate Instantaneous Speed
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about What Is 9 To The Power Of 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.