What Is 5 To The Power Of 0
pinupcasinoyukle
Nov 04, 2025 · 8 min read
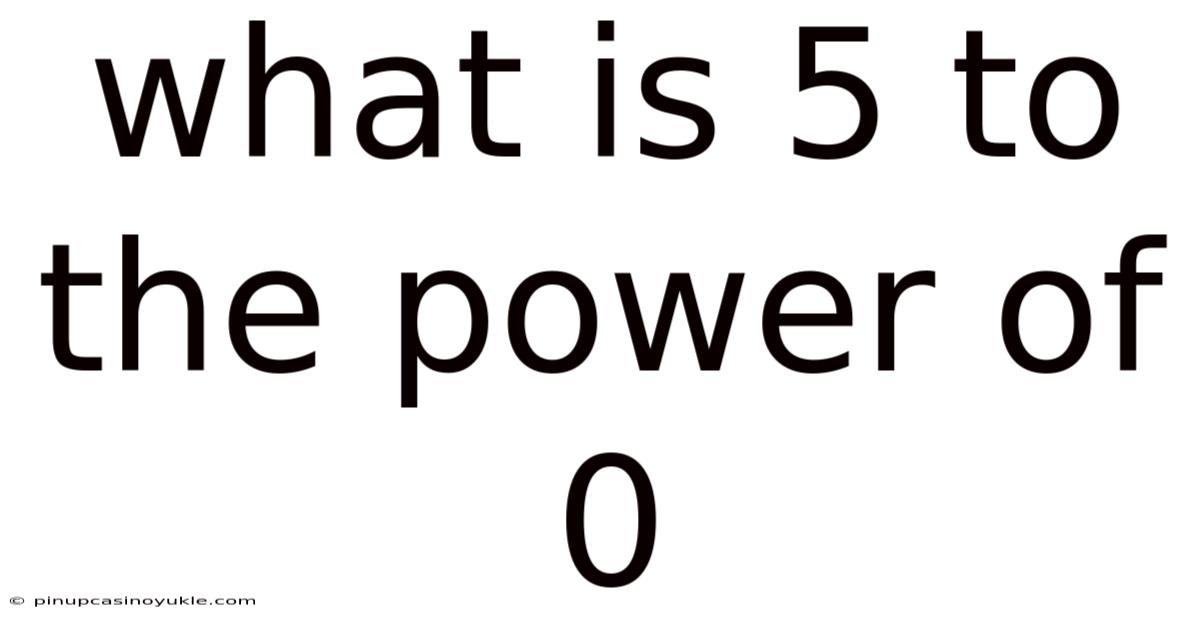
Table of Contents
Raising 5 to the power of 0, or 5⁰, is a mathematical expression that often leads to curiosity and questions. While it might seem intuitive that any number raised to the power of 0 should be 0, the actual answer is 1. This article delves into why this is the case, exploring the mathematical principles and various explanations that support this concept.
The Foundation: Exponents Explained
Before diving into why 5⁰ equals 1, it's essential to understand what exponents represent. An exponent indicates how many times a number (the base) is multiplied by itself. For example, 5³ (5 to the power of 3) means 5 * 5 * 5, which equals 125.
- Base: The number being multiplied (in this case, 5).
- Exponent: The number indicating how many times the base is multiplied by itself (in this case, 3).
So, 5³ = 5 * 5 * 5 = 125. Similarly, 5² = 5 * 5 = 25, and 5¹ = 5. Understanding this foundation is crucial for grasping why 5⁰ = 1.
The Pattern Approach: Decreasing Exponents
One of the simplest ways to understand why 5⁰ = 1 is by observing the pattern that emerges as we decrease the exponent. Let's start with a higher power of 5 and work our way down:
- 5⁴ = 625
- 5³ = 125
- 5² = 25
- 5¹ = 5
Notice that to get from one line to the next, we divide by 5:
- 625 / 5 = 125
- 125 / 5 = 25
- 25 / 5 = 5
If we continue this pattern, the next step would be to divide 5 by 5:
- 5 / 5 = 1
Therefore, following this pattern, 5⁰ should logically equal 1. This approach provides an intuitive understanding based on the consistency of mathematical operations.
The Division Rule of Exponents
Another way to explain why 5⁰ = 1 is by using the division rule of exponents. This rule states that when dividing two exponents with the same base, you subtract the exponents:
a<sup>m</sup> / a<sup>n</sup> = a<sup>m-n</sup>
Let's apply this rule to a situation where we can derive 5⁰:
Consider 5² / 5². We know that any number divided by itself equals 1. So, 5² / 5² = 1.
Now, let's use the division rule of exponents:
- 5² / 5² = 5<sup>2-2</sup> = 5⁰
Since 5² / 5² = 1 and 5² / 5² = 5⁰, it follows that 5⁰ = 1. This approach uses a fundamental rule of exponents to arrive at the same conclusion.
The Identity Property of Multiplication
The identity property of multiplication states that any number multiplied by 1 remains unchanged. In other words, 1 is the multiplicative identity. We can use this property to understand why 5⁰ = 1.
Consider the expression 5¹ = 5. We can rewrite this as:
- 5¹ = 5 * 1
Now, let's introduce 5⁰ into the equation while maintaining the equality. We can write 5 as 5¹ * 5⁰ / 5⁰ because multiplying and dividing by the same quantity (5⁰) doesn't change the value:
- 5 = 5¹ * (5⁰ / 5⁰)
Since 5⁰ / 5⁰ = 1, we have:
- 5 = 5¹ * 1
Comparing this with our original equation, 5¹ = 5 * 1, we can see that 5⁰ must be 1 to maintain the equality.
The General Rule: Anything to the Power of 0
The principle that any non-zero number raised to the power of 0 equals 1 is a general rule in mathematics. This rule is not limited to the number 5; it applies to all numbers except 0. Mathematically, this can be expressed as:
a⁰ = 1, where a ≠ 0
The reason why 0⁰ is undefined is more complex and involves concepts from calculus and limits. For the purpose of this article, we will focus on why non-zero numbers raised to the power of 0 equal 1.
Why Not Zero? The Case of 0⁰
It's important to note that 0⁰ is undefined in most contexts. This is because the behavior of exponents with a base of 0 is inconsistent. In some cases, it might seem logical to define 0⁰ as 0, since 0 raised to any positive power is 0 (e.g., 0¹ = 0, 0² = 0, etc.). However, as we've seen, any non-zero number raised to the power of 0 is 1.
The conflict between these two tendencies leads mathematicians to generally leave 0⁰ undefined. Defining it would create inconsistencies and exceptions in many mathematical rules and theorems. In advanced mathematics, particularly in calculus, the expression 0⁰ is sometimes encountered as a limit, and its value depends on the specific context of the limit.
Applications and Implications
The rule that 5⁰ = 1 (or, more generally, a⁰ = 1) has several applications and implications in various areas of mathematics and science. Here are a few examples:
- Polynomials: In polynomial expressions, the constant term can be thought of as a coefficient multiplied by x⁰. For example, in the polynomial 3x² + 2x + 5, the constant term 5 is actually 5x⁰. Since x⁰ = 1, the constant term remains 5.
- Combinatorics: In combinatorics, the expression n⁰ arises in certain counting problems. For instance, the number of ways to choose 0 elements from a set of n elements is often defined as n⁰, which equals 1. This makes sense because there is one way to choose nothing from a set: do nothing.
- Computer Science: In computer science, particularly in the context of algorithms and data structures, the concept of an empty set or a null operation is often represented mathematically. The idea that anything to the power of 0 is 1 aligns with the notion that performing an operation zero times results in the initial state, which can be considered as "1" in a multiplicative sense.
- Scientific Notation: Scientific notation is used to represent very large or very small numbers. The general form is a × 10<sup>b</sup>, where a is a number between 1 and 10, and b is an integer. When b is 0, we have a × 10⁰, which simplifies to a × 1, or just a. This is useful for representing numbers that are already between 1 and 10.
- Consistency in Mathematical Rules: Perhaps the most important implication is that defining a⁰ = 1 maintains consistency in mathematical rules and theorems. It allows us to extend patterns and formulas without creating unnecessary exceptions.
Common Misconceptions
Despite the clear explanations and justifications, some common misconceptions persist regarding why 5⁰ = 1. Here are a few:
- Anything to the power of 0 is 0: This is a common mistake. The rule that a⁰ = 1 (for a ≠ 0) is often confused with the rule that 0 raised to any positive power is 0 (i.e., 0<sup>n</sup> = 0 for n > 0).
- It's just a convention: While it's true that a⁰ = 1 is a definition, it's not an arbitrary convention. It's a definition that is consistent with other mathematical rules and patterns. As we've seen, there are multiple ways to justify this definition using fundamental principles of mathematics.
- It doesn't make sense: Some people find it counterintuitive that a number raised to the power of 0 should equal 1. This is often because they think of exponents as representing repeated multiplication. While this is true for positive integer exponents, it's important to understand that exponents can also be negative, fractional, or zero, and the rules for these exponents are designed to maintain consistency and coherence in mathematics.
- It only applies to integers: The rule that a⁰ = 1 applies to all real numbers (except 0) and even to complex numbers. The base a can be any number, as long as it's not zero.
Alternative Explanations and Proofs
Beyond the explanations already provided, there are other ways to understand and prove why 5⁰ = 1. Here are a couple of additional approaches:
-
Using Limits: In calculus, the concept of limits can be used to show why a⁰ = 1. Consider the function f(x) = a<sup>x</sup>, where a is a non-zero constant. As x approaches 0, the value of f(x) approaches 1. Mathematically, this can be written as:
lim<sub>x→0</sub> a<sup>x</sup> = 1
This means that as x gets closer and closer to 0, a<sup>x</sup> gets closer and closer to 1. This provides a more rigorous justification for why a⁰ = 1.
-
Using Complex Numbers: In complex analysis, Euler's formula connects exponential functions with trigonometric functions:
e<sup>ix</sup> = cos(x) + i sin(x)
where e is the base of the natural logarithm, i is the imaginary unit, and x is a real number. If we let x = 0, we get:
e<sup>i(0)</sup> = cos(0) + i sin(0)
Since cos(0) = 1 and sin(0) = 0, this simplifies to:
e<sup>0</sup> = 1 + i(0) = 1
This shows that the exponential function with base e raised to the power of 0 equals 1, which is consistent with the general rule.
Conclusion: Embracing the Elegance of Mathematics
Understanding why 5⁰ = 1 (or, more generally, why any non-zero number raised to the power of 0 equals 1) is a journey into the elegance and consistency of mathematics. While it might seem counterintuitive at first, exploring the patterns, rules, and properties of exponents reveals a coherent and logical framework.
From the pattern of decreasing exponents to the division rule of exponents, the identity property of multiplication, and even concepts from calculus and complex analysis, there are multiple ways to understand and justify this fundamental rule.
By embracing these explanations, we can move beyond rote memorization and develop a deeper appreciation for the beauty and interconnectedness of mathematical concepts. The rule that a⁰ = 1 is not just a convention; it's a cornerstone of mathematical consistency and coherence.
Latest Posts
Latest Posts
-
Two Most Imortant Greek City States
Nov 04, 2025
-
How To Turn A Mixed Fraction Into A Decimal
Nov 04, 2025
-
How Do You Subtract Fractions With Different Denominators
Nov 04, 2025
-
How To Get Concentration From Absorbance
Nov 04, 2025
-
What Do Mitochondria Do In Plant Cells
Nov 04, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 To The Power Of 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.