What Is 4 To The 0 Power
pinupcasinoyukle
Nov 17, 2025 · 9 min read
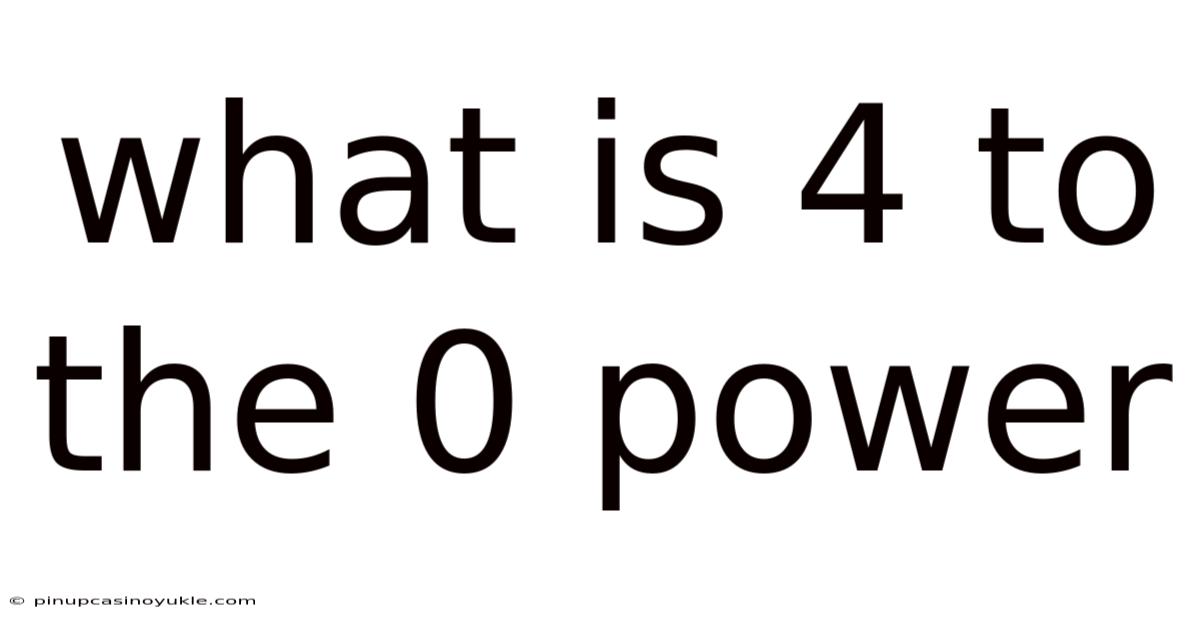
Table of Contents
The enigma of exponents takes an intriguing turn when we encounter 4 to the 0 power, a mathematical expression that often sparks curiosity and a quest for deeper understanding. This seemingly simple concept opens the door to a world of mathematical principles, unveiling the elegance and consistency that underpin the language of numbers.
The Foundation: Understanding Exponents
At its core, an exponent signifies repeated multiplication. For instance, 4 to the power of 3 (written as 4³) means multiplying 4 by itself three times: 4 x 4 x 4, which equals 64. The base (4 in this case) is the number being multiplied, and the exponent (3) indicates how many times the base is multiplied by itself. This basic understanding forms the groundwork for comprehending more complex exponential concepts, including the curious case of zero exponents.
The Zero Exponent: A Definition
Any non-zero number raised to the power of 0 is equal to 1. Therefore, 4⁰ = 1. This isn't just a convention; it's a fundamental rule that ensures the consistency and coherence of mathematical operations. Understanding why this is true requires exploring the properties of exponents and their relationship to division.
Why is 4⁰ = 1? The Mathematical Reasoning
Several approaches help illustrate the logic behind this rule:
-
The Division Property of Exponents: This property states that when dividing two exponents with the same base, you subtract the exponents. For example, 4³/4² = 4^(3-2) = 4¹ = 4. Now, consider 4¹/4¹: according to the division property, this equals 4^(1-1) = 4⁰. However, any number divided by itself is 1. Thus, 4¹/4¹ = 1, and since 4¹/4¹ also equals 4⁰, it follows that 4⁰ = 1.
-
Maintaining Patterns: Exponents follow a clear pattern. Consider the powers of 4:
- 4⁴ = 256
- 4³ = 64
- 4² = 16
- 4¹ = 4
Notice that as the exponent decreases by 1, the result is divided by 4. To maintain this pattern, the next step would be 4⁰, which should equal 4/4 = 1. This pattern-based reasoning reinforces the idea that 4⁰ must be 1 to preserve mathematical consistency.
-
The Multiplicative Identity: The number 1 is the multiplicative identity, meaning any number multiplied by 1 remains unchanged. Exponents, especially in the context of powers, are fundamentally about multiplication. Raising a number to the power of 0 can be seen as a way to maintain the original value without changing it through multiplication.
Real-World Applications and Implications
While the concept of 4⁰ = 1 might seem abstract, it has practical implications in various fields:
-
Computer Science: In programming, exponents are used extensively in algorithms for calculations, data analysis, and more. The concept of a zero exponent is crucial for handling edge cases and ensuring the accuracy of computations.
-
Physics: Exponential functions are used to model various phenomena, such as radioactive decay and compound interest. Understanding the role of zero exponents is vital for accurately interpreting these models.
-
Engineering: Engineers use exponents in designing structures, calculating loads, and modeling systems. Zero exponents can appear in equations that describe initial conditions or steady-state scenarios.
Common Misconceptions
-
Anything to the power of zero is zero: This is a common mistake. Only 0 to the power of any positive number is zero (0^n = 0 for n > 0). However, any non-zero number to the power of zero is 1.
-
Zero to the power of zero is one: This is a more nuanced issue. In many contexts, 0⁰ is undefined. However, in some specific scenarios, such as combinatorics or set theory, it's convenient to define 0⁰ as 1. This is a topic of debate among mathematicians, and the appropriate definition depends on the context.
Examples and Exercises
To solidify your understanding, consider these examples:
- 5⁰ = 1
- 10⁰ = 1
- (-3)⁰ = 1
- (1/2)⁰ = 1
Exercises:
- What is the value of (7⁰ + 3⁰) * 2?
- Simplify the expression: (x^2 * y^3)⁰, assuming x and y are non-zero.
- Calculate: 2⁴ / 2⁴
Answers:
- (1 + 1) * 2 = 4
- 1
- 1
Advanced Considerations
-
Complex Numbers: The rule extends to complex numbers as well. If z is a complex number (other than 0), then z⁰ = 1.
-
Functions: In calculus and analysis, exponential functions like eˣ are foundational. The value of e⁰ = 1 is a cornerstone in understanding the properties and behavior of these functions.
The Historical Perspective
The development of exponential notation and the understanding of zero exponents evolved over centuries. Early mathematicians grappled with defining and interpreting these concepts, eventually leading to the modern understanding that ensures mathematical consistency.
Conclusion
The concept of 4 to the 0 power, or any non-zero number raised to the power of 0, equalling 1, is a fundamental principle in mathematics. It's not just a rule; it's a consequence of maintaining the consistency and coherence of exponential operations. By understanding the mathematical reasoning, real-world applications, and historical context, we gain a deeper appreciation for the elegance and precision of mathematics.
Delving Deeper into Exponents: Beyond the Basics
The exploration of exponents and the peculiar case of zero as an exponent opens up a fascinating avenue to comprehend more advanced mathematical concepts. It is not just about memorizing a rule but understanding the underlying principles that make mathematics a logical and consistent system. Here, we expand on the initial premise and explore related ideas, addressing potential nuances and further applications.
Zero as an Exponent: Addressing the Nuances
The idea that any non-zero number to the power of zero equals one is straightforward, but it's worth addressing some of the more subtle aspects and potential pitfalls.
The Case of 0⁰: An Undefined Territory?
One of the most debated topics in mathematics is the value of 0⁰. Unlike any non-zero number raised to the power of zero, which is definitively 1, the expression 0⁰ is often considered undefined. This ambiguity arises because the rules governing exponents and the properties of zero create conflicting expectations.
-
Conflicting Intuitions: On one hand, following the pattern of exponents, we might expect 0⁰ to be 1, similar to how 4⁰ = 1, 5⁰ = 1, and so on. On the other hand, any power of zero is typically zero (0², 0³, 0⁴,... are all zero), leading us to believe 0⁰ should be zero.
-
Context Matters: The definition of 0⁰ can depend on the specific context. In some areas of mathematics, especially those involving limits and calculus, leaving 0⁰ undefined is more convenient. In other fields, such as combinatorics or set theory, defining 0⁰ as 1 simplifies many formulas and theorems. For example, in the binomial theorem, defining 0⁰ as 1 allows the theorem to hold for all values of the variables.
-
Practical Implications: In computational systems, the way 0⁰ is handled can vary. Some software or programming languages may return an error, while others might default to 1. Therefore, it's crucial to be aware of how the specific tools you are using handle this edge case.
Negative Exponents: Another Perspective
Understanding negative exponents complements the knowledge of zero exponents. A negative exponent indicates the reciprocal of the base raised to the positive exponent.
-
Definition: If n is a positive integer, then x⁻ⁿ = 1/xⁿ, where x is a non-zero number.
-
Example: 4⁻² = 1/4² = 1/16.
-
Why it Works: Negative exponents help maintain the consistency of exponential rules. Consider the division rule: xᵃ/xᵇ = x^(ᵃ⁻ᵇ). If a is less than b, the exponent becomes negative. For instance, 4²/4⁴ = 4^(2-4) = 4⁻². But 4²/4⁴ also equals 1/4², demonstrating that 4⁻² = 1/4².
Fractional Exponents: Unveiling Roots
Fractional exponents connect exponents to radicals or roots. An exponent of the form 1/n indicates the n-th root of the base.
-
Definition: x^(1/n) = ⁿ√x, where x is a non-negative number and n is a positive integer.
-
Example: 4^(1/2) = √4 = 2.
-
General Fractional Exponents: For a general fractional exponent m/n, x^(m/n) = (ⁿ√x)*ᵐ.
-
Example: 4^(3/2) = (√4)³ = 2³ = 8.
Exponential Functions: Beyond Numerical Values
Exponential functions are functions where the variable appears in the exponent. They are crucial in modeling various real-world phenomena.
-
General Form: f(x) = aᵇˣ, where a is a non-zero constant, and b is the base of the exponent.
-
Examples:
- f(x) = 2ˣ (exponential growth)
- f(x) = (1/2)ˣ (exponential decay)
- f(x) = eˣ (the natural exponential function, where e is Euler's number, approximately 2.71828)
-
Applications: Exponential functions are used in:
- Finance: Modeling compound interest.
- Biology: Modeling population growth.
- Physics: Modeling radioactive decay.
- Computer Science: Analyzing algorithms.
Logarithms: The Inverse of Exponents
Logarithms are the inverse of exponential functions. The logarithm of a number x to the base b is the exponent to which b must be raised to equal x.
-
Definition: If bʸ = x, then logb(x) = y.
-
Examples:
- log₂ (8) = 3, because 2³ = 8.
- log₁₀ (100) = 2, because 10² = 100.
- ln(e) = 1, where ln is the natural logarithm (base e), because e¹ = e.
-
Properties: Logarithms have several useful properties that make them valuable in solving exponential equations and simplifying complex expressions.
- logb(xy) = logb(x) + logb(y)
- logb(x/y) = logb(x) - logb(y)
- logb(xⁿ) = n logb(x)
Advanced Examples and Applications
To further illustrate the applications of these concepts, consider the following examples:
-
Compound Interest: The formula for compound interest is A = P(1 + r/n)^(nt), where:
- A is the future value of the investment/loan, including interest.
- P is the principal investment amount (the initial deposit or loan amount).
- r is the annual interest rate (as a decimal).
- n is the number of times that interest is compounded per year.
- t is the number of years the money is invested or borrowed for.
Understanding exponents is crucial in calculating the future value of an investment.
-
Radioactive Decay: The amount of a radioactive substance remaining after time t is given by N(t) = N₀ e^(−λt), where:
- N(t) is the amount of the substance remaining at time t.
- N₀ is the initial amount of the substance.
- λ is the decay constant.
- e is the base of the natural logarithm.
Here, the exponential function models the decay process, and understanding exponents is essential for predicting the amount of substance remaining after a certain period.
-
Algorithm Analysis: In computer science, the efficiency of algorithms is often analyzed using Big O notation, which involves exponential and logarithmic functions. For example, an algorithm with a time complexity of O(2ⁿ) has an execution time that grows exponentially with the input size n.
Conclusion: The Ubiquitous Nature of Exponents
Exponents, including the special case of zero exponents, are not just abstract mathematical concepts. They are fundamental tools that underpin a wide range of scientific, engineering, and computational disciplines. By understanding the rules and properties of exponents, we unlock the ability to model and analyze complex phenomena, solve intricate problems, and gain deeper insights into the world around us. From finance to physics, and from computer science to engineering, exponents provide a powerful language for describing change, growth, and relationships. The journey from understanding 4⁰ = 1 to comprehending exponential functions and logarithms is a testament to the interconnectedness and elegance of mathematics.
Latest Posts
Latest Posts
-
Find The Lengths Of The Missing Sides In The Triangle
Nov 17, 2025
-
Math Words That Start With U
Nov 17, 2025
-
What Is The End Product Of Glycolysis
Nov 17, 2025
-
How To Convert Mixed Fraction To Improper Fraction
Nov 17, 2025
-
What Are The Informal Powers Of The President
Nov 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 To The 0 Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.