What Is 25 Divided By 2
pinupcasinoyukle
Nov 17, 2025 · 9 min read
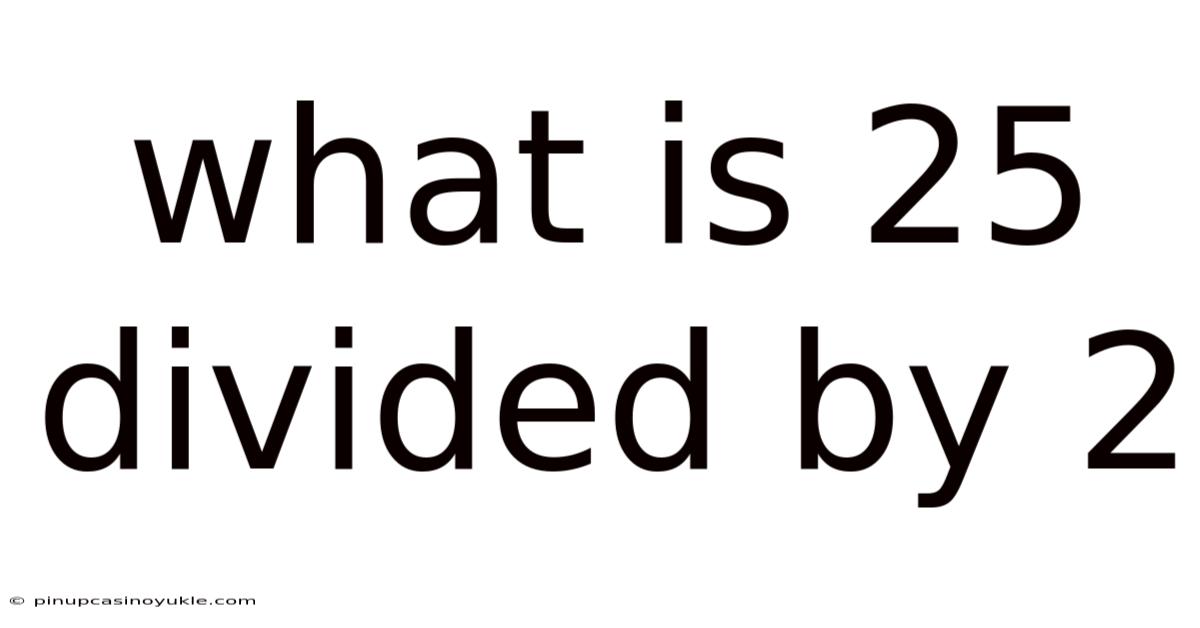
Table of Contents
Dividing 25 by 2 is a fundamental arithmetic operation that yields a result crucial for various real-world applications, from splitting a restaurant bill to understanding proportions in scientific research. This seemingly simple calculation provides a gateway to more complex mathematical concepts and enhances our problem-solving skills.
The Basics of Division
Division, one of the four basic arithmetic operations, involves splitting a number (the dividend) into equal parts, as defined by another number (the divisor). In our case, 25 is the dividend, and 2 is the divisor. The result of the division is called the quotient.
- Dividend: The number being divided (25).
- Divisor: The number by which the dividend is divided (2).
- Quotient: The result of the division.
Performing the Division: 25 ÷ 2
To divide 25 by 2, we need to determine how many times 2 fits into 25. This can be done through long division or simply by recognizing that 25 is an odd number, and dividing it by 2 will result in a whole number and a remainder, or a decimal.
Here's how we can perform the division:
- Whole Number Quotient:
- 2 goes into 2 twice (2 x 1 = 2), so we can estimate how many times 2 goes into 25.
- 2 goes into 20 ten times (2 x 10 = 20).
- We have 5 left (25 - 20 = 5).
- 2 goes into 5 twice (2 x 2 = 4).
- So, 2 goes into 25 a total of 10 + 2 = 12 times.
- Remainder:
- After 2 goes into 25 twelve times, we have 1 left over (25 - (2 x 12) = 1).
- This means the remainder is 1.
- Expressing as a Mixed Number:
- The result can be expressed as a mixed number: 12 1/2.
- Expressing as a Decimal:
- To convert the remainder to a decimal, we divide the remainder (1) by the divisor (2).
- 1 ÷ 2 = 0.5
- Therefore, 25 ÷ 2 = 12.5
Understanding the Result: 12.5
The result of 25 divided by 2 is 12.5. This means that if you split 25 into two equal parts, each part would be 12.5. This decimal value represents a precise division, crucial for accurate calculations in various applications.
Real-World Applications
The simple calculation of 25 divided by 2 has numerous practical applications in everyday life:
-
Splitting a Bill: Imagine you and a friend have a restaurant bill of $25 and decide to split it equally. Each person would owe $12.50.
-
Cooking and Baking: If a recipe calls for a certain amount of an ingredient but you only want to make half the recipe, and the original recipe requires 25 ounces of flour, you would need 12.5 ounces.
-
Measuring and Construction: Suppose you need to cut a 25-inch piece of wood into two equal lengths. Each piece would be 12.5 inches long.
-
Calculating Averages: If you have two test scores totaling 25 points and want to find the average score, you would divide 25 by 2, resulting in an average score of 12.5.
-
Financial Planning: If you have $25 to invest and want to allocate it equally between two different stocks, you would invest $12.50 in each stock.
The Significance of Remainders
When dividing numbers, especially in whole number arithmetic, understanding remainders is crucial. The remainder represents the amount "left over" after performing the division as many times as possible with whole numbers.
In the case of 25 ÷ 2, the remainder is 1. This means that after dividing 25 by 2 twelve times, there is still 1 unit that couldn't be equally divided. The remainder can be expressed as a fraction of the divisor (1/2) or converted into a decimal (0.5), allowing for a more precise answer.
Understanding remainders is particularly important in scenarios where only whole numbers make sense, such as distributing items among people or dividing objects.
Decimal Representation and Precision
The decimal representation of 25 ÷ 2 (12.5) provides a level of precision that whole numbers and remainders alone cannot offer. Decimals are an extension of the base-10 number system, allowing us to express fractional parts of a whole.
In the context of 12.5, the ".5" represents half of a unit. This precise representation is essential in fields like science, engineering, and finance, where accuracy is paramount.
Alternative Methods of Calculation
While long division is a standard method, there are alternative ways to calculate 25 ÷ 2:
-
Repeated Subtraction: Subtract 2 from 25 repeatedly until you can no longer subtract 2 without going into negative numbers. Count how many times you subtracted 2 (12 times), and the remaining number is the remainder (1).
-
Using a Calculator: Simply enter 25 ÷ 2 into a calculator to get the result 12.5.
-
Mental Math: Break down 25 into smaller, manageable parts. For example, 20 ÷ 2 = 10 and 5 ÷ 2 = 2.5. Then, add the results: 10 + 2.5 = 12.5.
Advanced Applications
Beyond simple calculations, the principles of division are fundamental to more advanced mathematical and scientific concepts:
-
Ratios and Proportions: Division is used to calculate ratios and proportions, which are essential in fields like chemistry (calculating molar ratios) and physics (determining proportional relationships between variables).
-
Statistics: Division is used to calculate means (averages), which are a fundamental statistical measure. For example, dividing the sum of a set of numbers by the count of numbers gives the average.
-
Calculus: Division is integral to understanding derivatives and integrals, which are core concepts in calculus. Derivatives involve finding the rate of change by dividing the change in one variable by the change in another.
-
Computer Science: Division is used in algorithms for tasks like data partitioning, load balancing, and calculating hash values.
Common Mistakes to Avoid
When performing division, it's easy to make mistakes. Here are some common pitfalls to avoid:
-
Misunderstanding the Remainder: Not understanding that the remainder represents the amount "left over" after division can lead to incorrect interpretations of the result.
-
Incorrect Decimal Placement: When converting remainders to decimals, ensure you place the decimal point correctly.
-
Calculation Errors: Simple arithmetic errors can lead to incorrect results. Always double-check your calculations.
-
Forgetting the Order of Operations: In more complex equations, remember to follow the order of operations (PEMDAS/BODMAS) to ensure correct calculations.
Historical Perspective
Division has been a fundamental arithmetic operation since ancient times. Early civilizations like the Babylonians and Egyptians developed methods for dividing numbers, often using tables and algorithms to aid in calculations.
The modern notation for division, using the division symbol (÷) or the fraction bar (/), evolved over centuries. The development of efficient division techniques has been crucial for advancements in mathematics, science, and engineering.
The Role of Division in Problem-Solving
Division is not just a mathematical operation; it's a powerful problem-solving tool. It allows us to break down complex problems into smaller, manageable parts, making them easier to understand and solve.
By understanding division, we can analyze data, make informed decisions, and solve practical problems in various aspects of life. Whether it's splitting a bill, calculating proportions, or analyzing statistical data, division is an essential skill for effective problem-solving.
Division in Different Number Systems
While we commonly perform division in the base-10 number system, it's important to note that division can be performed in other number systems as well, such as binary (base-2), octal (base-8), and hexadecimal (base-16).
In computer science, binary division is particularly important because computers use binary code to perform calculations. The principles of division remain the same, but the specific techniques may vary depending on the number system.
Division and its Inverse Operation: Multiplication
Division and multiplication are inverse operations, meaning that one "undoes" the other. If 25 ÷ 2 = 12.5, then 12.5 x 2 = 25. Understanding this relationship is crucial for verifying the accuracy of division calculations.
By using multiplication to check division, you can ensure that the quotient, when multiplied by the divisor, equals the dividend. This principle is fundamental to understanding the relationship between these two arithmetic operations.
Division with Negative Numbers
When dividing negative numbers, the rules of signs apply:
- A positive number divided by a positive number yields a positive result.
- A negative number divided by a negative number yields a positive result.
- A positive number divided by a negative number yields a negative result.
- A negative number divided by a positive number yields a negative result.
For example:
- (-25) ÷ (-2) = 12.5
- 25 ÷ (-2) = -12.5
- (-25) ÷ 2 = -12.5
Estimating Division Results
In many situations, it's useful to estimate the result of a division problem without performing precise calculations. Estimating can help you quickly assess the reasonableness of an answer or make quick decisions in everyday life.
For example, when dividing 25 by 2, you can estimate that 2 goes into 25 about 12 or 13 times. This quick estimate can be useful when you don't have access to a calculator or need to make a quick calculation.
Division and Fractions
Division is closely related to fractions. A fraction represents a part of a whole, and dividing one number by another is equivalent to expressing the division as a fraction.
For example, 25 ÷ 2 can be expressed as the fraction 25/2. This fraction can then be simplified or converted to a mixed number (12 1/2) or a decimal (12.5).
Understanding the relationship between division and fractions is crucial for working with proportions, ratios, and other mathematical concepts.
The Importance of Practice
Like any mathematical skill, mastering division requires practice. By regularly practicing division problems, you can improve your speed, accuracy, and confidence in performing these calculations.
There are many resources available for practicing division, including textbooks, online tutorials, and interactive exercises. By dedicating time to practice, you can strengthen your understanding of division and improve your overall mathematical skills.
Conclusion
The seemingly simple division of 25 by 2 is a gateway to understanding fundamental arithmetic principles and their real-world applications. This calculation illustrates the importance of division in splitting quantities, understanding remainders, and using decimals for precision. From everyday tasks like splitting a bill to advanced applications in science and engineering, division is an essential skill for problem-solving and decision-making. By understanding the basics of division, avoiding common mistakes, and practicing regularly, you can master this fundamental arithmetic operation and unlock its full potential.
Latest Posts
Latest Posts
-
Neutrons Have Which Type Of Electrical Charge
Nov 17, 2025
-
How To Find Axis Of Symmetry Parabola
Nov 17, 2025
-
What Is 1 X 1 X
Nov 17, 2025
-
How To Simplify Radicals With Variables
Nov 17, 2025
-
What Is A Short Run Equilibrium
Nov 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.