What Is 12 Out Of 16 As A Percentage
pinupcasinoyukle
Nov 21, 2025 · 9 min read
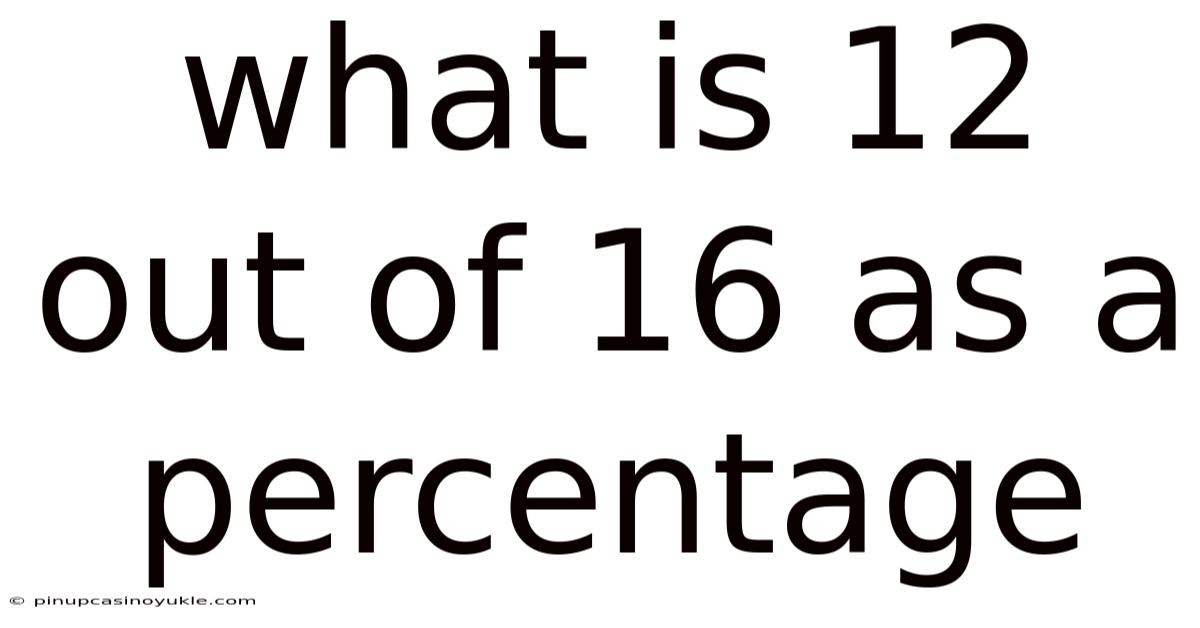
Table of Contents
Calculating percentages is a fundamental skill applicable across various fields, from academic grading to financial analysis. Understanding how to convert fractions into percentages provides a clear, standardized way to interpret proportions and make comparisons. In this article, we will delve into the process of calculating what 12 out of 16 is as a percentage, exploring different methods and contextual applications to enhance your understanding and proficiency.
Understanding the Basics of Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin "per centum," meaning "out of one hundred." Therefore, when we say a percentage, we are essentially stating how many parts out of 100 we have.
Percentages are used to express:
- Ratios: Comparing one quantity to another.
- Changes: Representing increases or decreases.
- Distributions: Showing parts of a whole.
Converting a fraction to a percentage involves scaling the fraction so that its denominator becomes 100. This conversion allows for easy comparison and understanding of proportions.
Converting 12/16 to a Percentage: Step-by-Step
To find what 12 out of 16 is as a percentage, we need to convert the fraction 12/16 into a percentage. Here’s a step-by-step guide:
Step 1: Simplify the Fraction (Optional)
Simplifying the fraction before converting it to a percentage can make the calculation easier. The fraction 12/16 can be simplified by finding the greatest common divisor (GCD) of 12 and 16.
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 16: 1, 2, 4, 8, 16
The GCD of 12 and 16 is 4. Divide both the numerator and the denominator by 4:
- 12 ÷ 4 = 3
- 16 ÷ 4 = 4
So, the simplified fraction is 3/4.
Step 2: Convert the Fraction to a Decimal
To convert a fraction to a decimal, divide the numerator by the denominator:
- 3 ÷ 4 = 0.75
Alternatively, if you started with 12/16:
- 12 ÷ 16 = 0.75
Step 3: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100:
-
- 75 × 100 = 75
Therefore, 12 out of 16 is equal to 75%.
Alternative Methods to Calculate Percentages
Besides the step-by-step method, there are alternative approaches to calculating percentages that can be useful depending on the context and available tools.
Method 1: Direct Proportion
This method involves setting up a proportion to find the percentage directly. The proportion is based on the idea that the fraction is equivalent to a certain percentage out of 100.
-
Set up the proportion:
- 12/16 = x/100
-
Cross-multiply:
- 12 × 100 = 16 × x
- 1200 = 16x
-
Solve for x:
- x = 1200 ÷ 16
- x = 75
Thus, 12 out of 16 is 75%.
Method 2: Using a Calculator
Calculators provide a quick and efficient way to convert fractions to percentages.
-
Divide the numerator by the denominator:
- 12 ÷ 16 = 0.75
-
Multiply by 100:
-
- 75 × 100 = 75
-
The calculator directly gives the percentage as 75%.
Method 3: Percentage Formula
The percentage formula is a straightforward way to calculate percentages:
- Percentage = (Part / Whole) × 100
In this case:
- Part = 12
- Whole = 16
- Percentage = (12 / 16) × 100
- Percentage = 0.75 × 100
- Percentage = 75%
Practical Applications of Calculating Percentages
Understanding how to calculate percentages is valuable in many real-world scenarios. Here are some practical applications:
Academic Grading
In education, percentages are used to represent student performance. For example, if a student scores 12 out of 16 on a test, their score is 75%. This allows teachers to easily compare student performance across different assignments and tests.
- Example: A student gets 12 questions correct out of 16 on a quiz. The percentage score is 75%, which might translate to a letter grade like C or B, depending on the grading scale.
Financial Analysis
Percentages are crucial in finance for analyzing investment returns, interest rates, and financial ratios. For instance, calculating the percentage change in stock prices or sales figures provides insights into performance and trends.
- Example: If a stock portfolio increases in value from $16,000 to $17,200, the increase is $1,200. The percentage increase is ($1,200 / $16,000) × 100 = 7.5%.
Retail and Sales
Retailers use percentages to calculate discounts, markups, and profit margins. Understanding these calculations helps businesses make informed decisions about pricing and inventory.
- Example: An item originally priced at $16 is discounted by $4, resulting in a sale price of $12. The discount percentage is ($4 / $16) × 100 = 25%.
Data Analysis
In data analysis, percentages are used to represent proportions and distributions within datasets. This is essential for interpreting survey results, market trends, and demographic data.
- Example: In a survey of 16 people, 12 prefer a particular brand. The percentage of people who prefer the brand is (12 / 16) × 100 = 75%.
Health and Nutrition
Percentages are used to understand nutritional information, such as the percentage of daily recommended intake in food products.
- Example: A food label indicates that a serving provides 12 grams of fat out of a recommended daily intake of 16 grams. The percentage of daily fat intake is (12 / 16) × 100 = 75%.
Common Mistakes to Avoid When Calculating Percentages
Calculating percentages accurately requires attention to detail. Here are some common mistakes to avoid:
Misidentifying the Base (Whole)
One of the most common errors is using the wrong number as the base or whole. The base is the total quantity from which the percentage is being calculated.
- Mistake: Calculating the percentage increase using the final value instead of the initial value.
- Correct: Ensure that the base is the original or total value before any changes or calculations.
Incorrectly Converting Decimals
When converting decimals to percentages, ensure that you multiply by 100 correctly. Moving the decimal point the wrong way or forgetting to multiply can lead to significant errors.
- Mistake: Converting 0.75 to 7.5% instead of 75%.
- Correct: Always multiply the decimal by 100 to get the correct percentage.
Rounding Errors
Rounding numbers too early in the calculation can lead to inaccuracies in the final percentage.
- Mistake: Rounding 12/16 to 0.7 before multiplying by 100, resulting in 70% instead of 75%.
- Correct: Perform the division to at least two decimal places and round only at the final step.
Forgetting to Simplify Fractions
While not always necessary, failing to simplify fractions can make calculations more complex and prone to error.
- Mistake: Working with the fraction 12/16 instead of simplifying it to 3/4.
- Correct: Simplify fractions to their lowest terms before converting to decimals or percentages.
Misinterpreting Percentage Change
When calculating percentage change, ensure that you understand whether the change is an increase or a decrease and apply the appropriate formula.
- Mistake: Using the wrong formula for percentage increase or decrease.
- Correct: Use the formula: ((New Value - Old Value) / Old Value) × 100. A positive result indicates an increase, while a negative result indicates a decrease.
Advanced Percentage Calculations
Beyond basic conversions, understanding advanced percentage calculations can be useful in more complex scenarios.
Percentage Increase and Decrease
To calculate the percentage increase or decrease between two values, use the following formulas:
- Percentage Increase: (((New Value - Old Value) / Old Value) × 100)
- Percentage Decrease: (((Old Value - New Value) / Old Value) × 100)
For example, if a price increases from $16 to $20:
- Percentage Increase = ((20 - 16) / 16) × 100 = (4 / 16) × 100 = 25%
If a price decreases from $16 to $12:
- Percentage Decrease = ((16 - 12) / 16) × 100 = (4 / 16) × 100 = 25%
Calculating Percentage of a Percentage
Sometimes, you need to find a percentage of a percentage. For example, finding 10% of 50%.
-
Convert both percentages to decimals:
- 10% = 0.10
- 50% = 0.50
-
Multiply the decimals:
-
- 10 × 0.50 = 0.05
-
-
Convert the result back to a percentage:
-
- 05 × 100 = 5%
-
Therefore, 10% of 50% is 5%.
Reverse Percentage Calculations
Reverse percentage calculations involve finding the original value when you know a percentage of it. For example, if 20% of a number is 40, what is the original number?
-
Set up the equation:
-
- 20 × x = 40
-
-
Solve for x:
- x = 40 / 0.20
- x = 200
Therefore, the original number is 200.
The Importance of Understanding Percentages
Mastering percentage calculations is not just an academic exercise; it's a crucial skill that enhances decision-making in various aspects of life. From managing personal finances to understanding complex data, the ability to work with percentages provides a clear and concise way to interpret information.
Financial Literacy
Understanding percentages is essential for financial literacy. Whether you are calculating interest on a loan, determining investment returns, or budgeting your expenses, percentages help you make informed financial decisions.
- Budgeting: Calculating the percentage of your income spent on different categories (e.g., housing, food, transportation) helps you understand your spending habits and identify areas where you can save money.
- Investing: Understanding percentage returns on investments allows you to compare different investment options and assess their potential profitability.
Informed Decision-Making
Percentages provide a standardized way to compare different options and make informed decisions. Whether you are evaluating discounts while shopping, comparing prices, or analyzing data, percentages help you see the relative differences and make rational choices.
- Shopping: Comparing discounts using percentages helps you determine which offer provides the best value. For example, a 20% discount on a $100 item saves you $20, while a 30% discount on a $60 item saves you $18.
- Health: Understanding nutritional information in percentages helps you make healthier food choices. Comparing the percentage of daily recommended intake for different nutrients allows you to balance your diet effectively.
Professional Advancement
In many professions, the ability to work with percentages is a valuable asset. Whether you are analyzing sales data, interpreting market trends, or presenting financial reports, a solid understanding of percentages can enhance your professional credibility and effectiveness.
- Marketing: Analyzing the percentage increase in sales after a marketing campaign helps you evaluate the campaign’s success and make data-driven decisions for future strategies.
- Management: Understanding percentage changes in key performance indicators (KPIs) allows you to track progress towards goals and identify areas that need improvement.
Conclusion
Converting 12 out of 16 to a percentage is a straightforward process that involves converting the fraction to a decimal and then multiplying by 100. The result, 75%, provides a clear understanding of the proportion. Mastering this skill and understanding the various applications of percentages can significantly enhance your ability to analyze data, make informed decisions, and navigate various real-world scenarios. By avoiding common mistakes and practicing regularly, you can become proficient in percentage calculations and leverage this skill to your advantage.
Latest Posts
Latest Posts
-
What Happens When You Minus A Negative Number
Nov 21, 2025
-
How To Simplify The Square Root Of
Nov 21, 2025
-
Social Darwinism Ap World History Definition
Nov 21, 2025
-
What Is The Space Between Neurons Called
Nov 21, 2025
-
How To Find Slope Of A Table
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about What Is 12 Out Of 16 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.