What Is 10 To The Power Of 0
pinupcasinoyukle
Nov 17, 2025 · 7 min read
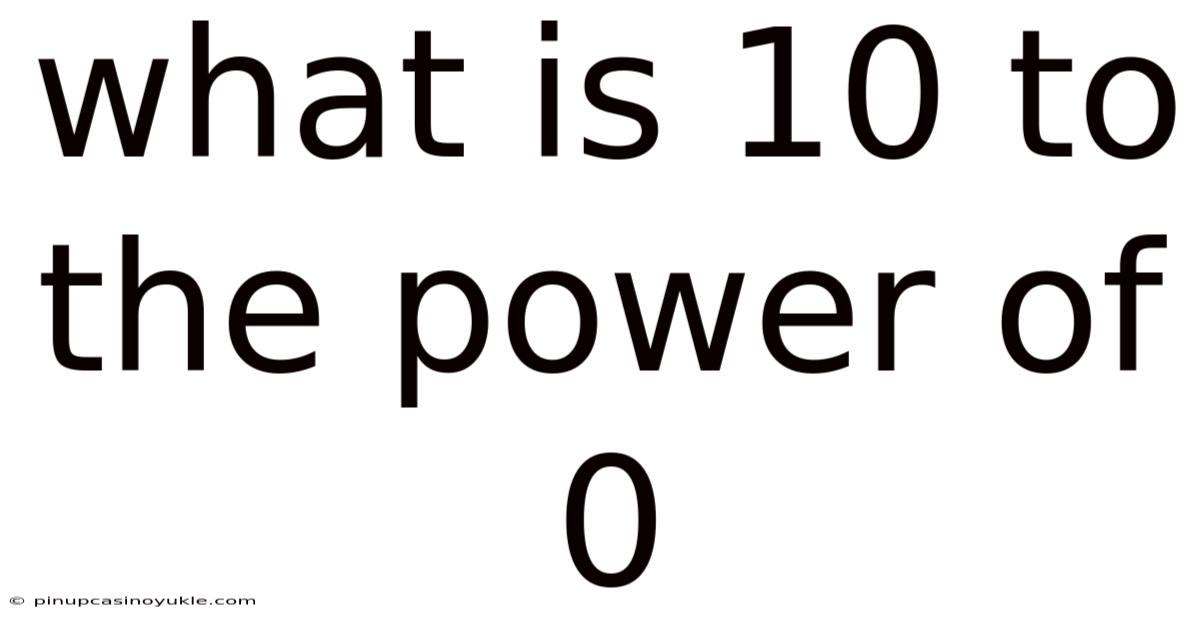
Table of Contents
Raising 10 to the power of 0 might seem puzzling at first glance, especially if you're used to exponents representing repeated multiplication. However, understanding this concept is crucial for grasping more advanced mathematical principles. This article will delve into why 10 to the power of 0, or any non-zero number to the power of 0, equals 1. We will explore the mathematical rules and reasoning behind this seemingly simple yet fundamental concept.
The Foundation: Understanding Exponents
Before we dive into 10 to the power of 0, let's solidify our understanding of exponents. An exponent indicates how many times a base number is multiplied by itself.
- Example: 10<sup>3</sup> means 10 * 10 * 10, which equals 1000.
- In this case, 10 is the base, and 3 is the exponent.
Exponents provide a concise way to represent repeated multiplication, making it easier to express very large or very small numbers. The rules that govern exponents are crucial for simplifying expressions and solving equations. These rules are built upon the fundamental principle of repeated multiplication and allow for efficient manipulation of exponential expressions.
Exploring the Pattern: Powers of 10
Let's examine the powers of 10 as the exponent decreases:
- 10<sup>4</sup> = 10,000
- 10<sup>3</sup> = 1,000
- 10<sup>2</sup> = 100
- 10<sup>1</sup> = 10
Notice a pattern? Each time the exponent decreases by 1, the result is divided by 10. This pattern is consistent and provides a visual understanding of how exponents work. Now, if we continue this pattern:
- 10<sup>0</sup> = ?
Following the established pattern, we would expect the result to be 10 divided by 10, which equals 1. This intuitive understanding provides a compelling reason why 10<sup>0</sup> should equal 1. However, let's delve deeper into the mathematical reasoning behind this.
The Division Rule of Exponents
The division rule of exponents states that when dividing exponential expressions with the same base, you subtract the exponents:
- x<sup>m</sup> / x<sup>n</sup> = x<sup>(m-n)</sup>
Let's apply this rule to understand why 10<sup>0</sup> = 1:
Consider the expression 10<sup>n</sup> / 10<sup>n</sup>. Any number (except 0) divided by itself equals 1. Therefore:
- 10<sup>n</sup> / 10<sup>n</sup> = 1
Now, using the division rule of exponents:
- 10<sup>n</sup> / 10<sup>n</sup> = 10<sup>(n-n)</sup> = 10<sup>0</sup>
Since 10<sup>n</sup> / 10<sup>n</sup> equals both 1 and 10<sup>0</sup>, we can conclude:
- 10<sup>0</sup> = 1
This demonstrates that defining 10<sup>0</sup> as 1 is not arbitrary but a logical consequence of the established rules of exponents. It ensures that the rules of exponents remain consistent and universally applicable.
The Zero Exponent Rule: A Formal Definition
The zero exponent rule states that any non-zero number raised to the power of 0 is equal to 1. Mathematically:
- x<sup>0</sup> = 1, where x ≠ 0
This rule is a cornerstone of exponent manipulation and simplification. It's not just limited to the number 10; it applies to any number (excluding zero) that is raised to the power of zero. This rule maintains the consistency and coherence of mathematical operations involving exponents.
Why Not Zero? The Case of 0<sup>0</sup>
The expression 0<sup>0</sup> is a special case and is generally considered undefined in many contexts. This is because defining 0<sup>0</sup> as 1 would lead to inconsistencies in certain mathematical areas, particularly in calculus and combinatorics.
- Limit Considerations: In calculus, the limit of x<sup>y</sup> as both x and y approach 0 depends on the specific path taken. This means there isn't a unique value that can be assigned to 0<sup>0</sup> without creating contradictions.
- Combinatorial Arguments: In combinatorics, 0<sup>0</sup> is sometimes defined as 1, as it represents the number of ways to map a set of size 0 to a set of size 0. However, this is a specific convention and doesn't apply universally.
Therefore, to avoid ambiguity and maintain consistency, 0<sup>0</sup> is typically left undefined in most mathematical contexts.
Real-World Applications: Why This Matters
Understanding that 10<sup>0</sup> = 1, and more broadly, the zero exponent rule, isn't just an abstract mathematical concept. It has practical applications in various fields:
- Science: In scientific notation, large and small numbers are expressed as a number between 1 and 10 multiplied by a power of 10. For example, 1.23 x 10<sup>0</sup> is simply 1.23. Understanding the zero exponent is essential for accurate scientific calculations.
- Computer Science: In programming, exponents are used in algorithms and data structures. The zero exponent rule is crucial for simplifying expressions and optimizing code.
- Engineering: Engineers use exponents in various calculations, from determining the strength of materials to designing electrical circuits. Correctly applying the zero exponent rule ensures accurate results.
- Finance: Exponents are used in calculating compound interest and other financial metrics. Understanding the zero exponent can help in accurately assessing financial growth.
In these and many other fields, a solid grasp of exponents, including the zero exponent rule, is essential for problem-solving and decision-making.
Common Misconceptions
A common misconception is that any number to the power of zero is zero. This is incorrect. Only a number to the power of zero equals one, not is zero. Another misconception is thinking the rule only applies to 10, forgetting it's universal for all non-zero numbers. Remembering the division rule helps avoid this. Understanding these key principles prevents errors in calculations and mathematical reasoning.
Summarizing the Key Reasons: Why 10<sup>0</sup> = 1
Let's recap the reasons why 10<sup>0</sup> = 1:
- Pattern Continuation: Following the pattern of decreasing exponents of 10, dividing by 10 each time leads to 1.
- Division Rule of Exponents: Applying the rule x<sup>m</sup> / x<sup>n</sup> = x<sup>(m-n)</sup> proves that 10<sup>0</sup> = 1.
- Zero Exponent Rule: The general rule states that any non-zero number raised to the power of 0 is 1.
- Consistency: Defining 10<sup>0</sup> as 1 maintains consistency and coherence in mathematical operations involving exponents.
Understanding these reasons will help you remember and apply this important mathematical concept correctly.
Expanding the Concept: Negative Exponents
Now that we've solidified our understanding of the zero exponent, let's briefly touch on negative exponents, as they are closely related. A negative exponent indicates the reciprocal of the base raised to the positive exponent.
- Example: 10<sup>-1</sup> = 1 / 10<sup>1</sup> = 0.1
- 10<sup>-2</sup> = 1 / 10<sup>2</sup> = 0.01
- 10<sup>-3</sup> = 1 / 10<sup>3</sup> = 0.001
Notice that as the negative exponent increases in magnitude, the result becomes smaller. Negative exponents are used to represent very small numbers and are commonly used in scientific notation.
Examples and Practice Problems
To solidify your understanding, let's look at some examples and practice problems:
-
Example 1: Simplify 5<sup>0</sup> + 2<sup>3</sup>
- 5<sup>0</sup> = 1
- 2<sup>3</sup> = 2 * 2 * 2 = 8
- Therefore, 5<sup>0</sup> + 2<sup>3</sup> = 1 + 8 = 9
-
Example 2: Simplify (3<sup>2</sup> * 4<sup>0</sup>) / 6
- 3<sup>2</sup> = 3 * 3 = 9
- 4<sup>0</sup> = 1
- Therefore, (3<sup>2</sup> * 4<sup>0</sup>) / 6 = (9 * 1) / 6 = 9 / 6 = 1.5
-
Practice Problem 1: Simplify 7<sup>0</sup> - 3<sup>2</sup>
-
Practice Problem 2: Simplify (2<sup>4</sup> / 8) + 10<sup>0</sup>
By working through these examples and practice problems, you can strengthen your understanding of the zero exponent rule and its application in various mathematical expressions.
Conclusion: A Fundamental Truth
Understanding that 10 to the power of 0 (or any non-zero number to the power of 0) equals 1 is a fundamental concept in mathematics. It's not an arbitrary rule but a logical consequence of the established principles of exponents. This concept has wide-ranging applications in science, engineering, computer science, and other fields. By understanding the reasons behind this rule, you can avoid common misconceptions and apply it correctly in various mathematical contexts. Mastering this concept will strengthen your mathematical foundation and enable you to tackle more complex problems with confidence.
Latest Posts
Latest Posts
-
A Simcell With A Water Permeable Membrane
Nov 17, 2025
-
How To Divide A Bigger Number Into A Smaller Number
Nov 17, 2025
-
How To Solve Inequalities With Absolute Value
Nov 17, 2025
-
How Can You Tell Isotopes Apart
Nov 17, 2025
-
Which Subatomic Particle Determines The Identity Of The Atom
Nov 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 To The Power Of 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.