What Does B Represent In Y Mx B
pinupcasinoyukle
Nov 12, 2025 · 10 min read
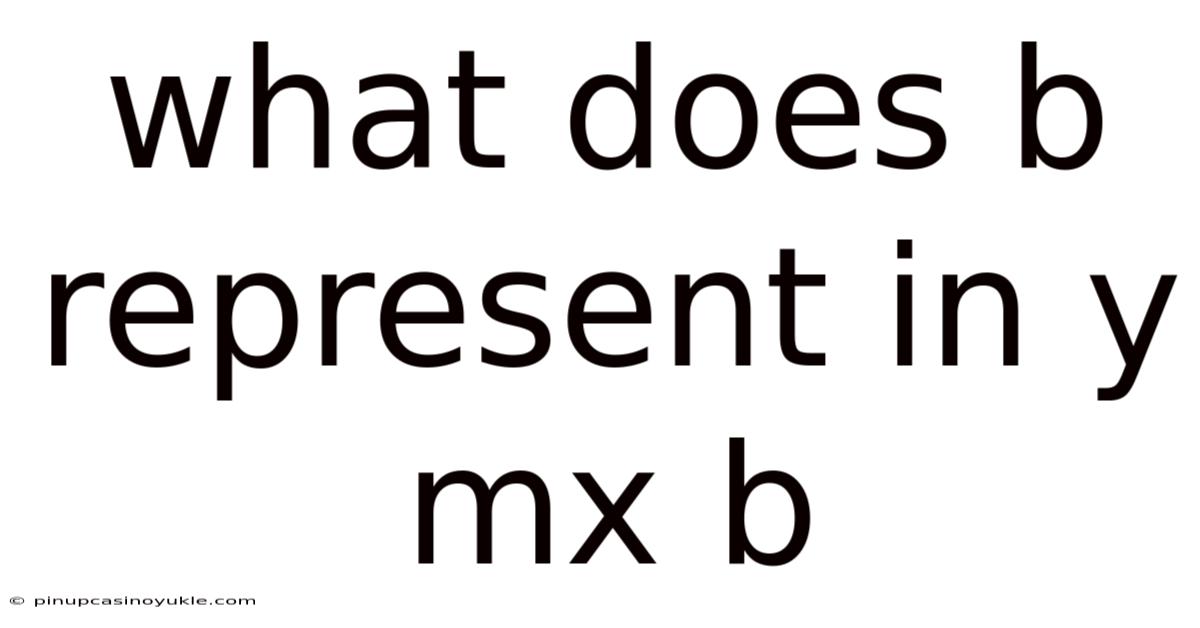
Table of Contents
The equation y = mx + b is a cornerstone of linear algebra, representing a straight line on a graph. While 'y' and 'x' denote the coordinates of any point on the line, and 'm' represents the slope, the term 'b' holds the key to understanding the line's vertical positioning. It signifies the y-intercept, the point where the line intersects the y-axis.
Unveiling the Y-Intercept: The Role of 'b' in y = mx + b
To fully grasp the meaning of 'b', we need to dissect the equation y = mx + b. This equation is known as the slope-intercept form of a linear equation. It elegantly presents the two essential pieces of information needed to define a straight line: its slope ('m') and its y-intercept ('b').
The slope (m) defines the line's steepness and direction. It indicates how much 'y' changes for every unit change in 'x'. A positive slope signifies an upward-sloping line, while a negative slope indicates a downward-sloping line. A slope of zero represents a horizontal line.
The y-intercept (b), on the other hand, pinpoints where the line crosses the vertical y-axis. At this point, the x-coordinate is always zero. Therefore, the y-intercept is the y-value when x = 0.
Understanding the Significance
-
Starting Point: 'b' essentially defines the "starting point" of the line on the y-axis. If you were to trace the line from left to right on a graph, 'b' would be the first point you encounter on the y-axis.
-
Vertical Shift: 'b' determines the vertical shift of the line. Changing the value of 'b' moves the entire line up or down along the y-axis, without altering its slope (steepness). Increasing 'b' shifts the line upwards, while decreasing 'b' shifts it downwards.
-
Unique Line Definition: For a given slope ('m'), different values of 'b' will generate different lines. All these lines will be parallel to each other (because they have the same slope), but each will have a unique y-intercept.
Deciphering y = mx + b with Examples
Let's solidify our understanding with a few concrete examples:
Example 1: y = 2x + 3
- Here, the slope (m) is 2. This means that for every 1 unit increase in 'x', 'y' increases by 2 units.
- The y-intercept (b) is 3. This indicates that the line crosses the y-axis at the point (0, 3).
Example 2: y = -x - 1
- The slope (m) is -1. This means that for every 1 unit increase in 'x', 'y' decreases by 1 unit. The line slopes downwards.
- The y-intercept (b) is -1. This signifies that the line intersects the y-axis at the point (0, -1).
Example 3: y = 0.5x + 0
- The slope (m) is 0.5. This means that for every 1 unit increase in 'x', 'y' increases by 0.5 units.
- The y-intercept (b) is 0. This means the line passes through the origin (0, 0). This equation can simply be written as y = 0.5x.
Example 4: y = 4
- This equation can be rewritten as y = 0x + 4. This is a horizontal line.
- The slope (m) is 0. This means that 'y' does not change regardless of the value of 'x'.
- The y-intercept (b) is 4. This signifies that the line intersects the y-axis at the point (0, 4).
Finding 'b' in Different Scenarios
Understanding how to find 'b' is crucial in various mathematical problems. Here are common scenarios and how to approach them:
-
Given the Slope and a Point: If you know the slope ('m') of a line and a point (x, y) that lies on the line, you can substitute these values into the equation y = mx + b and solve for 'b'.
-
For example, if the slope is 2 and the line passes through the point (1, 5), then:
- 5 = 2(1) + b
- 5 = 2 + b
- b = 3
Therefore, the y-intercept is 3, and the equation of the line is y = 2x + 3.
-
-
Given Two Points: If you know two points (x1, y1) and (x2, y2) that lie on the line, you can first calculate the slope ('m') using the formula:
- m = (y2 - y1) / (x2 - x1)
Once you have the slope, you can choose either of the two points and substitute the slope and the point's coordinates into the equation y = mx + b and solve for 'b', as demonstrated in the previous scenario.
-
For example, if the line passes through the points (1, 3) and (2, 5):
- m = (5 - 3) / (2 - 1) = 2 / 1 = 2
- Using the point (1, 3):
- 3 = 2(1) + b
- 3 = 2 + b
- b = 1
Therefore, the y-intercept is 1, and the equation of the line is y = 2x + 1.
-
From a Graph: If you have the graph of a line, simply look for the point where the line intersects the y-axis. The y-coordinate of that point is the value of 'b'.
Why is Understanding the Y-Intercept Important?
The y-intercept, represented by 'b' in the equation y = mx + b, is more than just a number; it's a fundamental concept with significant applications in various fields:
-
Mathematics: The y-intercept is crucial for defining a unique linear equation and understanding the relationship between variables in linear functions. It is essential for graphing lines, solving systems of equations, and analyzing linear relationships.
-
Science: In scientific experiments and data analysis, the y-intercept can represent the initial value of a variable or the baseline measurement. For instance, in a chemical reaction, the y-intercept might represent the initial concentration of a reactant.
-
Economics: In economics, the y-intercept can represent fixed costs, autonomous consumption, or other initial values in economic models. For example, in a cost function, the y-intercept represents the fixed costs that a company incurs regardless of its production level.
-
Engineering: In engineering applications, the y-intercept can represent initial conditions, offsets, or calibration points in systems. For instance, in a circuit analysis, the y-intercept might represent the initial voltage or current in a component.
-
Real-World Applications: Understanding the y-intercept is valuable in numerous real-world scenarios. For example, if you are tracking the growth of a plant over time, the y-intercept would represent the plant's initial height. If you are calculating the cost of a service based on a per-unit charge, the y-intercept might represent a fixed service fee.
Common Misconceptions about 'b'
- 'b' is always positive: The y-intercept ('b') can be positive, negative, or zero. A negative 'b' simply means the line intersects the y-axis below the x-axis.
- 'b' represents the x-intercept: The y-intercept is where the line crosses the y-axis, not the x-axis. The x-intercept is the point where the line crosses the x-axis, and it occurs when y = 0. To find the x-intercept, you set y = 0 in the equation y = mx + b and solve for x.
- 'b' is the starting point for all graphs: While 'b' is the starting point on the y-axis for a linear equation in slope-intercept form, this concept doesn't directly translate to all types of graphs. It's specifically relevant to understanding the position of a straight line.
- Ignoring 'b' is insignificant: Omitting or misinterpreting 'b' can lead to inaccurate representation and analysis of linear relationships. It is a crucial parameter that defines the precise location of the line on the graph.
Advanced Applications of y = mx + b
The fundamental concept of y = mx + b extends to more complex mathematical and real-world applications:
-
Systems of Linear Equations: The slope-intercept form is useful for solving systems of linear equations. By expressing equations in the form y = mx + b, you can easily compare the slopes and y-intercepts to determine whether the lines intersect, are parallel, or are coincident. This is essential in various fields like optimization and linear programming.
-
Linear Regression: In statistics, linear regression uses the equation y = mx + b (often with slightly different notation) to model the relationship between two variables. The 'm' represents the slope of the regression line, and the 'b' represents the y-intercept. Linear regression is used to predict values, identify trends, and analyze the strength and direction of linear relationships.
-
Calculus: The concept of the slope of a line (represented by 'm') forms the basis for the derivative in calculus. The derivative represents the instantaneous rate of change of a function at a specific point. While the equation y = mx + b describes a constant rate of change, the principles of slope and intercept are foundational to understanding more complex functions and their derivatives.
-
Computer Graphics: The equation y = mx + b is used extensively in computer graphics to draw lines, define shapes, and perform transformations. The slope and y-intercept are key parameters for rendering lines and objects on a screen.
Tips and Tricks for Mastering y = mx + b
-
Practice Regularly: The best way to master the concept of y = mx + b is to practice solving problems involving finding the slope, y-intercept, and equation of a line. Work through a variety of examples with different scenarios and values.
-
Visualize with Graphs: Use graphing tools or software to visualize the lines represented by different equations. This will help you develop a strong intuition for how the slope and y-intercept affect the line's position and orientation.
-
Relate to Real-World Examples: Look for real-world examples of linear relationships to solidify your understanding. For instance, consider the relationship between the number of hours worked and the amount of money earned, or the relationship between the distance traveled and the time taken at a constant speed.
-
Break Down Complex Problems: When faced with complex problems involving linear equations, break them down into smaller, more manageable steps. Identify the knowns and unknowns, and use the equation y = mx + b to solve for the desired variables.
-
Use Online Resources: There are numerous online resources, including tutorials, videos, and interactive exercises, that can help you learn and practice the concepts related to y = mx + b. Take advantage of these resources to enhance your understanding.
The Broader Context of Linear Equations
While the equation y = mx + b is a fundamental building block, it's important to remember that it represents just one type of linear equation. Linear equations can also be expressed in other forms, such as:
- Standard Form: Ax + By = C, where A, B, and C are constants.
- Point-Slope Form: y - y1 = m(x - x1), where (x1, y1) is a point on the line and m is the slope.
Each form has its advantages and disadvantages, depending on the specific application. Understanding the relationships between these different forms can enhance your problem-solving skills. Furthermore, the concepts of linear equations extend into higher dimensions and are fundamental to linear algebra, a branch of mathematics with vast applications in science, engineering, and computer science.
Conclusion: 'b' as the Anchor of the Line
In the realm of linear equations, the equation y = mx + b stands as a powerful tool. The variable 'b', representing the y-intercept, provides the crucial vertical anchor for the line, complementing the slope 'm' which dictates its direction. Understanding 'b' is not merely about memorizing a formula; it's about grasping a fundamental concept that unlocks a deeper understanding of linear relationships and their applications across various disciplines. By mastering the significance of 'b', you empower yourself to analyze, interpret, and manipulate linear equations with confidence and precision. From graphing lines to solving complex problems in science and engineering, the y-intercept serves as a key to unlocking the power of linear mathematics.
Latest Posts
Latest Posts
-
What Determines The Carrying Capacity Of A Population
Nov 12, 2025
-
How To Find The Atomic Weight
Nov 12, 2025
-
Factoring The Difference Of Two Perfect Squares
Nov 12, 2025
-
What Are Examples Of Elastic Potential Energy
Nov 12, 2025
-
What Is Factor Pairs In Math
Nov 12, 2025
Related Post
Thank you for visiting our website which covers about What Does B Represent In Y Mx B . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.