Slope Is Change In Y Over X
pinupcasinoyukle
Nov 28, 2025 · 11 min read
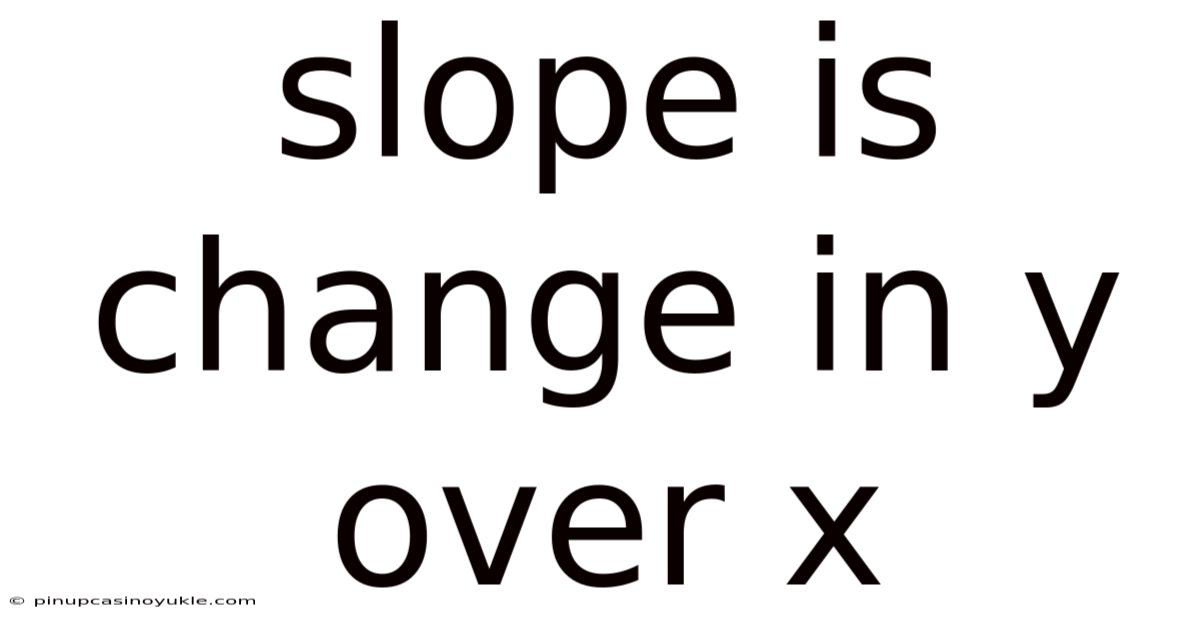
Table of Contents
In mathematics, particularly in coordinate geometry, slope is a fundamental concept that describes both the direction and steepness of a line. Defined as the "change in y over x," the slope provides a quantitative measure of how much the y-value changes for a given change in the x-value. This seemingly simple ratio is the key to understanding linear relationships, predicting future trends, and solving a variety of real-world problems.
Understanding Slope: The Basics
The slope of a line, often denoted by the letter m, quantifies the rate at which the line rises or falls as you move along the x-axis. It answers the question: "For every unit increase in x, how much does y change?" A positive slope indicates an increasing line, where y increases as x increases. Conversely, a negative slope indicates a decreasing line, where y decreases as x increases. A slope of zero represents a horizontal line, indicating no change in y as x changes. An undefined slope, on the other hand, signifies a vertical line, where there is an infinite change in y for a zero change in x.
The Formula: Change in Y over Change in X
The slope formula, derived from the concept of "rise over run," is expressed as:
m = (y₂ - y₁) / (x₂ - x₁)
where:
- m represents the slope
- (x₁, y₁) and (x₂, y₂) are two distinct points on the line
This formula essentially calculates the difference in y-coordinates (the "rise") divided by the difference in x-coordinates (the "run") between two points on the line. The order of subtraction must be consistent for both the y and x values.
Visualizing Slope
Understanding slope is greatly enhanced by visualizing it on a coordinate plane. Consider a line passing through two points, A(1, 2) and B(4, 6). To find the slope, we can apply the formula:
m = (6 - 2) / (4 - 1) = 4 / 3
This means that for every 3 units you move to the right along the x-axis, the line rises 4 units along the y-axis. Graphically, you can see this "rise over run" as a series of steps along the line.
Different Types of Slopes
Understanding the different types of slopes is crucial for interpreting linear relationships:
- Positive Slope: The line rises from left to right. A larger positive slope indicates a steeper incline.
- Negative Slope: The line falls from left to right. A larger negative slope (in absolute value) indicates a steeper decline.
- Zero Slope: The line is horizontal. This indicates a constant y-value, regardless of the x-value.
- Undefined Slope: The line is vertical. This indicates a constant x-value, regardless of the y-value. This occurs when the denominator in the slope formula is zero, leading to division by zero.
Calculating Slope: Step-by-Step Guide
Calculating the slope of a line is a straightforward process using the slope formula. Here's a detailed guide:
Step 1: Identify Two Points on the Line
The first step is to identify two distinct points on the line. These points can be given directly as coordinates (x₁, y₁) and (x₂, y₂), or they can be determined from a graph. Accuracy in identifying these points is crucial for obtaining the correct slope.
Step 2: Label the Coordinates
Once you have identified the two points, label their coordinates as (x₁, y₁) and (x₂, y₂). It doesn't matter which point you label as (x₁, y₁) and which you label as (x₂, y₂), as long as you are consistent in the next step.
Step 3: Apply the Slope Formula
Substitute the coordinates you identified in Step 2 into the slope formula:
m = (y₂ - y₁) / (x₂ - x₁)
Step 4: Simplify the Expression
Perform the subtraction in both the numerator and the denominator, and then simplify the resulting fraction. The simplified fraction represents the slope of the line.
Example 1: Finding the Slope Given Two Points
Let's say we have two points: A(2, 3) and B(5, 7).
- x₁ = 2, y₁ = 3
- x₂ = 5, y₂ = 7
Applying the formula:
m = (7 - 3) / (5 - 2) = 4 / 3
Therefore, the slope of the line passing through points A and B is 4/3.
Example 2: Finding the Slope from a Graph
Imagine a line on a graph passing through the points (1, -1) and (3, 5).
- x₁ = 1, y₁ = -1
- x₂ = 3, y₂ = 5
Applying the formula:
m = (5 - (-1)) / (3 - 1) = 6 / 2 = 3
Therefore, the slope of the line is 3.
Example 3: Dealing with Negative Values
Consider the points (-2, 4) and (1, -2).
- x₁ = -2, y₁ = 4
- x₂ = 1, y₂ = -2
Applying the formula:
m = (-2 - 4) / (1 - (-2)) = -6 / 3 = -2
Therefore, the slope of the line is -2. This indicates a decreasing line.
Common Mistakes to Avoid
- Inconsistent Order: Ensure that you subtract the y-coordinates and x-coordinates in the same order. For example, if you use (y₂ - y₁) in the numerator, you must use (x₂ - x₁) in the denominator.
- Incorrect Substitution: Double-check that you are substituting the correct values for x₁ , y₁, x₂, and y₂ into the formula.
- Sign Errors: Pay close attention to negative signs when substituting values into the formula and when simplifying the expression.
- Division by Zero: Be aware that if the denominator (x₂ - x₁) is zero, the slope is undefined. This occurs for vertical lines.
The Significance of Slope: Real-World Applications
The concept of slope is not just a theoretical mathematical idea; it has numerous practical applications in various fields:
- Architecture and Engineering: Slope is crucial in designing roads, bridges, and buildings. Civil engineers use slope to determine the grade of a road, ensuring proper drainage and safe driving conditions. Architects consider slope when designing ramps for accessibility and roofs for water runoff.
- Economics: Economists use slope to analyze supply and demand curves. The slope of a supply curve indicates how much the quantity supplied changes in response to a change in price. Similarly, the slope of a demand curve indicates how much the quantity demanded changes in response to a change in price.
- Physics: In physics, slope is used to represent velocity, acceleration, and other rates of change. For example, the slope of a position-time graph represents the velocity of an object. The slope of a velocity-time graph represents the acceleration of an object.
- Finance: Financial analysts use slope to analyze trends in stock prices and other financial data. The slope of a trend line can indicate the rate at which a stock price is increasing or decreasing.
- Geography: Geographers use slope to analyze the steepness of terrain. Slope is an important factor in determining the suitability of land for agriculture, construction, and other purposes.
- Computer Graphics: Slope is used in computer graphics to draw lines and curves. The slope of a line determines its direction and steepness, which are essential for creating realistic images.
- Machine Learning: In machine learning, slope is a key component of linear regression models. The slope of the regression line represents the relationship between the independent and dependent variables.
Examples in Detail
- Road Grade: A road with a grade of 6% has a slope of 0.06. This means that for every 100 feet of horizontal distance, the road rises 6 feet.
- Stock Price Trend: If a stock price increases by $5 per month, the slope of the trend line is 5. This indicates a positive trend.
- Velocity: If a car travels 100 miles in 2 hours, its average velocity is 50 miles per hour. This is the slope of the distance-time graph.
Slope-Intercept Form: A Powerful Equation
The slope-intercept form is a specific form of a linear equation that highlights the slope and y-intercept of a line. This form is expressed as:
y = mx + b
where:
- y is the dependent variable
- x is the independent variable
- m is the slope of the line
- b is the y-intercept (the point where the line crosses the y-axis)
Advantages of Slope-Intercept Form
- Easy Identification of Slope and Y-intercept: The slope-intercept form directly reveals the slope and y-intercept of a line, making it easy to visualize and understand the line's characteristics.
- Graphing Lines: This form simplifies the process of graphing a line. You can plot the y-intercept (0, b) and then use the slope m to find another point on the line. For example, if the slope is 2/3, you can move 3 units to the right from the y-intercept and then 2 units up to find another point.
- Writing Equations of Lines: If you know the slope and y-intercept of a line, you can easily write its equation in slope-intercept form.
Converting to Slope-Intercept Form
To convert a linear equation into slope-intercept form, you need to isolate y on one side of the equation. This usually involves rearranging the terms and performing algebraic operations.
Example:
Convert the equation 2x + 3y = 6 into slope-intercept form.
-
Subtract 2x from both sides:
3y = -2x + 6 -
Divide both sides by 3:
y = (-2/3)x + 2
Now the equation is in slope-intercept form, where the slope m is -2/3 and the y-intercept b is 2.
Slope and Parallel & Perpendicular Lines
The concept of slope is fundamental in determining the relationship between two lines, specifically whether they are parallel or perpendicular.
Parallel Lines
Parallel lines are lines that lie in the same plane and never intersect. A key characteristic of parallel lines is that they have the same slope. If two lines have the same slope, they are either parallel or the same line (if they also have the same y-intercept).
Example:
The lines y = 2x + 3 and y = 2x - 1 are parallel because they both have a slope of 2.
Perpendicular Lines
Perpendicular lines are lines that intersect at a right angle (90 degrees). The slopes of perpendicular lines have a special relationship: they are negative reciprocals of each other. This means that if one line has a slope of m, the slope of a perpendicular line is -1/m.
Example:
The lines y = 2x + 3 and y = (-1/2)x + 1 are perpendicular because their slopes are 2 and -1/2, respectively. The product of their slopes is 2 * (-1/2) = -1, which is a characteristic of perpendicular lines.
Determining Parallelism and Perpendicularity
To determine whether two lines are parallel or perpendicular, follow these steps:
- Find the Slopes: Determine the slopes of both lines. If the equations are not in slope-intercept form, convert them first.
- Compare the Slopes:
- If the slopes are equal, the lines are parallel (or the same line).
- If the slopes are negative reciprocals of each other, the lines are perpendicular.
- If neither of these conditions is met, the lines are neither parallel nor perpendicular.
Advanced Concepts Related to Slope
While the basic concept of slope is relatively straightforward, it extends into more advanced areas of mathematics and beyond.
Calculus: Derivatives and Tangent Lines
In calculus, the derivative of a function at a point represents the slope of the tangent line to the function's graph at that point. The tangent line is a line that touches the curve at a single point and has the same direction as the curve at that point. This connection between slope and derivatives is fundamental to understanding rates of change and optimization problems.
Linear Approximations
The concept of slope is used in linear approximations to estimate the value of a function near a known point. By using the tangent line at a known point, we can approximate the function's value at nearby points. This is particularly useful when dealing with complex functions where direct calculation is difficult.
Vectors and Direction
In linear algebra, vectors have both magnitude and direction. The slope of a line can be related to the direction vector of the line. The direction vector provides information about the orientation of the line in space.
Surfaces in Three Dimensions
The concept of slope extends to surfaces in three dimensions, where it is represented by the gradient vector. The gradient vector points in the direction of the steepest ascent on the surface and its magnitude represents the rate of change in that direction.
Applications in Optimization
Slope is used in optimization algorithms to find the maximum or minimum value of a function. By analyzing the slope of the function, algorithms can determine the direction to move in order to reach the optimal value.
Conclusion
The concept of "slope is change in y over x" is a cornerstone of mathematics, providing a fundamental way to understand and quantify linear relationships. From calculating the steepness of a road to analyzing economic trends, slope plays a crucial role in various fields. By mastering the slope formula, understanding different types of slopes, and recognizing its applications, you can gain a deeper appreciation for the power and versatility of this essential mathematical concept. The slope-intercept form further enhances this understanding by providing a direct link between the equation of a line and its visual representation. Moreover, the relationship between slope and parallel/perpendicular lines adds another layer of insight into the geometry of lines. As you continue your mathematical journey, the principles of slope will undoubtedly serve as a valuable tool for problem-solving and critical thinking.
Latest Posts
Latest Posts
-
Multi Step Word Problems For 4th Graders
Nov 28, 2025
-
Whats The Associative Property Of Addition
Nov 28, 2025
-
Difference Between Dot Product And Cross Product Of Vectors
Nov 28, 2025
-
Use Implicit Differentiation To Find Dy Dx
Nov 28, 2025
-
How Do I Solve 2 Step Equations
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about Slope Is Change In Y Over X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.