Negative Number Plus A Negative Number Equals
pinupcasinoyukle
Nov 12, 2025 · 7 min read
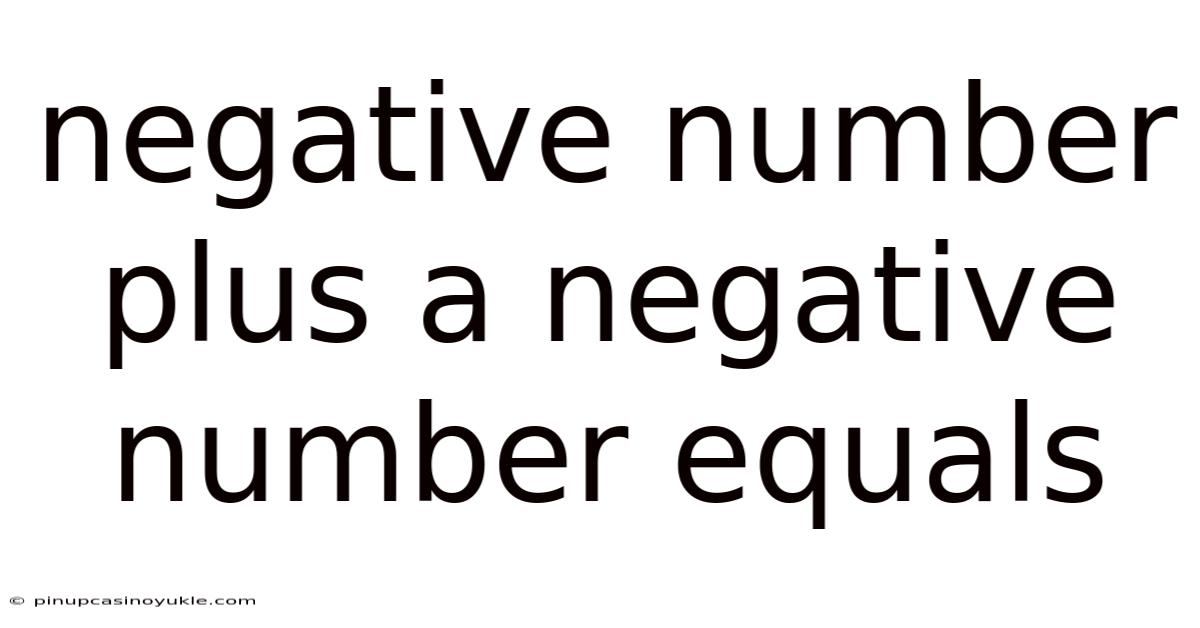
Table of Contents
The dance of numbers extends beyond the realm of positives, venturing into the intriguing territory of negative numbers. One fundamental operation within this domain involves the addition of negative numbers. Understanding the mechanics of this operation is crucial for mastering basic arithmetic and its applications in various fields.
Defining Negative Numbers
Negative numbers represent values less than zero. They are commonly used to denote deficits, debts, temperatures below zero, or positions on a number line to the left of zero. A negative number is always preceded by a minus sign (-). For example, -5 represents a value that is five units less than zero.
Understanding Addition
Addition, in its simplest form, is the process of combining two or more numbers to find their total or sum. When dealing with positive numbers, addition is straightforward: 2 + 3 = 5. However, the concept of addition takes on a nuanced meaning when negative numbers are involved.
Adding a Negative Number to a Negative Number
When adding a negative number to another negative number, the result is always a negative number. This can be understood through several analogies and mathematical explanations:
1. The Number Line
The number line provides a visual representation of numbers and their relationships. Zero sits at the center, with positive numbers extending to the right and negative numbers extending to the left.
To add two negative numbers on the number line, start at zero and move to the left by the absolute value of the first negative number. Then, from that point, move further to the left by the absolute value of the second negative number. The final position on the number line represents the sum of the two negative numbers.
-
Example: -3 + (-2)
- Start at zero.
- Move 3 units to the left to reach -3.
- From -3, move 2 units further to the left.
- You end up at -5.
Therefore, -3 + (-2) = -5.
2. Analogy: Debt and Owed Money
Imagine you owe $5 to a friend (represented as -5). Then, you borrow an additional $3 (represented as -3) from the same friend. Your total debt is now $8, which can be represented as -8.
In mathematical terms: -5 + (-3) = -8.
This analogy illustrates that adding two debts (negative numbers) results in an even larger debt (a more negative number).
3. The Rule of Signs
A general rule for adding numbers with the same sign is to add their absolute values and keep the common sign. In the case of two negative numbers:
- Find the absolute value of each number. The absolute value of a number is its distance from zero, regardless of its sign. For example, |-5| = 5 and |-3| = 3.
- Add the absolute values together. In the example, 5 + 3 = 8.
- Since both numbers are negative, the sum is also negative. Therefore, the result is -8.
4. Mathematical Explanation
Consider two negative numbers, -a and -b, where a and b are positive numbers. The addition of -a and -b can be expressed as:
-a + (-b) = -(a + b)
This shows that you add the magnitudes a and b and then apply the negative sign to the result.
-
Example: -7 + (-4)
- a = 7, b = 4
- a + b = 7 + 4 = 11
- -(a + b) = -11
Therefore, -7 + (-4) = -11.
Examples of Adding Negative Numbers
Here are more examples to solidify the concept:
-
-10 + (-5) = -15
- Imagine you are 10 steps behind your goal, and then you take another 5 steps backward. You are now 15 steps behind your goal.
-
-25 + (-15) = -40
- If a stock loses 25 points one day and then loses another 15 points the next day, the total loss is 40 points.
-
-1 + (-1) = -2
- This is a simple case showing that adding two negative ones results in negative two.
-
-100 + (-200) = -300
- If a company has a debt of $100 and incurs an additional debt of $200, the total debt is $300.
-
-0.5 + (-0.5) = -1
- This shows that even with decimal numbers, the same principle applies.
-
-1/2 + (-1/2) = -1
- Adding two halves together results in a whole, and since both are negative, the result is negative one.
-
-π + (-π) = -2π
- Even with irrational numbers, the rule holds. Adding two negative πs results in negative two πs.
Common Mistakes to Avoid
- Confusing Addition with Multiplication:
- A common mistake is to apply the rules of multiplication to addition. Remember, when multiplying two negative numbers, the result is positive. However, when adding two negative numbers, the result is always negative.
- Example:
- -2 + (-3) = -5 (Addition)
- -2 * (-3) = 6 (Multiplication)
- Forgetting the Negative Sign:
- Always remember that the sum of two negative numbers is negative. Ensure that the negative sign is included in the final answer.
- Incorrectly Applying the Absolute Value:
- While absolute values are used to find the magnitude of the numbers, the sign of the result depends on the operation being performed. In addition, the sign remains negative.
Applications in Real Life
The addition of negative numbers is not just an abstract mathematical concept; it has practical applications in various real-life scenarios:
- Finance:
- Calculating debt: If you have multiple debts, adding them together (as negative numbers) gives you your total debt.
- Budgeting: Tracking expenses (negative numbers) against income (positive numbers) to determine cash flow.
- Temperature:
- Determining temperature changes: If the temperature drops by a certain amount and then drops again, adding the negative changes gives you the total temperature drop.
- Sports:
- Goal difference: In sports like soccer, goal difference is calculated by subtracting the number of goals conceded from the number of goals scored. Negative numbers can indicate a team's performance relative to their opponents.
- Science and Engineering:
- Calculating voltage drops: In electrical circuits, voltage drops can be represented as negative numbers. Adding these drops helps determine the total voltage in a circuit.
- Altitude and Depth: Measuring changes in elevation below sea level.
Advanced Concepts and Extensions
- Adding Multiple Negative Numbers:
- The same principle applies when adding more than two negative numbers. Add their absolute values and keep the negative sign.
- Example: -2 + (-5) + (-1) + (-3) = -(2 + 5 + 1 + 3) = -11
- Combining Positive and Negative Numbers:
- When adding positive and negative numbers, subtract the smaller absolute value from the larger absolute value. The sign of the result is the same as the sign of the number with the larger absolute value.
- Example: -7 + 5 = -2 (since |-7| > |5| and -7 is negative)
- Example: 7 + (-5) = 2 (since |7| > |-5| and 7 is positive)
- Algebraic Expressions:
- The concept of adding negative numbers extends to algebraic expressions. Simplify expressions by combining like terms, including negative terms.
- Example: 3x - 2x - 5x = (3 - 2 - 5)x = -4x
- Complex Numbers:
- In complex numbers, which have a real and imaginary part, negative numbers can be part of either component.
- Example: (2 - 3i) + (-1 - i) = (2 + (-1)) + (-3i + (-i)) = 1 - 4i
The Role of Negative Numbers in Mathematics
Negative numbers are fundamental in mathematics for several reasons:
- Completing Operations:
- Negative numbers allow subtraction to be performed universally. Without negative numbers, subtraction would be limited to cases where the number being subtracted is smaller than the original number.
- Solving Equations:
- Negative numbers are essential for solving algebraic equations. They allow for solutions that are less than zero.
- Graphing and Coordinate Systems:
- Negative numbers are necessary for graphing functions and representing points in coordinate systems. They extend the number line into two dimensions, allowing for the representation of a wide range of mathematical relationships.
- Calculus and Analysis:
- In calculus, negative numbers are used to represent rates of change, areas below the x-axis, and other important concepts.
Conclusion
Adding negative numbers together might seem counterintuitive at first, but it follows consistent mathematical rules. By understanding the concept through number lines, real-world analogies, and simple rules, you can master this fundamental operation. The sum of two negative numbers is always a negative number, and this principle applies across various fields, from finance to science. Embracing negative numbers expands your understanding of mathematics and its practical applications in the world around you.
Latest Posts
Latest Posts
-
Ficks Law Of Diffusion Transcellular Pathway
Nov 12, 2025
-
What Separates The Inner And Outer Planets
Nov 12, 2025
-
What Is The Difference Between Cytoplasm And Cytosol
Nov 12, 2025
-
Major And Minor Grooves In Dna
Nov 12, 2025
-
Solution That Binds To Proteins To Make Them Uniformly Negative
Nov 12, 2025
Related Post
Thank you for visiting our website which covers about Negative Number Plus A Negative Number Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.