Negative Divided By A Positive Equals
pinupcasinoyukle
Nov 09, 2025 · 7 min read
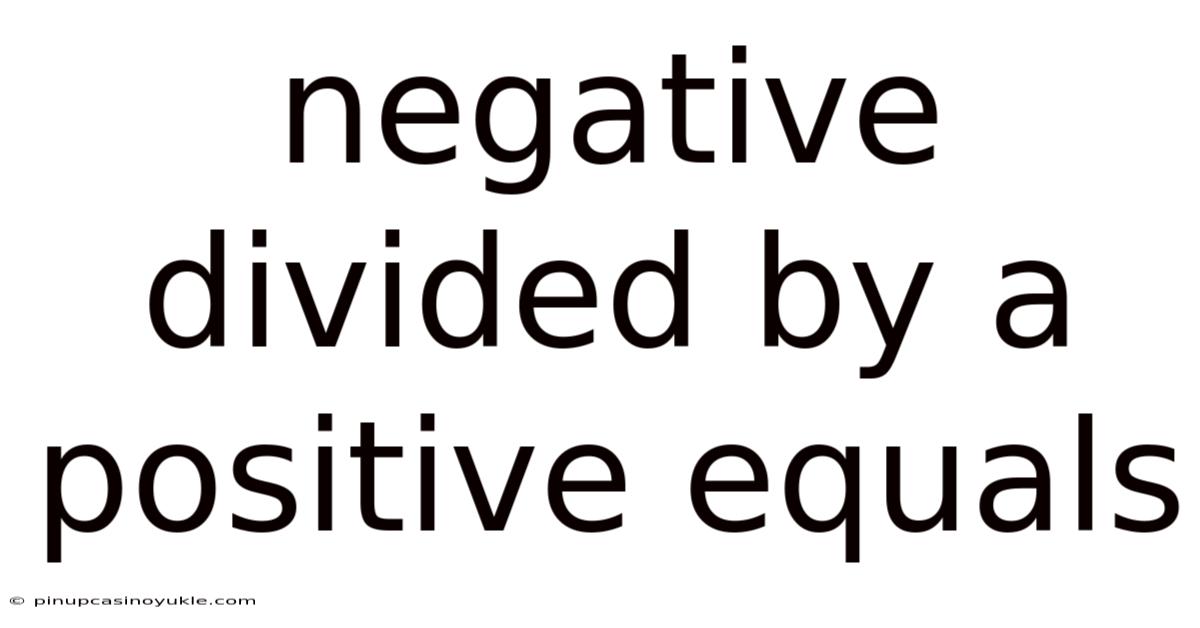
Table of Contents
Dividing a negative number by a positive number is a fundamental operation in arithmetic that extends beyond simple counting and delves into the world of signed numbers. This operation, governed by specific rules, plays a crucial role in various mathematical fields, from basic algebra to advanced calculus. Understanding the underlying principles of this operation is essential for anyone seeking a solid foundation in mathematics.
The Basic Rule: Negative Divided by Positive Equals Negative
The core concept can be encapsulated in a simple rule: when you divide a negative number by a positive number, the result is always a negative number. This rule stems from the properties of signed numbers and how they interact within the context of division.
Mathematically, this can be represented as:
(-a) / b = - (a / b)
Where:
ais any positive numberbis any positive number
This formula illustrates that the negative sign can be factored out, making it clear that the result will be the negative of the quotient of a and b.
Understanding the "Why": Conceptual Explanations
While the rule is straightforward, understanding the "why" behind it provides a deeper, more intuitive grasp of the concept. Several approaches can help illuminate the reasoning:
1. Division as the Inverse of Multiplication
Division is the inverse operation of multiplication. To understand why a negative divided by a positive results in a negative, consider the multiplication rule: a negative number multiplied by a negative number results in a positive number, while a negative number multiplied by a positive number results in a negative number.
For example, let's say we want to solve:
(-6) / 2 = ?
This is equivalent to asking:
2 * ? = -6
To satisfy this equation, the missing number must be -3 because 2 * (-3) = -6. This directly illustrates that a negative number (-6) divided by a positive number (2) results in a negative number (-3).
2. The Number Line Approach
Visualizing numbers on a number line can also provide a clear understanding. Consider the number line with zero at the center, positive numbers extending to the right, and negative numbers extending to the left.
When you divide a positive number by a positive number, you're essentially splitting a quantity into equal positive parts. For example, 6 / 2 means splitting 6 into 2 equal parts, each of which is 3 (moving from 0 to 6, then dividing that distance into two equal segments).
Now, consider dividing a negative number by a positive number, such as (-6) / 2. This can be interpreted as splitting a negative quantity (-6) into 2 equal parts. Starting at 0 and moving to -6, dividing that distance into two equal segments results in each segment reaching -3. This visually demonstrates that the result is a negative number.
3. Distributive Property Analogy
The distributive property can also offer an intuitive explanation. Although it's not a direct application, the principle of distribution helps to understand how signs behave.
Consider the expression:
b * (x + y) = bx + by
If we want to achieve a negative result on the right side (bx + by), and b is positive, then either x or y (or both) must be negative. In the context of division, this translates to the idea that if the product (dividend) is negative and one factor (divisor) is positive, the other factor (quotient) must be negative.
Step-by-Step Examples
To solidify understanding, let's work through several examples:
Example 1:
(-10) / 5 = ?
- Identify the signs: We have a negative number (-10) being divided by a positive number (5).
- Apply the rule: A negative divided by a positive results in a negative.
- Perform the division: 10 / 5 = 2
- Apply the negative sign: The final answer is -2.
Example 2:
(-25) / 4 = ?
- Identify the signs: We have a negative number (-25) being divided by a positive number (4).
- Apply the rule: A negative divided by a positive results in a negative.
- Perform the division: 25 / 4 = 6.25
- Apply the negative sign: The final answer is -6.25.
Example 3:
(-1) / 100 = ?
- Identify the signs: We have a negative number (-1) being divided by a positive number (100).
- Apply the rule: A negative divided by a positive results in a negative.
- Perform the division: 1 / 100 = 0.01
- Apply the negative sign: The final answer is -0.01.
Common Mistakes to Avoid
While the rule itself is simple, there are common mistakes students often make:
- Forgetting the negative sign: This is the most common error. Always remember to apply the negative sign to the result after performing the division.
- Confusing it with multiplication rules: While related, the rules for multiplication and division of signed numbers are distinct. Remember:
- Negative * Negative = Positive
- Negative * Positive = Negative
- Negative / Positive = Negative
- Negative / Negative = Positive
- Incorrectly applying order of operations: Ensure that division is performed in the correct order according to the order of operations (PEMDAS/BODMAS).
Practical Applications
Understanding this rule is not just an academic exercise; it has practical applications in various real-world scenarios:
- Finance: Calculating losses. If a company loses $10,000 over 5 months, the average monthly loss is (-$10,000) / 5 = -$2,000.
- Temperature: Calculating average temperature drops. If the temperature drops 15 degrees over 3 hours, the average hourly drop is (-15) / 3 = -5 degrees per hour.
- Physics: Calculating deceleration. If an object slows down from 20 m/s to 0 m/s over 4 seconds, the acceleration is (-20) / 4 = -5 m/s², where the negative sign indicates deceleration.
- Data Analysis: Calculating percentage decreases.
Negative Divided by a Negative
While this article focuses on a negative divided by a positive, it's important to briefly touch upon the opposite: a negative divided by a negative. In this case, the rule is:
Negative divided by Negative = Positive
Mathematically:
(-a) / (-b) = a / b
The reasoning is similar to the multiplication rule: a negative times a negative equals a positive. Therefore, the inverse operation (division) follows the same principle.
For example:
(-10) / (-2) = 5
Advanced Applications and Considerations
In more advanced mathematical contexts, the concept of dividing a negative number by a positive number remains fundamental, but its application can become more nuanced.
1. Complex Numbers
While complex numbers introduce imaginary units, the underlying principles of signed arithmetic still apply. When dealing with complex numbers, division can involve multiplying by the conjugate to eliminate the imaginary part in the denominator, but the sign rules remain consistent.
2. Calculus
In calculus, derivatives and integrals often involve negative numbers. For instance, the derivative of a decreasing function is negative. When calculating rates of change, you might encounter scenarios where a negative change in a quantity is divided by a positive change in time, resulting in a negative rate of change.
3. Linear Algebra
Linear algebra deals with vectors and matrices, and these can contain negative values. Operations like matrix inversion and solving systems of linear equations can involve dividing negative numbers by positive numbers, requiring careful attention to signs.
4. Statistics
In statistics, calculating deviations from the mean often involves negative numbers. When computing standard deviations or other statistical measures, dividing negative values by positive sample sizes is a common operation.
FAQ
-
Why is it important to understand this rule?
Understanding this rule is crucial for building a strong foundation in arithmetic and algebra. It's essential for solving equations, understanding rates of change, and interpreting data in various fields.
-
What happens if I divide zero by a positive number?
Zero divided by any non-zero number (positive or negative) is always zero. 0 / a = 0 (where a ≠ 0).
-
Can I divide a positive number by a negative number?
Yes, you can. The result is negative, following the same principle as dividing a negative number by a positive number. a / (-b) = -(a / b).
-
Does this rule apply to fractions and decimals?
Yes, the rule applies to all real numbers, including fractions and decimals. For example, (-1/2) / (1/4) = -2.
Conclusion
Dividing a negative number by a positive number is a foundational concept in mathematics. The rule, that the result is always negative, is derived from the fundamental properties of signed numbers and their behavior under division. This understanding is vital not only for academic pursuits but also for practical applications in finance, science, and data analysis. By grasping the underlying principles, practicing with examples, and avoiding common mistakes, you can confidently navigate mathematical problems involving signed numbers and build a stronger mathematical skillset. The key is to remember the core rule and to understand the relationship between division and multiplication, allowing for a more intuitive grasp of the concept.
Latest Posts
Latest Posts
-
If Banks Cannot Lend All Of Their Excess Reserves
Nov 09, 2025
-
Given The Piecewise Function Above Evaluate The Following Statements
Nov 09, 2025
-
Whats The Difference Between Endothermic And Exothermic Reactions
Nov 09, 2025
-
Chain Rule Quotient Rule And Product Rule
Nov 09, 2025
-
Top Down And Bottom Up Processing Psychology
Nov 09, 2025
Related Post
Thank you for visiting our website which covers about Negative Divided By A Positive Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.