Any Number Multiplied By 1 Is The Number Itself
pinupcasinoyukle
Nov 18, 2025 · 10 min read
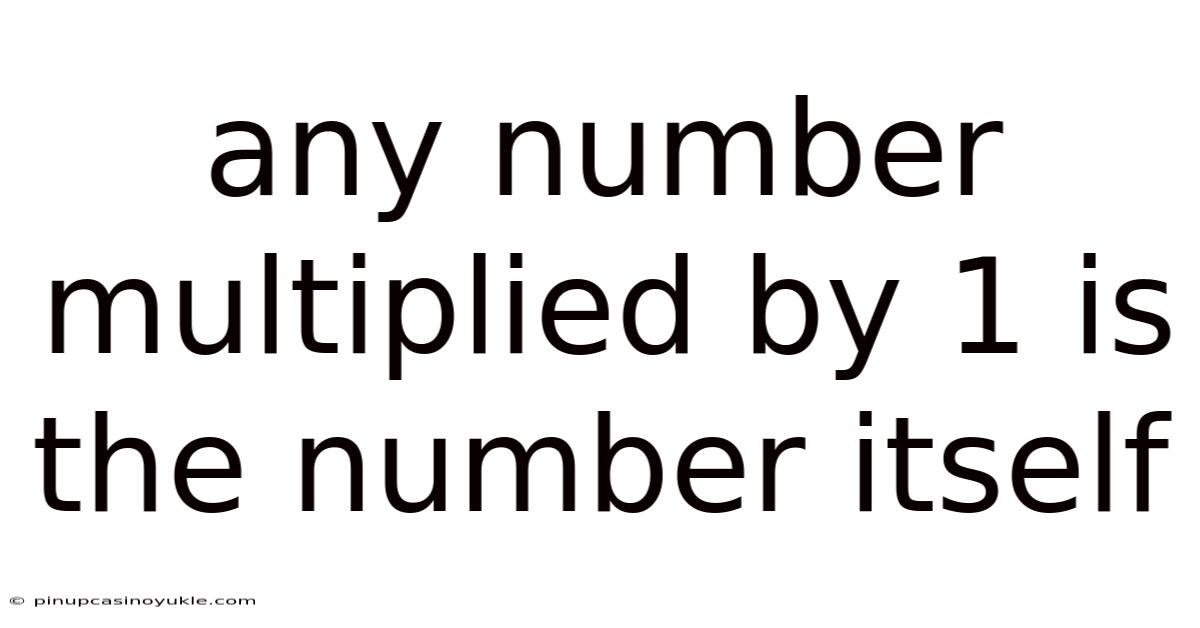
Table of Contents
Any number, whether it's a whole number, a fraction, a decimal, or even a complex number, remains unchanged when multiplied by one. This fundamental principle, known as the identity property of multiplication, is a cornerstone of arithmetic and algebra.
Understanding the Identity Property of Multiplication
The identity property of multiplication states that for any number a, a x 1 = a and 1 x a = a. In simpler terms, multiplying any number by 1 doesn't alter its value. The number '1' is therefore referred to as the multiplicative identity.
This concept is intuitive and easy to grasp with whole numbers. For example, 5 x 1 = 5, 123 x 1 = 123. However, its significance extends far beyond simple arithmetic, playing a crucial role in algebraic manipulations, simplifying equations, and understanding more advanced mathematical concepts.
A Deeper Dive: Why Does This Happen?
To understand why the identity property of multiplication works, it's helpful to consider the fundamental meaning of multiplication. Multiplication can be thought of as repeated addition. For example, 3 x 4 means adding the number 3 to itself four times (3 + 3 + 3 + 3 = 12).
Now, let's apply this understanding to multiplication by 1. When we multiply a number by 1, we're essentially adding that number to itself once. Or rather, we are taking one 'set' of that number. Therefore, the result is simply the original number itself. For example, 7 x 1 means taking one set of 7, which is just 7.
Another way to visualize this is to think of multiplication as scaling. Multiplying by a number greater than 1 increases the size of the original number. Multiplying by a number between 0 and 1 decreases the size of the original number. Multiplying by 1 leaves the size unchanged, preserving the original quantity.
The Identity Property in Action: Examples Across Number Systems
The beauty of the identity property of multiplication lies in its universality. It applies to all types of numbers, not just whole numbers. Let's explore some examples:
-
Whole Numbers: As mentioned earlier, this is the most straightforward application. Examples include:
- 0 x 1 = 0
- 1 x 1 = 1
- 10 x 1 = 10
- 1000 x 1 = 1000
-
Integers (Positive and Negative Whole Numbers): The property holds true even when dealing with negative numbers.
- -5 x 1 = -5
- 1 x -20 = -20
- -100 x 1 = -100
-
Fractions: Multiplying a fraction by 1 (or any equivalent form of 1, such as 2/2, 3/3, etc.) doesn't change its value.
- (1/2) x 1 = 1/2
- (3/4) x 1 = 3/4
- (7/8) x 1 = 7/8
-
Decimals: The same principle applies to decimals.
- 2.5 x 1 = 2.5
- 0.75 x 1 = 0.75
- 3.14159 x 1 = 3.14159
-
Percentages: Percentages are essentially fractions with a denominator of 100. Multiplying a percentage by 1 doesn't change its value.
- 50% x 1 = 50% (which is equivalent to 0.50)
- 120% x 1 = 120% (which is equivalent to 1.20)
-
Algebraic Expressions: The identity property is crucial in simplifying algebraic expressions.
- x x 1 = x
- (2y + 3) x 1 = 2y + 3
- (a + b - c) x 1 = a + b - c
-
Complex Numbers: Even complex numbers, which have a real and an imaginary component, adhere to this property.
- (2 + 3i) x 1 = 2 + 3i (i represents the imaginary unit, the square root of -1)
- (5 - i) x 1 = 5 - i
Applications in Mathematics and Beyond
The identity property of multiplication might seem simple, but its applications are far-reaching:
-
Simplifying Expressions: The most direct application is in simplifying mathematical expressions. Recognizing that multiplying by 1 doesn't change the value allows us to rewrite expressions in a more convenient form. For instance, when rationalizing the denominator of a fraction, we multiply both the numerator and denominator by a form of 1 that eliminates the radical in the denominator.
-
Example: Rationalizing the denominator of 1/√2. We multiply by √2/√2 (which is equal to 1):
(1/√2) x (√2/√2) = √2 / 2. The value of the expression remains the same, but the denominator is now rational.
-
-
Solving Equations: The identity property is used implicitly when solving equations. For example, when we want to isolate a variable, we perform operations on both sides of the equation. The identity property ensures that these operations maintain the equality.
-
Example: Solving the equation 2x = 6. To isolate x, we divide both sides by 2. This is equivalent to multiplying both sides by 1/2:
(1/2) x 2x = (1/2) x 6
(1/2 * 2) * x = 3
1 * x = 3
x = 3. The identity property guarantees that multiplying 2x by 1/2 doesn't change the value of x itself (after simplification).
-
-
Understanding Mathematical Structures: The identity property is a defining characteristic of a group in abstract algebra. A group is a set of elements along with an operation (like multiplication) that satisfies certain axioms, including the existence of an identity element (like 1). The identity property is fundamental to understanding the structure and behavior of these algebraic systems.
-
Computer Programming: In programming, the identity property is used in various algorithms and data manipulations. For example, initializing a variable to 1 before performing a series of multiplications ensures that the initial value doesn't affect the final result.
-
Real-World Applications: While less direct, the concept of maintaining equivalence is crucial in many real-world scenarios. For instance, when converting units of measurement, we multiply by a conversion factor that is essentially equal to 1 (e.g., multiplying meters by 100 cm/m to convert to centimeters). This ensures that the quantity remains the same, only the units change.
Common Misconceptions
Despite its simplicity, the identity property of multiplication can sometimes be confused with other mathematical concepts. Here are a few common misconceptions:
-
Confusion with the Additive Identity: The additive identity is 0, not 1. Adding 0 to any number leaves the number unchanged (a + 0 = a). It's important to distinguish between the multiplicative and additive identities.
-
Incorrect Application to Addition: The identity property of multiplication applies only to multiplication, not addition. Multiplying a number by 0 results in 0, not the original number.
-
Overlooking the Importance of Order: While multiplication is commutative (meaning a x b = b x a), it's still important to understand the roles of the numbers involved. In the context of the identity property, multiplying by 1 means taking one 'set' of the number, not adding 1 to the number.
-
Thinking it's Too Trivial: Because it seems so obvious, the identity property is sometimes dismissed as unimportant. However, its role as a foundational principle in mathematics cannot be overstated. Its applications are woven into the fabric of more complex mathematical operations and theories.
Beyond the Basics: The Identity Property in Advanced Mathematics
While we've focused on the elementary applications of the identity property, its significance extends into more advanced areas of mathematics:
-
Linear Algebra: In linear algebra, the identity matrix (a square matrix with 1s on the main diagonal and 0s elsewhere) acts as the multiplicative identity for matrices. When a matrix is multiplied by the identity matrix, the original matrix remains unchanged. This is crucial for matrix transformations and solving systems of linear equations.
-
Abstract Algebra: As mentioned earlier, the identity property is one of the defining axioms of a group. This concept is generalized in abstract algebra to encompass a wide range of algebraic structures, including rings, fields, and vector spaces.
-
Functional Analysis: In functional analysis, the identity operator leaves a function unchanged. This operator plays a critical role in the study of linear operators and their properties.
-
Number Theory: The concept of multiplicative inverses (numbers that, when multiplied together, equal 1) is closely related to the identity property. Understanding the identity property is essential for working with modular arithmetic and cryptography.
Teaching the Identity Property
When teaching the identity property of multiplication, it's helpful to use a variety of approaches:
-
Concrete Examples: Start with simple examples using physical objects, such as counters or blocks. Show that taking one group of 5 counters results in 5 counters.
-
Visual Representations: Use diagrams or pictures to illustrate the concept of multiplication as repeated addition.
-
Real-World Scenarios: Connect the concept to real-world situations, such as calculating the cost of buying one item.
-
Hands-On Activities: Engage students in hands-on activities that involve multiplying by 1, such as measuring lengths and multiplying the measurements by 1 (in different units).
-
Games and Puzzles: Use games and puzzles to make learning fun and engaging.
-
Emphasis on Vocabulary: Clearly define the terms "identity property" and "multiplicative identity."
-
Address Misconceptions: Be aware of common misconceptions and address them explicitly.
-
Progression to Abstract Concepts: Gradually move from concrete examples to more abstract concepts, such as algebraic expressions.
The Importance of Foundational Understanding
The identity property of multiplication, though simple on the surface, is a fundamental building block for mathematical understanding. A solid grasp of this principle paves the way for success in more advanced mathematical topics and provides a valuable tool for problem-solving in various fields. By understanding why it works and how it applies across different number systems, students can develop a deeper appreciation for the elegance and consistency of mathematics. It's not just a rule to memorize; it's a key to unlocking a broader understanding of mathematical relationships.
FAQs About the Identity Property of Multiplication
Here are some frequently asked questions about the identity property of multiplication:
Q: What is the identity property of multiplication?
A: The identity property of multiplication states that any number multiplied by 1 equals that number. Mathematically, a x 1 = a and 1 x a = a.
Q: Why is 1 called the multiplicative identity?
A: Because multiplying any number by 1 "identifies" or preserves the original number's value. It doesn't change the number's identity.
Q: Does the identity property work for all numbers?
A: Yes, the identity property of multiplication holds true for all real numbers, including whole numbers, integers, fractions, decimals, and even complex numbers.
Q: Is there an identity property for addition?
A: Yes, there is. The additive identity is 0, because any number plus 0 equals that number (a + 0 = a).
Q: How is the identity property used in algebra?
A: It's used to simplify expressions and solve equations. For example, when rationalizing denominators or isolating variables, the identity property allows us to manipulate expressions without changing their underlying value.
Q: Why is understanding the identity property important?
A: It's a foundational concept that helps build a strong understanding of mathematical operations and algebraic structures. It's also used implicitly in many mathematical calculations and problem-solving techniques.
Q: Can the identity property be used with units of measurement?
A: Yes. When converting units, we multiply by a conversion factor that is equal to 1 (e.g., 1 meter = 100 centimeters). This allows us to change the units without changing the quantity.
Q: What is the difference between the identity property and the zero property of multiplication?
A: The identity property states that any number multiplied by 1 equals itself. The zero property states that any number multiplied by 0 equals 0.
Conclusion
The principle that any number multiplied by one is the number itself is more than just a simple rule; it's a cornerstone of mathematics. Its simplicity belies its profound impact, influencing everything from basic arithmetic to advanced algebraic concepts. By understanding the identity property of multiplication, we gain a deeper appreciation for the underlying structure and consistency of the mathematical world. It's a fundamental truth that empowers us to manipulate numbers, solve equations, and unlock the secrets of the universe, one calculation at a time.
Latest Posts
Latest Posts
-
Mass Of An Atom Is Determined By
Nov 18, 2025
-
How To Find Percentile With Z Score
Nov 18, 2025
-
How To Determine Whether A Function Is Odd Or Even
Nov 18, 2025
-
Difference Between Slope Intercept And Point Slope
Nov 18, 2025
-
Volume Of A Cone And Pyramid
Nov 18, 2025
Related Post
Thank you for visiting our website which covers about Any Number Multiplied By 1 Is The Number Itself . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.