A Squared Plus B Squared Plus C Squared
pinupcasinoyukle
Nov 09, 2025 · 11 min read
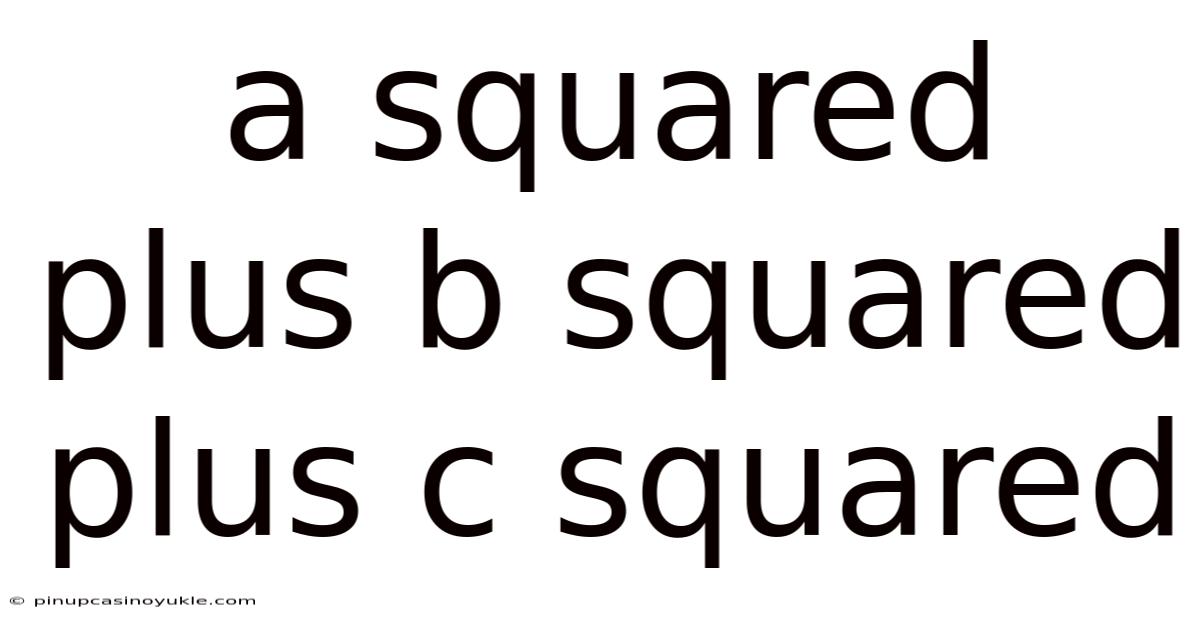
Table of Contents
The equation a² + b² + c² transcends mere algebra; it's a gateway to understanding fundamental concepts in geometry, physics, and even computer science. This seemingly simple expression unlocks a universe of possibilities, from calculating distances in three-dimensional space to representing complex data in machine learning. Let's embark on a journey to explore the depths of a² + b² + c².
Unveiling the Pythagorean Theorem in 3D
At its core, a² + b² + c² is a natural extension of the renowned Pythagorean theorem. You're likely familiar with the theorem in its two-dimensional form: a² + b² = c², where 'a' and 'b' represent the lengths of the two shorter sides (legs) of a right-angled triangle, and 'c' is the length of the longest side (hypotenuse). This equation allows us to calculate the distance between two points on a flat plane.
Now, imagine lifting that triangle into the third dimension. We now have a rectangular prism, and we want to find the length of the space diagonal, which connects one corner of the prism to the opposite corner. This is where a² + b² + c² comes into play. Here, 'a', 'b', and 'c' represent the lengths of the three sides (length, width, and height) of the rectangular prism, and the result, when square rooted, gives us the length of the space diagonal.
Derivation:
- Consider a rectangular prism with sides of length 'a', 'b', and 'c'.
- First, find the diagonal of the base (the rectangle with sides 'a' and 'b'). Using the 2D Pythagorean theorem, the length of this diagonal is √(a² + b²).
- Now, imagine a right-angled triangle formed by this base diagonal, the height 'c' of the prism, and the space diagonal we're trying to find.
- Applying the Pythagorean theorem again, we have (√(a² + b²))² + c² = d², where 'd' is the length of the space diagonal.
- Simplifying, we get a² + b² + c² = d².
- Therefore, d = √(a² + b² + c²).
This formula allows us to calculate distances in three-dimensional space, a crucial concept in fields like:
- Navigation: Calculating distances between locations on the Earth's surface, taking altitude into account.
- Computer Graphics: Determining distances between objects in a 3D virtual world for rendering and collision detection.
- Engineering: Calculating the length of structural supports in buildings and bridges.
Beyond Geometry: Vector Magnitude
The power of a² + b² + c² extends beyond simple geometric shapes. It also forms the foundation for calculating the magnitude (or length) of a vector in three-dimensional space.
A vector is a quantity that has both magnitude and direction. In three dimensions, a vector can be represented as (x, y, z), where x, y, and z are the components of the vector along the x, y, and z axes, respectively.
The magnitude of a vector (often denoted by ||v||) represents its length, irrespective of its direction. The formula for calculating the magnitude of a 3D vector is strikingly similar to our familiar equation:
||v|| = √(x² + y² + z²)
Notice the parallel? 'x', 'y', and 'z' take the place of 'a', 'b', and 'c'. This isn't a coincidence. A vector can be visualized as an arrow pointing from the origin (0, 0, 0) to the point (x, y, z). The magnitude of the vector is simply the distance between these two points, which, as we learned earlier, can be calculated using the 3D Pythagorean theorem.
Applications of Vector Magnitude:
- Physics: Determining the speed of an object moving in three dimensions. If the velocity of an object is represented by a vector, the magnitude of that vector gives its speed.
- Game Development: Calculating the speed of a character or projectile in a 3D game.
- Data Science: Calculating the Euclidean distance between data points in a three-dimensional feature space. This is a fundamental concept in clustering algorithms and other machine learning techniques.
Generalizing to N-Dimensional Space
The beauty of a² + b² + c² lies in its ability to be generalized to spaces with any number of dimensions. While we can easily visualize three dimensions, the mathematical concept of n-dimensional space allows us to represent data with 'n' attributes or features.
In n-dimensional space, a point is represented by 'n' coordinates: (x₁, x₂, x₃, ..., xₙ). The distance between two points in this space, (x₁, x₂, x₃, ..., xₙ) and (y₁, y₂, y₃, ..., yₙ), is calculated using the following formula:
Distance = √((x₁ - y₁)² + (x₂ - y₂)² + (x₃ - y₃)² + ... + (xₙ - yₙ)²)
Notice the pattern? We simply square the difference between each corresponding coordinate, sum the squares, and then take the square root. This is a direct extension of the Pythagorean theorem and our a² + b² + c² concept.
Practical Applications in Higher Dimensions:
While visualizing spaces beyond three dimensions is impossible for humans, the mathematical framework is invaluable in various fields:
- Machine Learning: In machine learning, data points are often represented as vectors in a high-dimensional space, where each dimension corresponds to a different feature or attribute. Calculating distances between these data points is essential for algorithms like k-Nearest Neighbors (k-NN) and clustering. For example, in image recognition, each image might be represented by a vector of pixel intensities. The distance between two images in this feature space can then be used to determine how similar they are.
- Data Mining: Finding patterns and relationships in large datasets often involves calculating distances between data points in a high-dimensional space. This can help identify clusters of similar customers, detect fraudulent transactions, or recommend products based on user preferences.
- Information Retrieval: Search engines use high-dimensional vector spaces to represent documents and search queries. The distance between a document vector and a query vector reflects the relevance of the document to the query.
The Sum of Squares in Statistics
The concept of the sum of squares, closely related to a² + b² + c², is fundamental in statistics. It plays a crucial role in various statistical analyses, including:
- Variance and Standard Deviation: Variance measures how spread out a set of data is around its mean. It's calculated by finding the average of the squared differences between each data point and the mean. The standard deviation is the square root of the variance and provides a more interpretable measure of spread. The sum of squares is a key component in calculating both variance and standard deviation.
- Regression Analysis: In regression analysis, we try to find the best-fitting line (or curve) that describes the relationship between two or more variables. The method of least squares is used to find this best-fitting line. This method minimizes the sum of the squared differences between the observed values and the values predicted by the regression line.
- Analysis of Variance (ANOVA): ANOVA is a statistical technique used to compare the means of two or more groups. It works by partitioning the total variance in the data into different sources of variation. The sum of squares is used to quantify the amount of variation attributable to each source.
Example: Calculating Variance
Let's say we have the following set of data: 2, 4, 6.
- Calculate the mean: (2 + 4 + 6) / 3 = 4
- Calculate the squared differences from the mean:
- (2 - 4)² = 4
- (4 - 4)² = 0
- (6 - 4)² = 4
- Calculate the sum of squares: 4 + 0 + 4 = 8
- Calculate the variance: 8 / (3-1) = 4 (We divide by n-1 for an unbiased estimate of the population variance)
- Calculate the standard deviation: √4 = 2
The sum of squares (8 in this example) is a crucial intermediate step in calculating the variance and standard deviation, which are essential for understanding the distribution of the data.
Applications in Computer Science: Image Processing and Machine Learning
The formula a² + b² + c² and its higher-dimensional generalizations have significant applications in computer science, particularly in image processing and machine learning.
Image Processing:
- Image Blurring: Many image blurring techniques use a convolution operation, where each pixel's value is replaced by a weighted average of its neighboring pixels. The weights are often determined by a Gaussian kernel, which is based on the Euclidean distance (calculated using a sum of squares) from the center pixel.
- Edge Detection: Edge detection algorithms aim to identify the boundaries between objects in an image. These algorithms often use gradient operators, which calculate the rate of change of pixel intensities in different directions. The magnitude of the gradient (a vector quantity) is calculated using the square root of the sum of squares of the gradient components in the x and y directions.
Machine Learning:
- K-Means Clustering: K-means is a popular clustering algorithm that aims to partition a set of data points into 'k' clusters. The algorithm works by iteratively assigning each data point to the nearest cluster centroid (the mean of the data points in that cluster). The distance between a data point and a cluster centroid is typically calculated using the Euclidean distance, which, as we know, involves a sum of squares.
- Support Vector Machines (SVMs): SVMs are powerful machine learning algorithms used for classification and regression. SVMs aim to find the optimal hyperplane that separates different classes of data. The distance between a data point and the hyperplane is a key factor in determining the classification of the data point. This distance calculation often involves a sum of squares.
- Principal Component Analysis (PCA): PCA is a dimensionality reduction technique that aims to find the principal components of a dataset. Principal components are orthogonal (uncorrelated) directions that capture the most variance in the data. Calculating the variance and covariance of the data, which are essential for PCA, involves sums of squares.
Beyond the Formula: Geometric Interpretation and Visualizations
While the equation a² + b² + c² is powerful in its own right, understanding its geometric interpretation can provide deeper insights.
- Sphere Equation: The equation x² + y² + z² = r² represents a sphere centered at the origin (0, 0, 0) with a radius of 'r'. This equation is a direct consequence of the 3D Pythagorean theorem. Any point (x, y, z) on the surface of the sphere is a distance 'r' away from the origin.
- Distance from the Origin: The expression √(x² + y² + z²) represents the distance of the point (x, y, z) from the origin.
- Level Sets: In multivariable calculus, level sets are sets of points where a function has a constant value. For example, the level sets of the function f(x, y, z) = x² + y² + z² are spheres centered at the origin.
Visualizing these geometric interpretations can be helpful for understanding the concepts and their applications. For example, visualizing the sphere equation can help understand the concept of distance in three dimensions.
Common Misconceptions and Pitfalls
While the concept of a² + b² + c² seems straightforward, there are some common misconceptions and pitfalls to be aware of:
- Confusing with (a + b + c)²: It's crucial to remember that a² + b² + c² is not the same as (a + b + c)². Expanding (a + b + c)² gives a² + b² + c² + 2ab + 2ac + 2bc.
- Applying to Non-Right-Angled Triangles: The Pythagorean theorem (and its 3D extension) only applies to right-angled triangles or rectangular prisms.
- Units: Always ensure that the units of 'a', 'b', and 'c' are consistent. If 'a' is in meters, 'b' and 'c' must also be in meters. The result will then be in meters squared (before taking the square root) or meters (after taking the square root).
- Computational Errors: When dealing with very large or very small numbers, numerical errors can arise during the squaring and square root operations. Consider using appropriate numerical methods to mitigate these errors.
FAQ
- What is the significance of the square root in the formula?
- The square root gives us the actual distance or magnitude. The sum of squares (a² + b² + c²) represents the squared distance.
- Can a, b, and c be negative?
- Yes, a, b, and c can be negative, especially when representing vector components. Squaring the values ensures that the distance is always positive.
- Is there a similar formula for other geometric shapes?
- While a² + b² + c² is specific to rectangular prisms and Euclidean distance, similar concepts exist for other geometric shapes. For example, calculating the surface area or volume of a complex shape often involves integrals, which can be seen as continuous sums of squares.
- How is this related to Einstein's theory of relativity?
- Einstein's theory of relativity uses a more generalized concept of distance called the spacetime interval. While it's more complex, it still involves squaring differences in coordinates and combining them in a specific way, drawing inspiration from the fundamental principles underlying a² + b² + c².
Conclusion: A Foundation of Knowledge
The equation a² + b² + c² is far more than a simple algebraic expression. It serves as a cornerstone for understanding fundamental concepts in geometry, physics, statistics, and computer science. From calculating distances in three-dimensional space to representing complex data in machine learning, this equation unlocks a wide range of applications. By understanding the underlying principles and its various applications, you gain a powerful tool for solving problems and exploring the world around you. Its elegant simplicity belies its profound impact on numerous fields of study, making it a truly remarkable and essential concept to grasp.
Latest Posts
Latest Posts
-
Write And Equation Of A Line
Nov 09, 2025
-
In What Section Would Transition Metals Be Found
Nov 09, 2025
-
What Is Shaping In Operant Conditioning
Nov 09, 2025
-
Augustus Of Primaporta Ap Art History
Nov 09, 2025
-
Covalent Bonds Are Formed Between Two Non Metals
Nov 09, 2025
Related Post
Thank you for visiting our website which covers about A Squared Plus B Squared Plus C Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.