7 As A Percentage Of 20
pinupcasinoyukle
Nov 25, 2025 · 8 min read
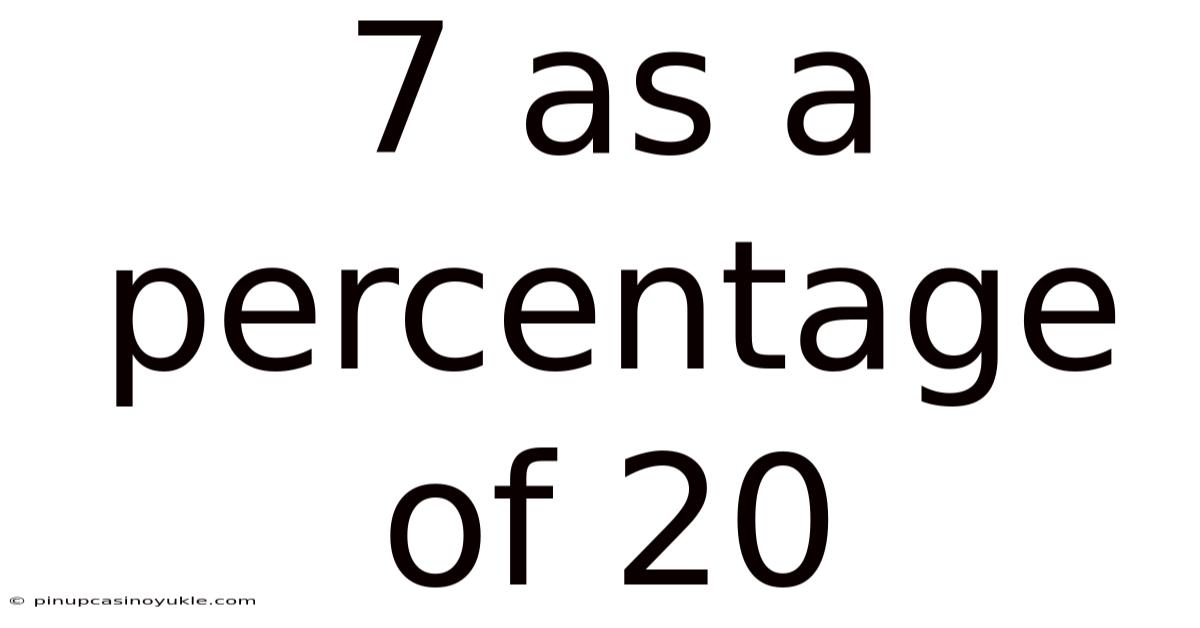
Table of Contents
Calculating percentages is a fundamental mathematical skill with applications across various aspects of life, from figuring out discounts while shopping to understanding statistics in reports. The question "7 as a percentage of 20" is a straightforward example that can help illustrate the basic principles of percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "per hundred." Essentially, when we say "X percent," we mean X out of 100. Percentages are used to express how large one quantity is relative to another quantity. To calculate a percentage, you typically divide the value you want to express as a percentage by the total value and then multiply the result by 100.
Breaking Down the Problem: 7 as a Percentage of 20
To determine what percentage 7 represents of 20, we will go through the following steps:
- Identify the Values: Determine which number is the part and which is the whole. In this case, 7 is the part, and 20 is the whole.
- Set up the Fraction: Write the part over the whole as a fraction. This gives us 7/20.
- Convert to Decimal: Divide the numerator (7) by the denominator (20) to convert the fraction into a decimal.
- Multiply by 100: Multiply the decimal by 100 to convert it into a percentage.
- Add the Percent Sign: Append the percent sign (%) to the result to indicate that it is a percentage.
Let's execute these steps:
Step 1: Identify the Values
The problem states "7 as a percentage of 20." Here, 7 is the number we want to express as a percentage, and 20 is the total or whole amount. So, part = 7 and whole = 20.
Step 2: Set up the Fraction
To express 7 as a fraction of 20, we write it as: 7/20
This fraction represents the ratio of 7 to 20.
Step 3: Convert to Decimal
Now, we need to convert the fraction 7/20 into a decimal. To do this, we divide the numerator (7) by the denominator (20):
7 ÷ 20 = 0.35
Step 4: Multiply by 100
Next, we convert the decimal 0.35 into a percentage by multiplying it by 100:
- 35 x 100 = 35
Step 5: Add the Percent Sign
Finally, we add the percent sign (%) to the result to indicate that it is a percentage:
35%
Therefore, 7 is 35% of 20.
Alternative Method: Proportion
Another way to solve this problem is by setting up a proportion. A proportion is an equation that states that two ratios are equal. In this case, we want to find the percentage x such that:
7/20 = x/100
To solve for x, we can cross-multiply:
20 * x = 7 * 100
20x = 700
Now, divide both sides by 20 to isolate x:
x = 700 / 20
x = 35
Thus, 7 is 35% of 20.
Real-World Applications
Understanding how to calculate percentages is incredibly useful in many real-world scenarios. Here are a few examples:
Shopping Discounts
When you are shopping, stores often advertise discounts as percentages. For example, a store might offer "20% off" on a particular item. If the original price of the item is $20 and you want to know how much money you will save, you calculate 20% of $20:
20/100 * $20 = 0.20 * $20 = $4
So, you would save $4 on the item, and the new price would be $16.
Sales Tax
Sales tax is often calculated as a percentage of the purchase price. For example, if the sales tax rate is 7% and you buy an item for $20, the sales tax would be:
7/100 * $20 = 0.07 * $20 = $1.40
The total cost of the item would then be $20 + $1.40 = $21.40.
Grades and Scores
In education, grades are often expressed as percentages. If you get 7 out of 20 questions correct on a quiz, your score would be:
(7/20) * 100 = 35%
Financial Investments
When evaluating financial investments, returns are often expressed as percentages. If you invest $20 and earn $7 in profit, your return on investment (ROI) would be:
(7/20) * 100 = 35%
This means you have earned a 35% return on your investment.
Data Analysis
Percentages are widely used in data analysis to summarize and interpret data. For example, if you survey 20 people and 7 of them prefer a particular product, you can say that 35% of the people surveyed prefer that product.
Common Mistakes to Avoid
When calculating percentages, it's essential to avoid common mistakes to ensure accurate results. Here are a few to watch out for:
Confusing Part and Whole
One of the most common mistakes is confusing the part and the whole. Always make sure you are dividing the correct number by the correct total. In the problem "7 as a percentage of 20," 7 is the part and 20 is the whole.
Incorrect Decimal Conversion
When converting a fraction to a decimal, make sure you perform the division correctly. A small error in the division can lead to a significant difference in the final percentage.
Forgetting to Multiply by 100
After converting the fraction to a decimal, remember to multiply by 100 to express the number as a percentage. Forgetting this step will give you a decimal value instead of a percentage.
Not Adding the Percent Sign
Always add the percent sign (%) to the final result to indicate that it is a percentage. This helps avoid confusion and clearly communicates that the number represents a part out of 100.
Rounding Errors
When dealing with decimals that go on for many digits, rounding can introduce errors. It's important to round correctly and consistently. If you need a precise result, avoid rounding until the very end of the calculation.
Tips for Mastering Percentage Calculations
Here are some tips to help you master percentage calculations:
Practice Regularly
The more you practice, the more comfortable you will become with percentage calculations. Try solving different types of percentage problems regularly to reinforce your understanding.
Understand the Basics
Make sure you have a solid understanding of the basic concepts of fractions, decimals, and percentages. These concepts are interconnected, and a strong foundation will make it easier to solve more complex problems.
Use Real-World Examples
Apply percentage calculations to real-world situations to see how they are used in everyday life. This can help you appreciate the practical value of understanding percentages.
Check Your Work
Always double-check your work to make sure you haven't made any mistakes. This is especially important in situations where accuracy is critical, such as financial calculations.
Use Tools and Resources
Take advantage of online tools and resources, such as percentage calculators and tutorials, to help you learn and practice percentage calculations.
Advanced Percentage Problems
Once you have a solid understanding of the basics, you can tackle more advanced percentage problems. Here are a few examples:
Percentage Increase and Decrease
Percentage increase and decrease problems involve calculating the change in a value as a percentage of the original value. For example, if a price increases from $20 to $27, the percentage increase is:
(($27 - $20) / $20) * 100 = (7/20) * 100 = 35%
So, the price has increased by 35%.
Finding the Original Value
Sometimes, you may need to find the original value when you know the percentage and the resulting value. For example, if you know that $7 is 35% of the original value, you can find the original value by setting up the equation:
- 35 * Original Value = $7
Original Value = $7 / 0.35 = $20
Compound Percentage Changes
Compound percentage changes involve applying multiple percentage changes in sequence. For example, if a price increases by 10% and then decreases by 5%, the overall percentage change is not simply 10% - 5% = 5%. Instead, you need to calculate each change separately:
Initial Price: $100
After 10% increase: $100 + (10/100 * $100) = $110
After 5% decrease: $110 - (5/100 * $110) = $104.50
Overall Change: (($104.50 - $100) / $100) * 100 = 4.5%
So, the overall price has increased by 4.5%.
The Importance of Estimation
Estimation is a valuable skill when working with percentages. It allows you to quickly check whether your calculated answer is reasonable. For example, if you are calculating 7 as a percentage of 20, you can estimate that since 7 is a little more than one-third of 20, the percentage should be a little more than 33%. This is close to the actual answer of 35%, so you can be confident that your calculation is correct.
Conclusion
Calculating percentages is a fundamental skill with wide-ranging applications in everyday life. By understanding the basic principles and practicing regularly, you can master percentage calculations and confidently apply them in various situations. The problem "7 as a percentage of 20" is a simple example that illustrates the core concepts. Remember to identify the part and the whole, set up the fraction, convert to a decimal, multiply by 100, and add the percent sign. Avoid common mistakes, and use real-world examples to reinforce your understanding. With these skills, you will be well-equipped to handle percentage calculations in any context.
Latest Posts
Latest Posts
-
Lesson 5 Homework Practice Negative Exponents Answer Key
Nov 25, 2025
-
Split Stems Stem And Leaf Plot
Nov 25, 2025
-
What Is The Lub Dub Sound Of The Heart
Nov 25, 2025
-
How To Do Good On The Sat
Nov 25, 2025
-
White House Staff Ap Gov Definition
Nov 25, 2025
Related Post
Thank you for visiting our website which covers about 7 As A Percentage Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.