60 Is What Percent Of 15
pinupcasinoyukle
Nov 11, 2025 · 9 min read
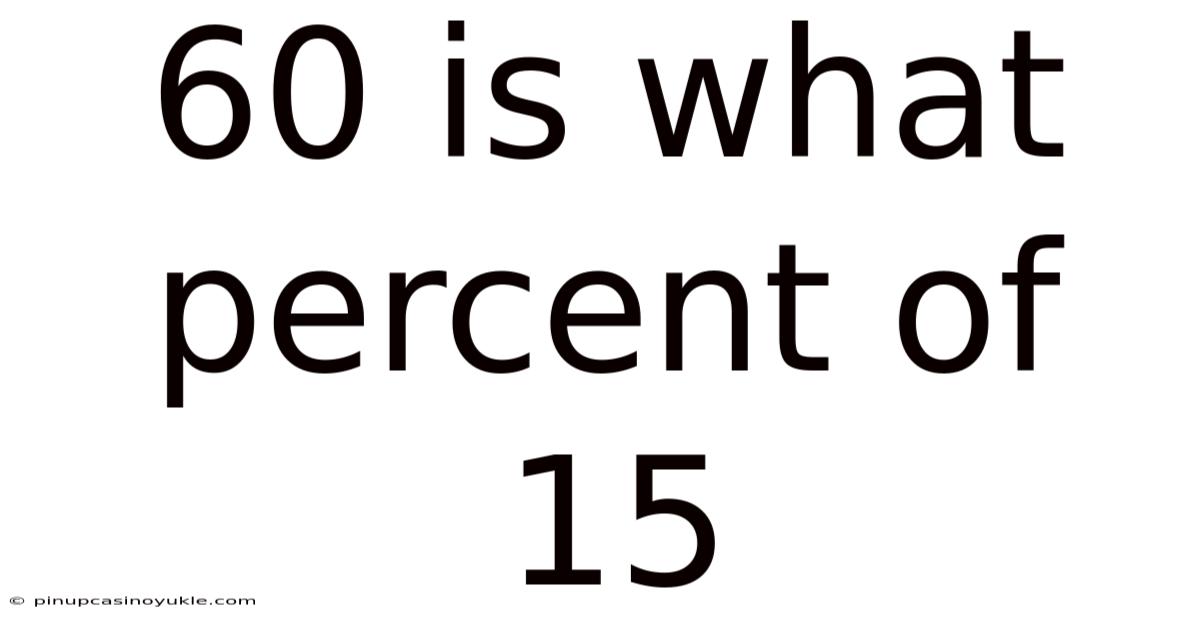
Table of Contents
Calculating percentages is a fundamental skill with wide-ranging applications, from calculating discounts at your favorite store to understanding financial reports. When you need to figure out "60 is what percent of 15," you're essentially asking, "How many times does 15 fit into 60, expressed as a percentage?" This question involves a straightforward calculation that can be easily mastered.
Understanding the Basics of Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "per hundred." Therefore, calculating percentages involves finding out how a part relates to a whole, with the whole being considered as 100%.
The Formula for Calculating Percentages
The basic formula to find what percentage one number is of another is:
$ \text{Percentage} = \left( \frac{\text{Part}}{\text{Whole}} \right) \times 100 $
Where:
- Part is the number you want to express as a percentage of another number.
- Whole is the total or the reference number you are comparing the part to.
Step-by-Step Calculation: 60 is What Percent of 15?
To solve "60 is what percent of 15," we need to identify which number is the part and which is the whole. In this case:
- Part = 60
- Whole = 15
Now, let's plug these values into our formula:
$ \text{Percentage} = \left( \frac{60}{15} \right) \times 100 $
Step 1: Divide the Part by the Whole
First, divide 60 by 15:
$ \frac{60}{15} = 4 $
Step 2: Multiply by 100
Next, multiply the result by 100 to convert it into a percentage:
$ 4 \times 100 = 400 $
Therefore, 60 is 400% of 15.
Real-World Applications of Percentage Calculations
Understanding how to calculate percentages is useful in many everyday situations. Here are a few examples:
1. Retail Discounts
Imagine a store is offering a 20% discount on an item that originally costs $50. To find the discount amount, you calculate 20% of $50:
$ \text{Discount} = \left( \frac{20}{100} \right) \times 50 = 0.20 \times 50 = $10 $
So, the discount is $10, and the final price is $50 - $10 = $40.
2. Sales Tax
If you buy an item for $100 and the sales tax is 8%, the tax amount is:
$ \text{Tax} = \left( \frac{8}{100} \right) \times 100 = 0.08 \times 100 = $8 $
The total cost of the item is $100 + $8 = $108.
3. Grade Calculation
Suppose you scored 80 out of 100 on a test. Your percentage score is:
$ \text{Percentage} = \left( \frac{80}{100} \right) \times 100 = 80% $
4. Financial Analysis
In finance, percentages are used to calculate returns on investment, profit margins, and more. For example, if an investment of $1,000 yields a profit of $50, the return on investment is:
$ \text{Return} = \left( \frac{50}{1000} \right) \times 100 = 5% $
5. Statistical Data
Percentages are commonly used to present statistical data. For instance, if a survey of 500 people shows that 350 prefer coffee over tea, the percentage of people who prefer coffee is:
$ \text{Percentage} = \left( \frac{350}{500} \right) \times 100 = 70% $
Common Mistakes to Avoid When Calculating Percentages
While the formula for calculating percentages is straightforward, there are common mistakes that people often make. Being aware of these can help you avoid errors.
1. Incorrectly Identifying the Part and the Whole
One of the most common mistakes is confusing the part and the whole. Always ensure that you correctly identify which number you are expressing as a percentage of the other. For example, if the question is "What percent of 50 is 10?", 10 is the part and 50 is the whole.
2. Forgetting to Multiply by 100
After dividing the part by the whole, you must multiply the result by 100 to express it as a percentage. Forgetting this step will give you a decimal or fraction, not a percentage.
3. Misinterpreting Percentage Increase or Decrease
When calculating percentage increase or decrease, make sure you use the correct base value. For example, if a price increases from $20 to $25, the percentage increase is calculated as:
$ \text{Increase} = \left( \frac{\text{New Value} - \text{Old Value}}{\text{Old Value}} \right) \times 100 $
$ \text{Increase} = \left( \frac{25 - 20}{20} \right) \times 100 = \left( \frac{5}{20} \right) \times 100 = 25% $
4. Rounding Errors
When dealing with decimals, rounding errors can occur. It’s best to keep as many decimal places as possible during the calculation and round only at the final step to get a more accurate result.
Advanced Percentage Calculations
Beyond the basic formula, there are more complex percentage calculations that you might encounter.
1. Percentage Change
Percentage change is used to determine the extent to which a quantity changes over time. The formula is:
$ \text{Percentage Change} = \left( \frac{\text{New Value} - \text{Old Value}}{\text{Old Value}} \right) \times 100 $
For example, if a company's revenue increases from $1 million to $1.2 million, the percentage change is:
$ \text{Percentage Change} = \left( \frac{1.2 - 1}{1} \right) \times 100 = 20% $
2. Compound Interest
Compound interest is the interest calculated on the initial principal, which also includes all of the accumulated interest from previous periods. The formula for compound interest is:
$ A = P \left(1 + \frac{r}{n}\right)^{nt} $
Where:
- ( A ) = the future value of the investment/loan, including interest
- ( P ) = the principal investment amount (the initial deposit or loan amount)
- ( r ) = the annual interest rate (as a decimal)
- ( n ) = the number of times that interest is compounded per year
- ( t ) = the number of years the money is invested or borrowed for
For example, if you invest $1,000 at an annual interest rate of 5% compounded annually for 10 years:
$ A = 1000 \left(1 + \frac{0.05}{1}\right)^{1 \times 10} = 1000 \times (1.05)^{10} \approx $1,628.89 $
3. Calculating Margins
In business, margins are often expressed as percentages. Gross profit margin, for example, is calculated as:
$ \text{Gross Profit Margin} = \left( \frac{\text{Revenue} - \text{Cost of Goods Sold}}{\text{Revenue}} \right) \times 100 $
If a company has a revenue of $500,000 and a cost of goods sold of $300,000, the gross profit margin is:
$ \text{Gross Profit Margin} = \left( \frac{500,000 - 300,000}{500,000} \right) \times 100 = \left( \frac{200,000}{500,000} \right) \times 100 = 40% $
Tips for Mastering Percentage Calculations
Mastering percentage calculations requires practice and a clear understanding of the underlying concepts. Here are some tips to help you improve your skills:
1. Practice Regularly
Like any mathematical skill, practice makes perfect. Work through various examples and real-world problems to build your confidence.
2. Use Online Calculators and Tools
There are many online percentage calculators and tools available that can help you check your work and speed up calculations. These tools are especially useful for complex calculations or when dealing with large numbers.
3. Break Down Complex Problems
When faced with a complex problem involving percentages, break it down into smaller, more manageable steps. This will make the problem less daunting and reduce the likelihood of errors.
4. Understand the Context
Always consider the context of the problem. Understanding what the numbers represent and how they relate to each other will help you avoid common mistakes and ensure that your calculations are accurate.
5. Check Your Answers
Whenever possible, check your answers to ensure they are reasonable. If you're calculating a discount, make sure the final price is less than the original price. If you're calculating a percentage increase, make sure the new value is higher than the old value.
Why Are Percentages Important?
Percentages are more than just numbers; they are a fundamental tool for understanding and interpreting the world around us. Their importance spans various aspects of life, from personal finance to professional decision-making. Here's why understanding percentages is crucial:
1. Financial Literacy
Percentages are essential for financial literacy. They help individuals understand interest rates on loans, investment returns, and discounts on purchases. Without a solid grasp of percentages, it's challenging to make informed financial decisions, potentially leading to poor budgeting, overspending, or missed investment opportunities.
2. Informed Decision-Making
In everyday life, percentages enable informed decision-making. Whether it's comparing prices, understanding survey results, or evaluating health statistics, percentages provide a clear and standardized way to assess information. For example, knowing the percentage of calories from fat in a food product helps consumers make healthier dietary choices.
3. Business and Economics
Businesses rely heavily on percentages for analyzing data, tracking performance, and making strategic decisions. Profit margins, market share, growth rates, and customer satisfaction are all expressed as percentages. These metrics help businesses identify trends, measure success, and adjust their strategies accordingly.
4. Science and Statistics
In scientific research and statistical analysis, percentages are used to present and interpret data. They provide a way to standardize findings, making it easier to compare results across different studies. Percentages are also used to calculate probabilities, assess risk, and draw conclusions from experiments.
5. Education and Learning
Percentages are fundamental in education, from grading assignments to evaluating student performance. They provide a fair and consistent way to assess knowledge and track progress. Understanding percentages also helps students develop critical thinking skills and prepare for future academic and professional challenges.
6. Public Policy and Governance
Governments use percentages to analyze economic data, track social trends, and evaluate the effectiveness of policies. Unemployment rates, inflation rates, and poverty rates are all expressed as percentages. These metrics help policymakers make informed decisions and allocate resources effectively.
Practical Examples of Percentage Calculations
Let's explore more practical examples to solidify your understanding of percentage calculations:
Example 1: Calculating a Tip
You have a restaurant bill of $45.50, and you want to leave a 15% tip. How much should you tip?
$ \text{Tip Amount} = \left( \frac{15}{100} \right) \times 45.50 = 0.15 \times 45.50 = $6.83 $
So, you should leave a tip of $6.83.
Example 2: Finding the Original Price After a Discount
A store is offering a 30% discount on a jacket, and the sale price is $63. What was the original price of the jacket?
Let ( x ) be the original price. Then:
$ x - 0.30x = 63 $
$ 0.70x = 63 $
$ x = \frac{63}{0.70} = $90 $
The original price of the jacket was $90.
Example 3: Calculating Percentage of Attendance
A school has 1,200 students, and 1,080 students attended a particular event. What percentage of students attended the event?
$ \text{Percentage} = \left( \frac{1080}{1200} \right) \times 100 = 0.9 \times 100 = 90% $
90% of the students attended the event.
Example 4: Determining Weight Loss Percentage
Someone weighed 200 pounds and lost 15 pounds. What is the percentage of weight loss?
$ \text{Percentage Loss} = \left( \frac{15}{200} \right) \times 100 = 0.075 \times 100 = 7.5% $
The person lost 7.5% of their weight.
Conclusion
Calculating percentages is a versatile skill with applications in various aspects of life. Whether you're figuring out discounts, analyzing financial data, or interpreting statistical information, understanding percentages is essential for making informed decisions. By mastering the basic formula, avoiding common mistakes, and practicing regularly, you can confidently tackle any percentage-related problem. So, when you ask, "60 is what percent of 15?", remember the simple steps and the broader context of how percentages impact our daily lives.
Latest Posts
Latest Posts
-
Base And Height Of A Triangle
Nov 12, 2025
-
Is 79 A Prime Number Or A Composite Number
Nov 12, 2025
-
What Is The Product Of Light Dependent Reaction
Nov 12, 2025
-
How Do I Square A Fraction
Nov 12, 2025
-
What Is The Difference Between Population And Community
Nov 12, 2025
Related Post
Thank you for visiting our website which covers about 60 Is What Percent Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.