5 Of 20 Is What Percent
pinupcasinoyukle
Nov 28, 2025 · 7 min read
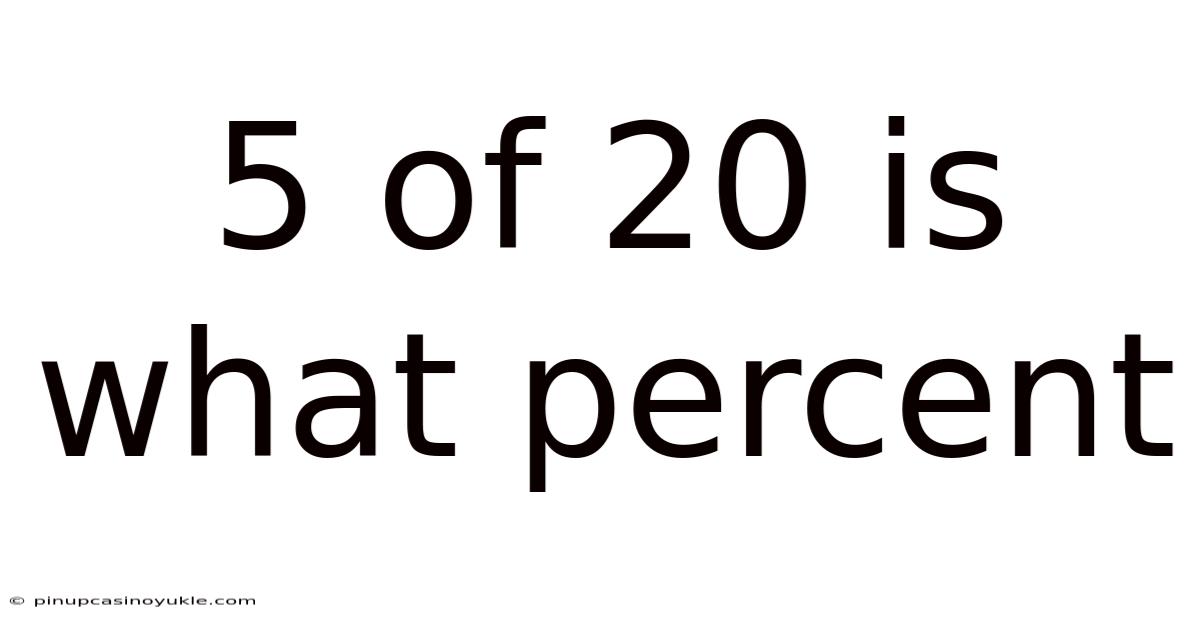
Table of Contents
Five out of 20, expressed as a percentage, unveils a fundamental aspect of proportions, vital across diverse fields from everyday calculations to advanced statistical analysis. Understanding how to convert fractions like 5/20 into percentages is not just a mathematical exercise; it’s a practical skill that enhances comprehension in finance, statistics, and various scientific disciplines.
Decoding Percentages: The Basics
The concept of a percentage is rooted in expressing a number as a fraction of 100. Essentially, a percentage tells us how many parts out of 100 we have. The term "percent" comes from the Latin "per centum," meaning "out of one hundred." This makes percentages a standardized way to compare different ratios and proportions.
Why Percentages Matter
Percentages offer a clear and universal way to understand proportions:
- Standardization: They allow for easy comparison of different fractions.
- Clarity: Percentages simplify complex ratios, making them more understandable.
- Versatility: They are applicable in numerous contexts, including finance, statistics, and everyday life.
The Process: Converting 5/20 to a Percentage
Converting 5 out of 20 to a percentage involves a straightforward calculation that reveals what portion 5 represents when the total is considered as 100.
Step-by-Step Conversion
- Form the Fraction: Start with the fraction 5/20.
- Divide: Divide the numerator (5) by the denominator (20). This gives you a decimal.
- 5 ÷ 20 = 0.25
- Multiply by 100: Multiply the decimal by 100 to convert it into a percentage.
-
- 25 x 100 = 25%
-
Therefore, 5 out of 20 is equal to 25%.
Alternative Method: Simplification and Multiplication
Another approach involves simplifying the fraction before converting it:
- Simplify the Fraction: Reduce 5/20 to its simplest form. Both 5 and 20 are divisible by 5.
- 5/20 = 1/4
- Convert to Percentage: Recognize that 1/4 is a common fraction equivalent to 25%. Alternatively, divide 1 by 4 and multiply by 100.
- 1 ÷ 4 = 0.25
-
- 25 x 100 = 25%
This method provides a quicker way to find the percentage, especially when dealing with easily simplified fractions.
Real-World Applications
Understanding how to calculate percentages is invaluable in numerous real-world scenarios.
Financial Analysis
In finance, percentages are used to calculate returns on investments, interest rates, and profit margins:
- Investment Returns: If an investment of $20 grows by $5, the return on investment is 25%.
- Discounts: A 25% discount on an item originally priced at $20 means a savings of $5.
Academic Grading
Teachers often use percentages to grade assignments and exams. For example, scoring 5 out of 20 on a quiz means earning 25%.
Statistical Analysis
Percentages are used to represent data in a more understandable way:
- Market Share: If a company captures 5 out of 20 customers in a market, its market share is 25%.
- Survey Results: In a survey of 20 people, if 5 support a particular view, that view is supported by 25% of the respondents.
Daily Life
Percentages frequently appear in everyday situations such as:
- Sales Tax: Calculating the sales tax on a purchase.
- Tipping: Determining the appropriate tip amount at a restaurant.
- Understanding Nutritional Information: Assessing the percentage of daily recommended values in food products.
Common Pitfalls and How to Avoid Them
While calculating percentages is generally straightforward, some common errors can occur.
Misunderstanding the Base
One frequent mistake is misunderstanding what constitutes the "whole" or the base number. For instance, confusing the part with the whole can lead to incorrect percentage calculations. Always ensure you are dividing by the correct total to get an accurate percentage.
Calculation Errors
Simple arithmetic errors can also lead to incorrect percentages. Double-checking your calculations, especially when dealing with large numbers or complex fractions, is always a good practice.
Incorrect Application
Applying the percentage to the wrong context can lead to misinterpretations. Always ensure that the percentage is relevant to the situation at hand.
Advanced Applications of Percentages
Beyond basic calculations, percentages are used in more advanced mathematical and statistical contexts.
Percentage Change
Calculating percentage change is crucial in many fields to understand growth or decline:
- Formula: Percentage Change = [(New Value - Old Value) / Old Value] x 100
- Example: If a company’s revenue increases from $20 to $25, the percentage change is [(25 - 20) / 20] x 100 = 25%.
Compound Interest
Understanding percentages is essential for calculating compound interest, where interest is earned not only on the initial principal but also on the accumulated interest from previous periods.
Statistical Analysis
In statistics, percentages are used to describe distributions, compare data sets, and interpret research findings. They provide a standardized way to present complex data in an understandable format.
Examples and Practice Problems
To solidify your understanding, let’s work through some examples and practice problems.
Example 1: Calculating a Discount
A store offers a 15% discount on an item priced at $80. How much is the discount?
- Calculation: 15% of $80 = (15/100) x $80 = $12
- Answer: The discount is $12.
Example 2: Finding Percentage of Students
In a class of 40 students, 10 are absent. What percentage of students are absent?
- Calculation: (10/40) x 100 = 25%
- Answer: 25% of the students are absent.
Practice Problems
- What is 30% of 50?
- If you scored 18 out of 25 on a test, what is your percentage score?
- A shirt is on sale for 20% off its original price of $45. What is the sale price?
- Convert 7/25 to a percentage.
- In a survey of 200 people, 80 prefer coffee over tea. What percentage prefers coffee?
The Mathematical Foundation
The conversion of fractions to percentages is grounded in fundamental mathematical principles.
Understanding Ratios and Proportions
A fraction represents a ratio between two quantities. Converting a fraction to a percentage involves scaling this ratio to a base of 100, providing a standardized measure for comparison.
The Role of the Base
The base (denominator) in a fraction is crucial because it defines the whole. When converting to a percentage, we are essentially asking: "How many parts out of 100 does the numerator represent?"
The Decimal Connection
Converting a fraction to a decimal is an intermediate step that simplifies the conversion to a percentage. The decimal provides a numerical value that can be easily scaled to 100.
Tips for Mastering Percentage Calculations
Mastering percentage calculations involves understanding the underlying principles and practicing regularly.
Understand the Basics
Ensure you have a solid understanding of fractions, decimals, and ratios. These concepts are fundamental to percentage calculations.
Practice Regularly
Consistent practice is key to mastering percentage calculations. Work through various examples and real-world problems to reinforce your understanding.
Use Mental Math
Develop your mental math skills to quickly estimate percentages. This can be particularly useful in everyday situations where a calculator is not readily available.
Utilize Tools and Resources
Take advantage of online calculators, tutorials, and educational resources to enhance your understanding and skills.
Simplifying Complex Scenarios
Percentages can also be used to simplify complex scenarios by providing a clear and understandable way to represent proportions and changes.
Comparative Analysis
Percentages allow for easy comparison of different data sets. For example, comparing the growth rates of different companies becomes straightforward when expressed as percentages.
Trend Analysis
Analyzing trends over time is simplified with percentages. Tracking percentage changes in sales, revenue, or market share can provide valuable insights for decision-making.
Risk Assessment
In finance and insurance, percentages are used to assess and communicate risk. For example, expressing the probability of an event occurring as a percentage provides a clear and understandable measure of risk.
Conclusion: The Power of Percentages
Understanding how to convert fractions to percentages, such as converting 5 out of 20 to 25%, is a fundamental skill with wide-ranging applications. From financial analysis and academic grading to statistical analysis and everyday decision-making, percentages provide a clear and standardized way to understand proportions and changes. By mastering the basic principles, practicing regularly, and understanding the common pitfalls, you can harness the power of percentages to enhance your analytical and problem-solving skills.
Latest Posts
Latest Posts
-
Power Of A Power Property Examples
Nov 28, 2025
-
What Is The Period On A Graph
Nov 28, 2025
-
What Is A Relative Minimum On A Graph
Nov 28, 2025
-
Difference Between Enumerated And Implied Powers
Nov 28, 2025
-
Converting A Fraction To A Repeating Decimal
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about 5 Of 20 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.