5 Is What Percent Of 8
pinupcasinoyukle
Nov 08, 2025 · 7 min read
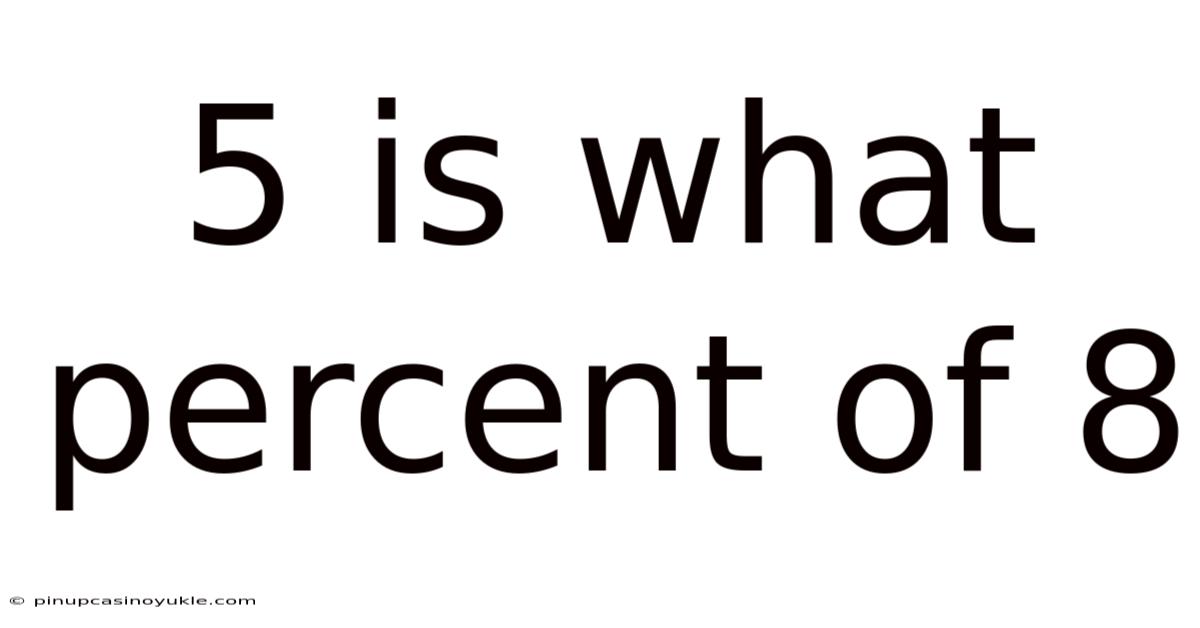
Table of Contents
Calculating percentages is a fundamental skill applicable in various real-life scenarios, from figuring out discounts while shopping to understanding statistical data. When faced with a question like "5 is what percent of 8," it's essential to approach it with a clear understanding of the underlying principles. This article will guide you through the process of solving this problem, provide practical examples, and discuss the importance of understanding percentages in everyday life.
Understanding the Basics of Percentages
Percentages are a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin "per centum," meaning "out of one hundred." When we say "x percent," we mean x out of 100, which can be written as x/100.
To solve "5 is what percent of 8," we need to determine what fraction of 8 is equal to 5, and then convert that fraction into a percentage. The formula to calculate this is:
Percentage = (Part / Whole) * 100
In this case:
- Part = 5
- Whole = 8
Step-by-Step Calculation
Let’s walk through the calculation step by step:
- Set up the Fraction:
-
Write the fraction with the part (5) as the numerator and the whole (8) as the denominator:
5/8
-
- Convert the Fraction to a Decimal:
-
Divide the numerator by the denominator:
5 ÷ 8 = 0.625
-
- Convert the Decimal to a Percentage:
-
Multiply the decimal by 100:
0. 625 * 100 = 62.5
-
So, 5 is 62.5% of 8.
Detailed Explanation of Each Step
Setting up the Fraction
The initial step in solving any percentage problem involves correctly identifying the "part" and the "whole." The "whole" is the total amount or the reference value, while the "part" is the portion of that whole that we are interested in.
In our problem, "5 is what percent of 8," the number 8 is the whole because we are trying to find out what percentage of 8 equals 5. The number 5 is the part, as it represents the portion of 8 we are concerned with.
Setting up the fraction correctly is crucial because it determines the accuracy of the subsequent steps. The fraction 5/8 represents the ratio of the part to the whole, which is the foundation for calculating the percentage.
Converting the Fraction to a Decimal
To convert the fraction 5/8 to a decimal, we perform the division 5 ÷ 8. This division gives us a decimal value that represents the same proportion as the fraction but in a different format.
When we divide 5 by 8, we get 0.625. This decimal value is essential because it allows us to easily convert the fraction into a percentage. Decimals are base-10 numbers, making them straightforward to work with when calculating percentages.
Converting the Decimal to a Percentage
The final step involves converting the decimal 0.625 into a percentage. To do this, we multiply the decimal by 100. The reason we multiply by 100 is that percentages are expressed as parts per hundred.
0. 625 * 100 = 62.5
This calculation tells us that 5 is 62.5% of 8. The percentage sign (%) is added to indicate that the number is expressed as a percentage.
Real-World Examples
Understanding how to calculate percentages is incredibly useful in everyday life. Here are a few examples:
-
Discounts:
- Suppose an item originally priced at $8 is on sale for $5. To find the percentage discount, you would calculate:
- Discount Amount = $8 - $5 = $3
- Percentage Discount = (3/8) * 100 = 37.5%
- Suppose an item originally priced at $8 is on sale for $5. To find the percentage discount, you would calculate:
-
Test Scores:
-
If you score 5 out of 8 questions correctly on a quiz, your percentage score is:
- (5/8) * 100 = 62.5%
-
-
Financial Analysis:
-
If a company's expenses are $5 million and its revenue is $8 million, the expenses as a percentage of revenue are:
- (5/8) * 100 = 62.5%
-
-
Cooking:
-
If a recipe calls for 8 ounces of flour and you only use 5 ounces, you've used:
- (5/8) * 100 = 62.5% of the required flour
-
Why Understanding Percentages is Important
-
Financial Literacy:
- Percentages are crucial for understanding interest rates, loan terms, investment returns, and budget allocations. Knowing how to calculate percentages helps you make informed financial decisions.
-
Data Interpretation:
- Statistics often involve percentages. Understanding percentages allows you to interpret data presented in reports, surveys, and studies accurately.
-
Informed Decision-Making:
- Whether you're comparing prices, assessing risks, or evaluating performance, percentages provide a standardized way to compare different quantities and make informed decisions.
-
Everyday Math:
- From calculating tips at restaurants to understanding sales tax, percentages are a fundamental part of everyday math.
Common Mistakes to Avoid
-
Incorrectly Identifying the Part and Whole:
- One of the most common mistakes is confusing the part and the whole. Always make sure you understand which number represents the total amount and which represents the portion of that total.
-
Forgetting to Multiply by 100:
- After dividing the part by the whole, remember to multiply the result by 100 to convert the decimal into a percentage. Failing to do so will give you the decimal value, not the percentage.
-
Rounding Errors:
- When dealing with decimals, be mindful of rounding errors. Rounding too early in the calculation can lead to inaccuracies in the final percentage.
-
Misinterpreting the Question:
- Sometimes, the wording of the problem can be confusing. Take the time to understand exactly what the question is asking before attempting to solve it.
Advanced Applications of Percentages
Beyond the basics, percentages are used in more complex calculations and analyses. Here are a few advanced applications:
-
Percentage Change:
-
Percentage change is used to calculate the relative change in a quantity over time. The formula is:
- Percentage Change = [(New Value - Old Value) / Old Value] * 100
-
-
Compound Interest:
-
Compound interest involves calculating interest on the initial principal and the accumulated interest from previous periods. The formula is:
-
A = P (1 + r/n)^(nt)
- Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (as a decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
- Where:
-
-
-
Statistical Analysis:
- Percentages are used extensively in statistical analysis to represent proportions, probabilities, and confidence intervals.
Examples with Detailed Solutions
Let's explore some more examples to solidify your understanding:
Example 1: Calculating Sales Tax
-
Problem: You buy an item for $50, and the sales tax is 8%. How much is the sales tax amount, and what is the total cost?
- Solution:
-
Calculate the sales tax amount:
- Sales Tax Amount = (8/100) * $50 = $4
-
Calculate the total cost:
- Total Cost = $50 + $4 = $54
-
- Solution:
Example 2: Determining Profit Margin
-
Problem: A business sells a product for $25, and the cost to produce it is $15. What is the profit margin as a percentage of the selling price?
- Solution:
-
Calculate the profit:
- Profit = $25 - $15 = $10
-
Calculate the profit margin:
- Profit Margin = (10/25) * 100 = 40%
-
- Solution:
Example 3: Calculating Percentage Increase
-
Problem: A company's revenue increased from $100,000 to $120,000. What is the percentage increase?
- Solution:
-
Calculate the increase in revenue:
- Increase = $120,000 - $100,000 = $20,000
-
Calculate the percentage increase:
- Percentage Increase = (20,000/100,000) * 100 = 20%
-
- Solution:
Tips for Mastering Percentage Calculations
-
Practice Regularly:
- The more you practice, the more comfortable you'll become with percentage calculations. Work through various problems and real-life scenarios.
-
Use Visual Aids:
- Visual aids like pie charts and bar graphs can help you visualize percentages and understand their relative sizes.
-
Break Down Complex Problems:
- If you're faced with a complex problem involving percentages, break it down into smaller, more manageable steps.
-
Double-Check Your Work:
- Always double-check your calculations to ensure accuracy. Pay attention to details and avoid common mistakes.
-
Use Online Resources:
- There are many online resources, such as calculators and tutorials, that can help you with percentage calculations.
Conclusion
Understanding how to calculate percentages is an essential skill that has wide-ranging applications in everyday life. By mastering the basic principles and practicing regularly, you can confidently solve percentage problems and make informed decisions in various situations. Whether you're calculating discounts, analyzing data, or managing your finances, a solid understanding of percentages is invaluable. Remember the formula: Percentage = (Part / Whole) * 100, and you'll be well-equipped to tackle any percentage-related challenge.
Latest Posts
Latest Posts
-
What Are The Three Checkpoints Of The Cell Cycle
Nov 08, 2025
-
Integrated Rate Equation For Zero Order Reaction
Nov 08, 2025
-
Periodic Table Of Elements Ionization Energy
Nov 08, 2025
-
Pcr Is Dependent On A Heat Stable
Nov 08, 2025
-
All Cells Come From Preexisting Cells
Nov 08, 2025
Related Post
Thank you for visiting our website which covers about 5 Is What Percent Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.