5 6 Divided By 1 4 In Fraction Form
pinupcasinoyukle
Nov 26, 2025 · 9 min read
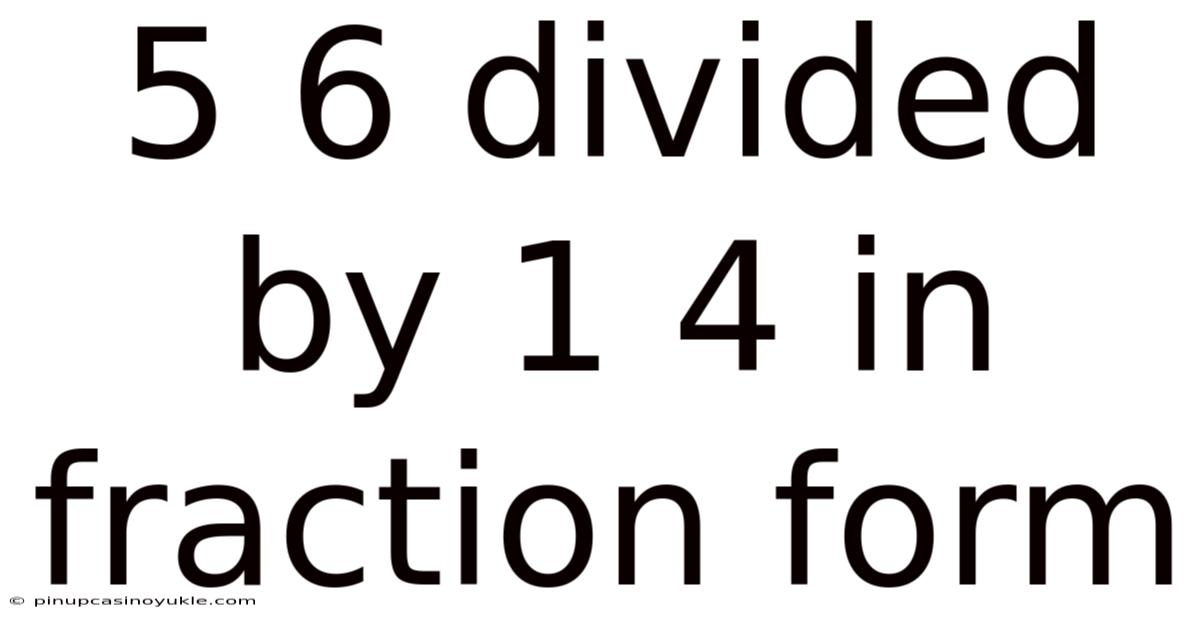
Table of Contents
Unlocking the Secrets of Fraction Division: Solving 5/6 Divided by 1/4
Fraction division, often perceived as a daunting task, is actually quite straightforward once you grasp the underlying principles. This article will demystify the process, specifically focusing on solving the problem of 5/6 divided by 1/4 in fraction form. We'll break down the steps, explore the reasoning behind them, and equip you with the knowledge to confidently tackle any fraction division problem.
Understanding Fractions: A Quick Recap
Before diving into the division process, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two key components:
- Numerator: The top number, indicating how many parts of the whole we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 5/6, 5 is the numerator, and 6 is the denominator. This means we have 5 parts out of a whole that has been divided into 6 equal parts.
The Division Dilemma: Conceptualizing Fraction Division
Division, in general, asks the question: "How many times does one number fit into another?" When dealing with fractions, this question becomes a bit more nuanced. Dividing 5/6 by 1/4 asks: "How many times does 1/4 fit into 5/6?"
Visualizing this can be helpful. Imagine you have 5/6 of a pizza. You want to know how many slices of 1/4 pizza you can get from that 5/6 portion. This is what fraction division helps us determine.
The Key to Success: "Keep, Change, Flip" (KCF)
The most common and effective method for dividing fractions is often referred to as the "Keep, Change, Flip" method, or KCF for short. Let's break down what each part of this mnemonic means:
- Keep: Keep the first fraction exactly as it is. In our case, we keep 5/6.
- Change: Change the division sign (÷) to a multiplication sign (×). This is a crucial step.
- Flip: Flip the second fraction (the divisor) by swapping its numerator and denominator. This means 1/4 becomes 4/1. This is also known as finding the reciprocal of the fraction.
Therefore, the problem 5/6 ÷ 1/4 transforms into 5/6 × 4/1.
Performing the Multiplication: Numerator Times Numerator, Denominator Times Denominator
Now that we've transformed the division problem into a multiplication problem, the process becomes much simpler. To multiply fractions, we follow a straightforward rule:
- Multiply the numerators together.
- Multiply the denominators together.
In our case:
- 5 × 4 = 20
- 6 × 1 = 6
This gives us the fraction 20/6.
Simplifying the Fraction: Finding the Greatest Common Factor (GCF)
The fraction 20/6 is a valid answer, but it's not in its simplest form. Simplifying a fraction means reducing it to its lowest terms, where the numerator and denominator have no common factors other than 1. To do this, we need to find the Greatest Common Factor (GCF) of 20 and 6.
The factors of 20 are: 1, 2, 4, 5, 10, and 20.
The factors of 6 are: 1, 2, 3, and 6.
The greatest common factor of 20 and 6 is 2.
Now, we divide both the numerator and the denominator by the GCF:
- 20 ÷ 2 = 10
- 6 ÷ 2 = 3
This gives us the simplified fraction 10/3.
Converting to a Mixed Number (Optional): Understanding the Value
While 10/3 is the simplest improper fraction (where the numerator is greater than the denominator), it can be helpful to convert it to a mixed number to better understand its value. A mixed number consists of a whole number and a proper fraction.
To convert 10/3 to a mixed number, we perform the following steps:
- Divide the numerator (10) by the denominator (3). 10 ÷ 3 = 3 with a remainder of 1.
- The whole number part of the mixed number is the quotient (3).
- The numerator of the fractional part is the remainder (1).
- The denominator of the fractional part remains the same (3).
Therefore, 10/3 is equivalent to the mixed number 3 1/3.
This means that 1/4 fits into 5/6 a total of 3 and 1/3 times.
Why "Keep, Change, Flip" Works: The Underlying Principle
The "Keep, Change, Flip" method might seem like a mathematical trick, but it's based on a fundamental principle: dividing by a fraction is the same as multiplying by its reciprocal. Let's explore why this is true.
Remember that a reciprocal of a number is simply 1 divided by that number. For a fraction a/b, its reciprocal is b/a. Multiplying a number by its reciprocal always results in 1. For example, (1/4) * (4/1) = 1.
Dividing by a number is the inverse operation of multiplying by that number. Since dividing by a fraction is difficult to conceptualize directly, we can use the inverse operation (multiplication) and the reciprocal of the divisor to achieve the same result.
Think of it this way: instead of asking "How many times does 1/4 fit into 5/6?", we're essentially asking "What number multiplied by 1/4 equals 5/6?". By multiplying 5/6 by the reciprocal of 1/4 (which is 4/1), we're finding that number.
Real-World Applications: Where Fraction Division Matters
Fraction division might seem like an abstract concept, but it has numerous practical applications in everyday life. Here are a few examples:
- Cooking and Baking: Recipes often involve fractions. If you want to scale a recipe up or down, you might need to divide fractions to adjust the ingredient quantities. For example, if a recipe calls for 1/2 cup of flour and you want to make half the recipe, you would divide 1/2 by 2 (which is the same as multiplying by 1/2), resulting in 1/4 cup of flour.
- Construction and Measurement: In construction, measurements are often expressed as fractions. Dividing fractions can be necessary for calculating the number of pieces needed for a project or determining the dimensions of a particular component.
- Sharing and Distribution: Imagine you have 5/6 of a cake and want to share it equally among 4 friends. You would divide 5/6 by 4 (which is the same as multiplying by 1/4) to determine how much cake each friend receives.
- Time Management: If you have a task that takes 5/6 of an hour and you want to divide it into 4 equal segments, you would divide 5/6 by 4 to determine the duration of each segment.
These are just a few examples of how fraction division can be applied in real-world scenarios. Understanding this concept can empower you to solve practical problems more effectively.
Common Mistakes to Avoid: Ensuring Accuracy
While the "Keep, Change, Flip" method is relatively simple, it's easy to make mistakes if you're not careful. Here are some common pitfalls to avoid:
- Forgetting to Flip: The most common mistake is forgetting to flip the second fraction (the divisor). Remember that you must find the reciprocal of the divisor before multiplying.
- Flipping the Wrong Fraction: It's crucial to flip only the second fraction (the divisor), not the first fraction (the dividend).
- Changing the Operation Before Flipping: Make sure you flip the fraction before performing the multiplication. Don't multiply the fractions and then attempt to flip the result.
- Not Simplifying: Failing to simplify the resulting fraction can lead to unnecessarily large numbers and a less clear understanding of the answer. Always simplify the fraction to its lowest terms.
- Confusing Division with Multiplication: While "Keep, Change, Flip" transforms division into multiplication, it's important to remember that the original problem was a division problem. Don't lose sight of the underlying concept.
By being mindful of these common mistakes, you can significantly improve your accuracy when dividing fractions.
Practice Problems: Sharpening Your Skills
The best way to master fraction division is through practice. Here are a few practice problems to help you hone your skills:
- 2/3 ÷ 1/2
- 7/8 ÷ 3/4
- 4/5 ÷ 2/3
- 1/2 ÷ 5/8
- 9/10 ÷ 3/5
Try solving these problems on your own, using the "Keep, Change, Flip" method. Check your answers against a calculator or online resource to ensure accuracy. The more you practice, the more comfortable and confident you'll become with fraction division.
Beyond the Basics: Exploring More Complex Scenarios
While we've focused on dividing simple fractions, the same principles apply to more complex scenarios, such as dividing mixed numbers or complex fractions.
- Dividing Mixed Numbers: To divide mixed numbers, first convert them to improper fractions. Then, proceed with the "Keep, Change, Flip" method as usual.
- Dividing Complex Fractions: A complex fraction is a fraction where the numerator or denominator (or both) contain fractions themselves. To divide a complex fraction, simplify the numerator and denominator separately, then divide the resulting fractions using the "Keep, Change, Flip" method.
These more complex scenarios might require a bit more effort, but the underlying principles remain the same.
The Importance of a Strong Foundation: Building on Fundamentals
Understanding fraction division is not just about memorizing a set of rules. It's about building a strong foundation in fundamental mathematical concepts. A solid understanding of fractions, reciprocals, and the relationship between multiplication and division is essential for success in more advanced mathematics.
By mastering these fundamentals, you'll be well-equipped to tackle more complex problems and gain a deeper appreciation for the beauty and power of mathematics.
Conclusion: Embracing the Power of Fractions
Fraction division might have seemed intimidating at first, but hopefully, this article has demystified the process and equipped you with the knowledge and skills to confidently solve problems like 5/6 divided by 1/4. By understanding the "Keep, Change, Flip" method, recognizing the underlying principles, and practicing regularly, you can master this essential mathematical concept and unlock its many real-world applications. So, embrace the power of fractions and continue exploring the fascinating world of mathematics! The answer to 5/6 divided by 1/4 is 10/3 or 3 1/3.
Latest Posts
Latest Posts
-
Que Es Una Reaccion En Quimica
Nov 26, 2025
-
How To Determine The Theme Of A Story
Nov 26, 2025
-
What Do The Parentheses In Math Mean
Nov 26, 2025
-
Does Electronegativity Increase From Left To Right
Nov 26, 2025
-
What Is The Measure Of Arc Ac
Nov 26, 2025
Related Post
Thank you for visiting our website which covers about 5 6 Divided By 1 4 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.