5 6 Divided By 1 12
pinupcasinoyukle
Nov 25, 2025 · 10 min read
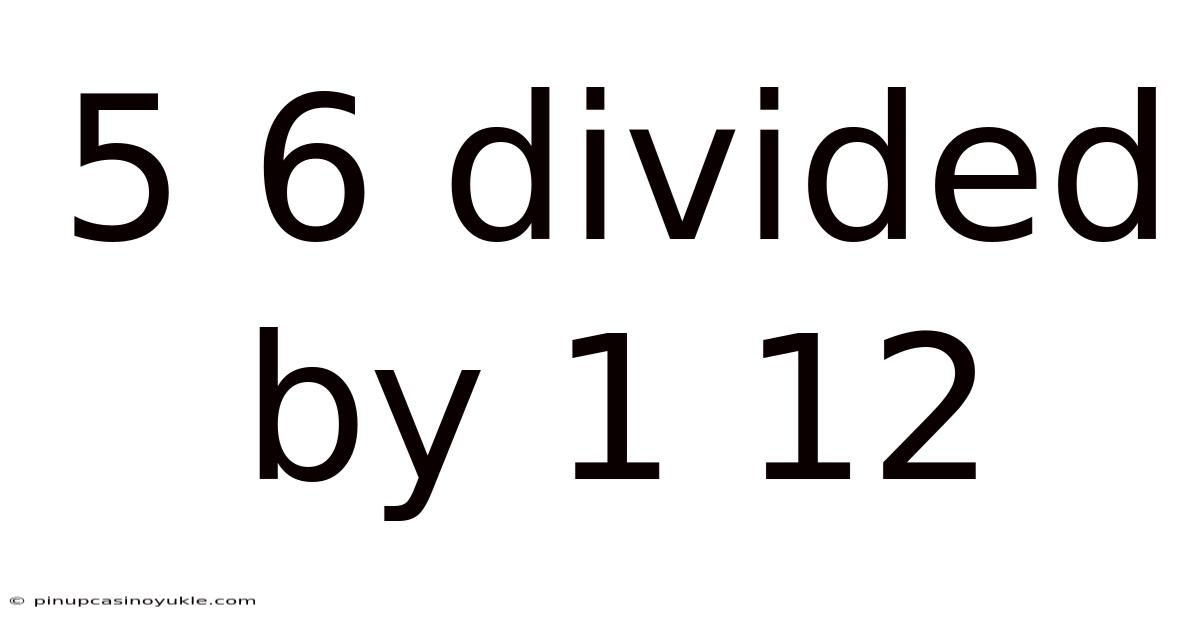
Table of Contents
Unraveling the Division: 5/6 Divided by 1/12
The seemingly simple mathematical operation of dividing 5/6 by 1/12 holds within it the key to understanding fractions and their interactions. Beyond just crunching numbers, this calculation reveals the underlying principles of division and how it applies to fractional quantities. This article will guide you through the process, providing a step-by-step explanation, exploring the conceptual reasoning, and addressing common questions that arise.
A Foundation in Fractions
Before diving into the division problem, let's solidify our understanding of fractions themselves. A fraction represents a part of a whole. It consists of two parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For instance, the fraction 5/6 signifies that we have 5 parts out of a total of 6 equal parts. Similarly, 1/12 represents 1 part out of a total of 12 equal parts.
The Division Dilemma: 5/6 ÷ 1/12
Now, let's confront the core question: what does it mean to divide 5/6 by 1/12? Conceptually, we're asking: "How many times does 1/12 fit into 5/6?" Alternatively, we can think of it as splitting 5/6 into groups the size of 1/12, and determining how many such groups we can make.
Directly dividing fractions can be tricky. Thankfully, we have a handy rule: dividing by a fraction is the same as multiplying by its reciprocal. This is the cornerstone of solving this problem.
Step-by-Step Solution: From Division to Multiplication
Let's break down the process into clear, manageable steps:
1. Identify the Fractions:
We are given two fractions: 5/6 and 1/12. The operation is division: 5/6 ÷ 1/12.
2. Find the Reciprocal of the Divisor:
The divisor is the fraction we are dividing by, which in this case is 1/12. The reciprocal of a fraction is obtained by flipping the numerator and denominator. Therefore, the reciprocal of 1/12 is 12/1 (or simply 12).
3. Change Division to Multiplication:
Replace the division sign (÷) with a multiplication sign (×). Now our problem becomes: 5/6 × 12/1.
4. Multiply the Numerators:
Multiply the numerators of the two fractions: 5 × 12 = 60.
5. Multiply the Denominators:
Multiply the denominators of the two fractions: 6 × 1 = 6.
6. Simplify the Resulting Fraction:
We now have the fraction 60/6. To simplify, we need to find the greatest common divisor (GCD) of the numerator and denominator. In this case, the GCD of 60 and 6 is 6.
Divide both the numerator and denominator by 6:
- 60 ÷ 6 = 10
- 6 ÷ 6 = 1
Therefore, the simplified fraction is 10/1, which is equal to 10.
Final Answer: 5/6 ÷ 1/12 = 10
The "Why" Behind the Flip: A Conceptual Explanation
The rule "dividing by a fraction is the same as multiplying by its reciprocal" can seem like a magic trick if we don't understand its underlying logic. Here's a breakdown to illuminate the concept:
Imagine you have a pizza that's 5/6 of a whole pizza. You want to divide this pizza into slices that are each 1/12 of a whole pizza. How many of these 1/12 slices can you get from your 5/6 of a pizza?
-
Thinking in Twelfths: First, let's convert 5/6 into an equivalent fraction with a denominator of 12. To do this, we multiply both the numerator and denominator of 5/6 by 2:
5/6 = (5 × 2) / (6 × 2) = 10/12
This means that 5/6 of the pizza is equivalent to 10/12 of the pizza.
-
Direct Comparison: Now we're asking: "How many 1/12 slices are there in 10/12 of a pizza?" The answer is clearly 10.
-
The Reciprocal Connection: Notice that we essentially multiplied 5/6 by 12 (which is the reciprocal of 1/12) to get our answer of 10. This is because multiplying by the reciprocal allows us to directly compare the fractional amounts in terms of a common unit (in this case, twelfths).
Another way to visualize this is to think of division as the inverse operation of multiplication. If a ÷ b = c, then c × b = a.
In our case, if 5/6 ÷ 1/12 = x, then x × 1/12 = 5/6. To find x, we need to isolate it. We can do this by multiplying both sides of the equation by the reciprocal of 1/12, which is 12:
(x × 1/12) × 12 = 5/6 × 12
x = 5/6 × 12
This demonstrates why dividing by a fraction is equivalent to multiplying by its reciprocal.
Real-World Applications of Dividing Fractions
Understanding how to divide fractions isn't just an abstract mathematical exercise. It has practical applications in various real-world scenarios:
-
Cooking and Baking: Recipes often involve scaling ingredients up or down. If you need to halve a recipe that calls for 5/6 cup of flour, you would divide 5/6 by 2 (or multiply by 1/2).
-
Construction and Measurement: When working with lumber or other materials, you might need to divide lengths or areas expressed as fractions. For example, if you have a board that is 5/6 of a meter long and you need to cut it into pieces that are 1/12 of a meter long, you would divide 5/6 by 1/12 to determine how many pieces you can get.
-
Time Management: If you have 5/6 of an hour to complete a task and you want to divide that time into 1/12-hour intervals, you would divide 5/6 by 1/12 to determine how many intervals you have.
-
Sharing and Distribution: Imagine you have 5/6 of a pizza to share equally among a certain number of people. If each person receives 1/12 of a whole pizza, you'd divide 5/6 by 1/12 to find out how many people can share the pizza.
These examples highlight the relevance of fraction division in everyday tasks and professional fields.
Common Mistakes and How to Avoid Them
While the process of dividing fractions is relatively straightforward, certain common errors can lead to incorrect answers. Being aware of these pitfalls can help you avoid them:
-
Forgetting to Flip the Divisor: The most frequent mistake is forgetting to take the reciprocal of the divisor before multiplying. Always remember to flip the second fraction (the one you are dividing by) before changing the division sign to multiplication.
-
Flipping the Wrong Fraction: Another common error is flipping the dividend (the fraction being divided) instead of the divisor. Make sure you identify the divisor correctly and take its reciprocal.
-
Multiplying Numerator by Denominator: Some students mistakenly multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa. Remember to multiply numerators with numerators and denominators with denominators after taking the reciprocal.
-
Incorrect Simplification: Failing to simplify the final fraction can lead to a technically correct but unrefined answer. Always look for common factors between the numerator and denominator to reduce the fraction to its simplest form.
-
Misunderstanding the Concept: A lack of conceptual understanding can make it difficult to apply the rule correctly. Spend time visualizing what division of fractions means to solidify your grasp of the underlying principles.
Extending the Concept: Dividing Mixed Numbers
The principles of dividing fractions can also be applied to mixed numbers (numbers consisting of a whole number and a fraction, such as 2 1/4). However, there's an essential preliminary step:
1. Convert Mixed Numbers to Improper Fractions:
Before dividing, you must convert any mixed numbers into improper fractions. An improper fraction is one where the numerator is greater than or equal to the denominator.
To convert a mixed number to an improper fraction, follow these steps:
- Multiply the whole number by the denominator of the fraction.
- Add the result to the numerator of the fraction.
- Keep the same denominator.
For example, to convert 2 1/4 to an improper fraction:
- 2 × 4 = 8
- 8 + 1 = 9
- Therefore, 2 1/4 = 9/4
2. Proceed with Division as Usual:
Once all mixed numbers have been converted to improper fractions, you can proceed with the division process as described earlier: find the reciprocal of the divisor, change division to multiplication, multiply the numerators, multiply the denominators, and simplify.
Example:
Let's say we want to divide 3 1/2 by 1/4.
- Convert to Improper Fractions: 3 1/2 = (3 × 2 + 1) / 2 = 7/2
- Reciprocal of Divisor: The reciprocal of 1/4 is 4/1 (or 4).
- Change to Multiplication: 7/2 ÷ 1/4 becomes 7/2 × 4/1.
- Multiply Numerators: 7 × 4 = 28
- Multiply Denominators: 2 × 1 = 2
- Simplify: 28/2 = 14
Therefore, 3 1/2 ÷ 1/4 = 14.
Exploring More Complex Scenarios
While dividing 5/6 by 1/12 yields a whole number (10), it's important to remember that the result of dividing fractions can also be a fraction. The steps remain the same, but the final simplification may result in a fractional answer.
Example:
Let's divide 1/2 by 3/4.
- Reciprocal of Divisor: The reciprocal of 3/4 is 4/3.
- Change to Multiplication: 1/2 ÷ 3/4 becomes 1/2 × 4/3.
- Multiply Numerators: 1 × 4 = 4
- Multiply Denominators: 2 × 3 = 6
- Simplify: 4/6 = 2/3
Therefore, 1/2 ÷ 3/4 = 2/3.
The Beauty of Fractional Arithmetic
The division of fractions, while sometimes perceived as a challenging topic, unveils the elegance and interconnectedness of mathematical concepts. By grasping the fundamental principles, mastering the procedural steps, and understanding the real-world applications, you can unlock a deeper appreciation for the power and versatility of fractional arithmetic. This knowledge not only empowers you to solve mathematical problems but also enhances your ability to reason quantitatively in various aspects of life.
FAQ: Frequently Asked Questions
-
Why do we flip the second fraction when dividing? Flipping the second fraction (taking its reciprocal) allows us to change the division problem into a multiplication problem, which is easier to solve. It's based on the mathematical principle that dividing by a number is the same as multiplying by its inverse.
-
What if I have a negative fraction? The same rules apply. Remember that a negative divided by a positive is negative, and a negative divided by a negative is positive.
-
Can I use a calculator? Yes, you can use a calculator to divide fractions. However, understanding the underlying process is crucial for developing mathematical intuition and problem-solving skills.
-
What if the fractions have different denominators? The division process remains the same. The key is to flip the divisor and multiply. Finding a common denominator is not necessary for division, only for addition and subtraction.
-
Is dividing fractions the same as dividing whole numbers? While the concept of division is the same (splitting into equal groups), the process differs slightly due to the nature of fractions. Dividing by a fraction can actually result in a larger number than you started with, which can be counterintuitive.
Conclusion: Mastering the Art of Fractional Division
Dividing fractions, like 5/6 divided by 1/12, is more than just a mathematical exercise; it's a gateway to understanding the relationships between numbers and their parts. By understanding the concept of reciprocals and the logical basis behind the "flip and multiply" rule, you can confidently tackle any fraction division problem. Remember to practice regularly, visualize the process, and connect the concepts to real-world scenarios to solidify your understanding. With consistent effort, you can master the art of fractional division and unlock a world of mathematical possibilities.
Latest Posts
Latest Posts
-
What Is The Lub Dub Sound Of The Heart
Nov 25, 2025
-
How To Do Good On The Sat
Nov 25, 2025
-
White House Staff Ap Gov Definition
Nov 25, 2025
-
What Does The Slope Of A Vt Graph Represent
Nov 25, 2025
-
Formula For Surface Area Of A Cuboid
Nov 25, 2025
Related Post
Thank you for visiting our website which covers about 5 6 Divided By 1 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.