300 Hundredths Divided By 5 Hundredths
pinupcasinoyukle
Nov 25, 2025 · 8 min read
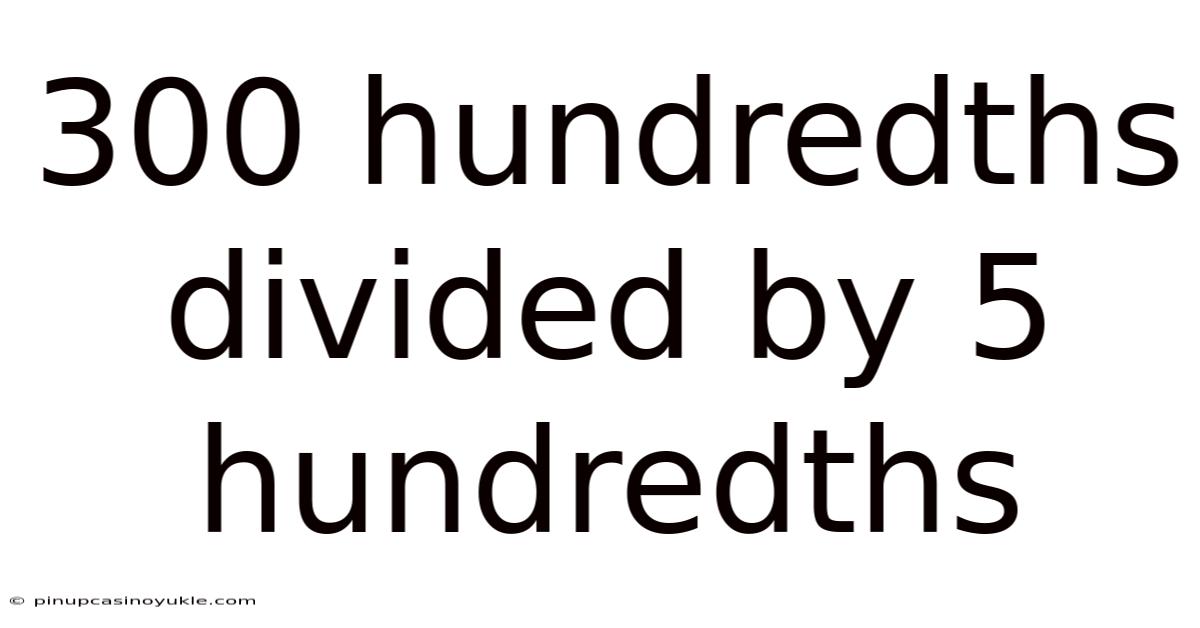
Table of Contents
Dividing 300 hundredths by 5 hundredths is a fundamental arithmetic operation that appears simple on the surface, yet understanding the underlying principles is crucial for grasping broader mathematical concepts. This article will provide a comprehensive exploration of this calculation, breaking down the process, explaining the concepts involved, offering practical examples, and addressing frequently asked questions.
Understanding Hundredths
Before diving into the division, it's essential to understand what hundredths represent. A hundredth is a fraction that represents one part out of one hundred, expressed as 1/100 or 0.01 in decimal form. Therefore, 300 hundredths mean 300 parts out of one hundred, or 300/100, and 5 hundredths mean 5 parts out of one hundred, or 5/100.
Converting Hundredths to Decimals
To work with hundredths effectively, converting them into decimal form is beneficial.
- 300 hundredths can be written as 300/100, which equals 3.00 or simply 3.
- 5 hundredths can be written as 5/100, which equals 0.05.
This conversion makes it easier to visualize and perform the division.
The Division Process: 300 Hundredths Divided by 5 Hundredths
The problem we need to solve is 300 hundredths divided by 5 hundredths. In mathematical terms, this can be written as:
300/100 ÷ 5/100
or
3 ÷ 0.05
Step-by-Step Calculation
Let's break down the division step by step:
-
Convert to Fractions: Express both numbers as fractions.
- 300 hundredths = 300/100
- 5 hundredths = 5/100
-
Write the Division Problem: Set up the division as a fraction. (300/100) / (5/100)
-
Invert and Multiply: To divide fractions, you invert the second fraction and multiply. (300/100) * (100/5)
-
Simplify: Cancel out the common factor of 100 in the numerator and the denominator. (300/1) * (1/5)
-
Multiply: Multiply the numerators and the denominators. 300/5
-
Divide: Perform the division. 300 ÷ 5 = 60
Therefore, 300 hundredths divided by 5 hundredths equals 60.
Alternative Approach: Using Decimals
Alternatively, you can perform the division using decimals:
-
Convert to Decimals:
- 300 hundredths = 3.00
- 5 hundredths = 0.05
-
Write the Division Problem: 3 ÷ 0.05
-
Remove the Decimal: To divide by a decimal, you can multiply both the dividend and the divisor by a power of 10 to remove the decimal from the divisor. In this case, multiply both by 100. (3 * 100) ÷ (0.05 * 100) 300 ÷ 5
-
Divide: 300 ÷ 5 = 60
Again, the result is 60.
Why Does This Work? The Underlying Mathematical Principles
The process of dividing 300 hundredths by 5 hundredths relies on fundamental mathematical principles related to fractions and decimals. Understanding these principles clarifies why the above steps lead to the correct answer.
Fractions and Division
Division by a fraction is equivalent to multiplication by its reciprocal (the inverted fraction). This principle is a cornerstone of arithmetic operations involving fractions. When we divide (300/100) by (5/100), we are essentially asking: "How many times does 5/100 fit into 300/100?"
The act of inverting and multiplying (i.e., multiplying by the reciprocal) provides a direct way to answer this question. The reciprocal of 5/100 is 100/5. Thus, the division problem becomes a multiplication problem:
(300/100) ÷ (5/100) = (300/100) * (100/5)
Decimals and Place Value
Decimals are another way of representing fractions with denominators that are powers of 10 (e.g., 10, 100, 1000). Each digit to the right of the decimal point represents a fraction with a denominator of 10, 100, 1000, and so on.
- The first digit after the decimal point represents tenths (1/10).
- The second digit represents hundredths (1/100).
- The third digit represents thousandths (1/1000), and so forth.
When we convert hundredths to decimals, we are simply expressing the fraction in a different notation. For example, 5 hundredths (5/100) is equivalent to 0.05.
Removing Decimals Through Multiplication
When dividing by a decimal, multiplying both the dividend and the divisor by a power of 10 is a technique used to simplify the problem. This technique is based on the principle that multiplying both the dividend and the divisor by the same number does not change the result of the division.
For example, consider the division problem 3 ÷ 0.05. Multiplying both numbers by 100 (which is 10^2) removes the decimal from the divisor:
(3 * 100) ÷ (0.05 * 100) = 300 ÷ 5
This transformation makes the division easier to perform because we are now dividing by a whole number.
Mathematical Equivalence
The key to understanding why these methods work is recognizing that they are mathematically equivalent. Whether we use fractions or decimals, the underlying mathematical relationships remain the same. Converting between fractions and decimals is a matter of notation, not a change in the inherent value of the numbers.
Practical Examples and Applications
To further illustrate the concept, let's consider some practical examples where dividing hundredths can be applied.
Example 1: Calculating Percentages
Percentages are essentially hundredths. If you want to determine what percentage 5 hundredths represents of 300 hundredths, you are essentially dividing 5 hundredths by 300 hundredths and then multiplying by 100 to express the result as a percentage.
(5/100) ÷ (300/100) = (5/100) * (100/300) = 5/300 = 1/60
To express this as a percentage:
(1/60) * 100 = 1.666...%
Example 2: Scaling Recipes
Imagine you have a recipe that calls for ingredients in hundredths of a unit. For instance, a recipe requires 5 hundredths of a kilogram of spice per serving, and you have 300 hundredths of a kilogram available. To find out how many servings you can make, you divide the total amount of spice by the amount required per serving:
300 hundredths ÷ 5 hundredths = 300/100 ÷ 5/100 = 60 servings
Example 3: Financial Calculations
In finance, interest rates and returns are often expressed in hundredths (percentage points). If you are comparing two investment options, where one yields a 300 hundredths return and the other yields a 5 hundredths return, you can determine how many times greater the first return is by dividing:
300 hundredths ÷ 5 hundredths = 60
This tells you that the first investment option yields 60 times the return of the second option.
Example 4: Measurement Conversions
In measurement, you might need to convert units expressed in hundredths. For example, if you have 300 hundredths of a meter and you want to know how many lengths of 5 hundredths of a meter you can measure, you would divide:
300 hundredths ÷ 5 hundredths = 60
This means you can measure 60 lengths of 5 hundredths of a meter.
Common Mistakes to Avoid
When performing division with hundredths, several common mistakes can lead to incorrect answers. Being aware of these pitfalls can help ensure accuracy.
Misunderstanding Decimal Placement
A frequent mistake is misplacing the decimal point when converting hundredths to decimals or when performing the division. For example, incorrectly converting 5 hundredths to 0.5 instead of 0.05 will lead to a wrong answer.
- Correct: 5 hundredths = 0.05
- Incorrect: 5 hundredths = 0.5
Incorrectly Inverting Fractions
When dividing fractions, it is crucial to invert the correct fraction (the divisor). Inverting the dividend instead will result in an incorrect answer.
- Correct: (300/100) ÷ (5/100) = (300/100) * (100/5)
- Incorrect: (300/100) ÷ (5/100) = (100/300) * (5/100)
Forgetting to Multiply Both Numbers
When removing decimals by multiplying, remember to multiply both the dividend and the divisor by the same power of 10. Multiplying only one of the numbers will change the problem and lead to an incorrect result.
- Correct: 3 ÷ 0.05 = (3 * 100) ÷ (0.05 * 100) = 300 ÷ 5
- Incorrect: 3 ÷ 0.05 = (3 * 100) ÷ 0.05 = 300 ÷ 0.05
Overlooking Simplification
Failing to simplify fractions before multiplying can make the calculation more complex. Simplifying by canceling common factors reduces the numbers and makes the division easier to manage.
- Correct: (300/100) * (100/5) = (300/1) * (1/5) = 300/5
- Less Efficient: (300/100) * (100/5) = 30000/500 = 300/5
Frequently Asked Questions (FAQ)
Q1: What is a hundredth?
A hundredth is one part out of one hundred, represented as 1/100 in fraction form or 0.01 in decimal form.
Q2: How do you convert hundredths to decimals?
To convert hundredths to decimals, divide the number of hundredths by 100. For example, 300 hundredths is 300/100 = 3.00, and 5 hundredths is 5/100 = 0.05.
Q3: Why do you invert and multiply when dividing fractions?
Dividing by a fraction is the same as multiplying by its reciprocal. This is because division is the inverse operation of multiplication.
Q4: Can you use a calculator to divide hundredths?
Yes, you can use a calculator. Enter the numbers as decimals (e.g., 3 ÷ 0.05) to get the result.
Q5: What is the reciprocal of 5/100?
The reciprocal of 5/100 is 100/5. To find the reciprocal, you simply switch the numerator and the denominator.
Q6: Why does multiplying both the dividend and divisor by 100 work?
Multiplying both the dividend and divisor by the same number does not change the value of the division because it is equivalent to multiplying the entire fraction by 1 (e.g., 100/100).
Q7: Are percentages related to hundredths?
Yes, percentages are directly related to hundredths. A percentage is a ratio expressed as a fraction of 100. Therefore, 1% is equal to 1/100 or 0.01.
Conclusion
Dividing 300 hundredths by 5 hundredths, whether approached through fractions or decimals, results in 60. This seemingly simple calculation underscores fundamental principles of arithmetic, including fraction division, decimal notation, and the importance of mathematical equivalence. By understanding these concepts and avoiding common pitfalls, one can confidently perform similar calculations in various practical contexts, from scaling recipes to financial analyses.
Latest Posts
Latest Posts
-
How To Solve Inequalities With Two Signs
Nov 25, 2025
-
Mean And Standard Deviation Of Binomial Distribution
Nov 25, 2025
-
Taj Mahal Ap World History Definition
Nov 25, 2025
-
How To Determine The Angle A Tangent Line Is Pointing
Nov 25, 2025
-
Work Done By Frictional Force Formula
Nov 25, 2025
Related Post
Thank you for visiting our website which covers about 300 Hundredths Divided By 5 Hundredths . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.