3 Is What Percent Of 15
pinupcasinoyukle
Nov 28, 2025 · 7 min read
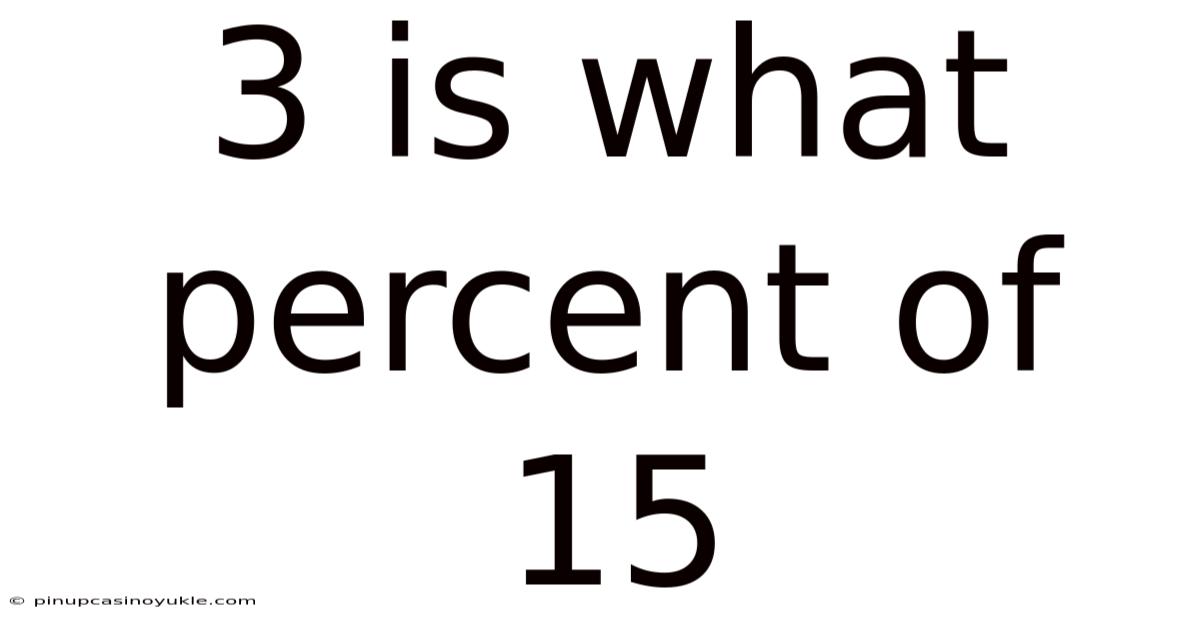
Table of Contents
Calculating percentages is a fundamental skill applicable in various real-life scenarios, from figuring out discounts while shopping to understanding statistical data. When faced with the question "3 is what percent of 15," it's essential to approach it with a clear, step-by-step methodology to arrive at the correct answer.
Understanding the Basics of Percentages
Before diving into the specific calculation, let's briefly review what percentages represent. The term "percent" comes from the Latin per centum, meaning "out of one hundred." A percentage is a way to express a number as a fraction of 100. Essentially, it tells you how many parts out of 100 a particular value represents.
For instance, if something is 50 percent, it means it constitutes 50 out of 100 parts, or half of the whole. Percentages are versatile and can be used to express ratios, changes, and distributions in an easily understandable format.
Setting Up the Problem: "3 is What Percent of 15?"
To solve "3 is what percent of 15," we need to determine what proportion 3 holds in relation to 15, expressed as a percentage. This involves identifying the part, the whole, and then calculating the percentage.
- Part: This is the number we want to express as a percentage of another number. In this case, the part is 3.
- Whole: This is the total or the reference number to which we compare the part. Here, the whole is 15.
- Percentage: This is the value we want to find, representing the part as a fraction of 100 of the whole.
The question can be rephrased as: "What percentage of 15 equals 3?"
Step-by-Step Calculation
Step 1: Forming the Fraction
The first step is to express the relationship between the part and the whole as a fraction. The part (3) becomes the numerator, and the whole (15) becomes the denominator. This gives us the fraction:
3 / 15
Step 2: Simplifying the Fraction (Optional but Recommended)
Simplifying the fraction makes the subsequent calculations easier. The fraction 3 / 15 can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 3.
3 ÷ 3 = 1
15 ÷ 3 = 5
So, the simplified fraction is:
1 / 5
Step 3: Converting the Fraction to a Decimal
To convert a fraction to a decimal, divide the numerator by the denominator:
1 ÷ 5 = 0.2
Alternatively, if you started with the original fraction 3 / 15:
3 ÷ 15 = 0.2
In either case, the decimal equivalent of the fraction is 0.2.
Step 4: Converting the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100:
0.2 × 100 = 20
This gives us the percentage.
Step 5: Stating the Answer
Therefore, 3 is 20% of 15.
Alternative Method: Using the Percentage Formula
Another way to solve this problem is by using the percentage formula directly. The formula is:
Percentage = (Part / Whole) × 100
Applying the Formula
- Part = 3
- Whole = 15
Plugging these values into the formula:
Percentage = (3 / 15) × 100
First, divide 3 by 15:
3 / 15 = 0.2
Then, multiply by 100:
0.2 × 100 = 20
So, the percentage is 20%.
Practical Examples and Applications
Understanding how to calculate percentages is useful in a variety of situations. Here are a few examples:
Example 1: Calculating Discounts
Suppose an item originally priced at $15 is on sale for $3 off. To find the discount percentage:
- Discount amount (Part) = $3
- Original price (Whole) = $15
Using the formula:
Percentage = (3 / 15) × 100 = 20%
The discount is 20%.
Example 2: Exam Scores
If a student scores 3 out of 15 questions correctly on a quiz, the percentage score is:
- Correct answers (Part) = 3
- Total questions (Whole) = 15
Percentage = (3 / 15) × 100 = 20%
The student scored 20% on the quiz.
Example 3: Financial Investments
Suppose you invested $15 in a stock, and it increased by $3. To find the percentage increase:
- Increase amount (Part) = $3
- Original investment (Whole) = $15
Percentage = (3 / 15) × 100 = 20%
Your investment increased by 20%.
Common Mistakes to Avoid
When calculating percentages, several common mistakes can lead to incorrect results. Here are some pitfalls to avoid:
Mistake 1: Confusing the Part and the Whole
One of the most frequent errors is mixing up the part and the whole. Always ensure that the part (the value you're interested in expressing as a percentage) is in the numerator and the whole (the total or reference value) is in the denominator. For example, when calculating "3 is what percent of 15," make sure 3 is the numerator and 15 is the denominator.
Mistake 2: Forgetting to Multiply by 100
After dividing the part by the whole, it's crucial to multiply the result by 100 to convert the decimal to a percentage. Forgetting this step will leave you with a decimal value, not a percentage. For instance, 3 / 15 = 0.2, but the percentage is 0.2 × 100 = 20%.
Mistake 3: Incorrectly Simplifying Fractions
Simplifying fractions can make calculations easier, but it must be done correctly. Ensure that you divide both the numerator and the denominator by their greatest common divisor. If you simplify incorrectly, your final percentage will be inaccurate.
Mistake 4: Rounding Errors
When dealing with percentages that result in long decimals, rounding can introduce errors if not done carefully. It's best to keep as many decimal places as possible until the final step and then round to the desired precision.
Mistake 5: Not Understanding the Context
Percentages are always relative to a specific context. Misinterpreting the context can lead to incorrect calculations. For example, if you're calculating a percentage change, make sure you understand whether the change is an increase or a decrease and apply the appropriate formula.
Advanced Applications of Percentages
Beyond basic calculations, percentages are used in more complex scenarios, such as:
Percentage Change
Percentage change is used to describe the degree to which a quantity changes over time. The formula for percentage change is:
Percentage Change = ((New Value - Old Value) / Old Value) × 100
For example, if a stock's price increases from $15 to $18, the percentage change is:
Percentage Change = (($18 - $15) / $15) × 100 = (3 / 15) × 100 = 20%
Compound Interest
Compound interest involves calculating interest on the initial principal and the accumulated interest from previous periods. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (as a decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
For example, if you invest $1,000 at an annual interest rate of 5% compounded annually for 10 years:
A = 1000 (1 + 0.05/1)^(1*10) = 1000 (1.05)^10 ≈ $1,628.89
Statistical Analysis
Percentages are frequently used in statistical analysis to express data in a standardized format. For example, you might calculate the percentage of respondents who agree with a particular statement in a survey.
Tips for Improving Accuracy
To ensure accurate percentage calculations, consider the following tips:
- Double-Check Your Numbers: Always verify that you have the correct values for the part and the whole.
- Use a Calculator: When dealing with complex numbers, a calculator can help reduce the risk of calculation errors.
- Write Down Your Steps: Documenting each step of the calculation can help you identify and correct any mistakes.
- Practice Regularly: The more you practice calculating percentages, the more comfortable and accurate you will become.
Conclusion
Calculating percentages is a fundamental mathematical skill with wide-ranging applications in everyday life. Whether you're figuring out discounts, analyzing financial data, or understanding statistical reports, the ability to calculate percentages accurately is essential. By understanding the basic principles, following a step-by-step approach, and avoiding common mistakes, you can confidently tackle any percentage-related problem. Specifically, answering "3 is what percent of 15" involves expressing the relationship as a fraction, converting it to a decimal, and then multiplying by 100, resulting in 20%. This skill not only enhances your mathematical proficiency but also empowers you to make informed decisions in various aspects of life.
Latest Posts
Latest Posts
-
How Many Inch In A Yard
Nov 28, 2025
-
How Do You Find Partial Pressure
Nov 28, 2025
-
Where Is The Gupta Empire Located
Nov 28, 2025
-
How Can The Environment Affect An Organisms Traits
Nov 28, 2025
-
Why Was The Shays Rebellion Important
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about 3 Is What Percent Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.