3 Is What Percent Of 12
pinupcasinoyukle
Nov 18, 2025 · 10 min read
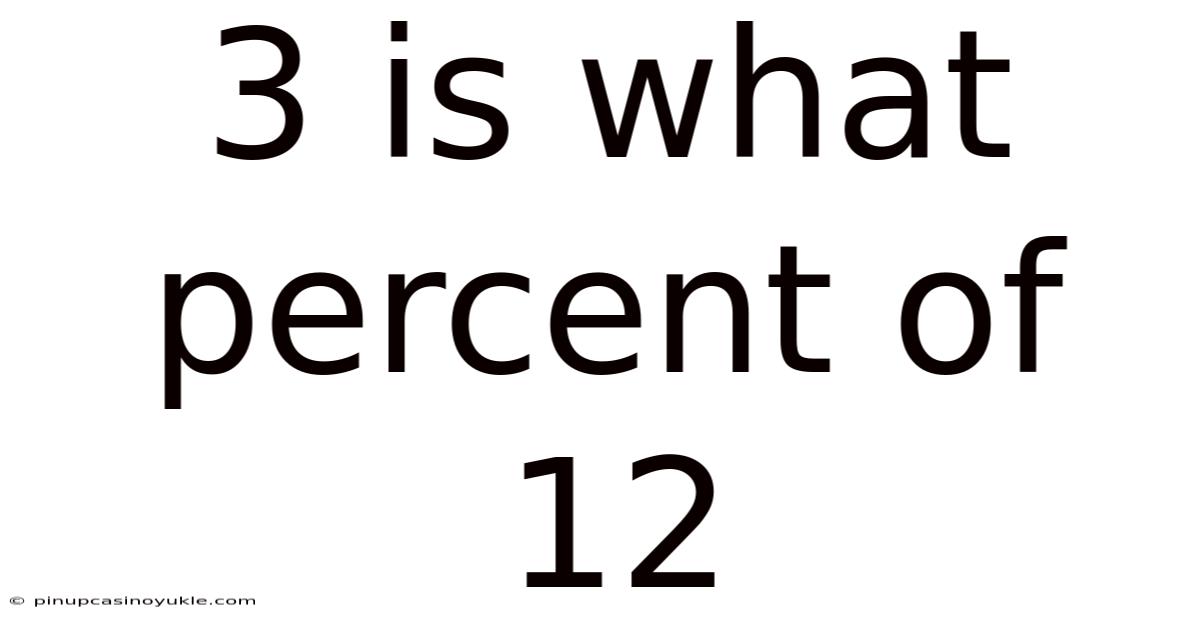
Table of Contents
Calculating percentages is a fundamental skill applicable in various facets of life, from figuring out discounts while shopping to understanding statistical data in professional settings. Mastering the basics of percentage calculation is crucial for both everyday tasks and advanced analytical processes. This article will delve into the specific calculation of "3 is what percent of 12," providing a comprehensive understanding and practical application of the concept.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. In essence, it tells you how much of a whole you have. The term "percent" comes from the Latin "per centum," meaning "out of one hundred." Therefore, when we say 50 percent, we mean 50 out of every 100.
To calculate a percentage, you typically divide the part by the whole and then multiply by 100. This gives you the percentage value. The formula can be represented as:
Percentage = (Part / Whole) * 100
In the context of our question, "3 is what percent of 12," we need to identify which number is the part and which is the whole.
- Part: The number we are comparing (in this case, 3).
- Whole: The total or reference number (in this case, 12).
Step-by-Step Calculation: 3 is What Percent of 12
To find what percentage 3 represents of 12, we will follow these steps:
- Identify the Part and the Whole: As mentioned earlier, 3 is the part and 12 is the whole.
- Apply the Formula: Use the percentage formula:
Percentage = (Part / Whole) * 100. - Substitute the Values: Plug in the numbers:
Percentage = (3 / 12) * 100. - Perform the Division: Divide 3 by 12:
3 / 12 = 0.25. - Multiply by 100: Multiply the result by 100 to convert it to a percentage:
0.25 * 100 = 25.
Therefore, 3 is 25% of 12.
Visual Representation
Visual aids can often enhance understanding, especially when dealing with mathematical concepts. Here are a few ways to visualize "3 is what percent of 12":
1. Pie Chart
Imagine a pie cut into 12 equal slices. If you take 3 of those slices, you would have one-quarter of the pie. A pie chart can visually represent this, showing that 3 slices out of 12 make up 25% of the whole pie.
2. Bar Graph
Consider a bar graph where the total height of the bar represents 12 units. If you shade the bar up to 3 units, the shaded portion would represent 25% of the total height.
3. Fraction Representation
Representing the problem as a fraction (3/12) and then simplifying it can provide an intuitive understanding. The fraction 3/12 simplifies to 1/4, and it’s well-known that 1/4 is equivalent to 25%.
Real-World Applications
Understanding how to calculate percentages is not just an academic exercise; it has numerous practical applications in daily life. Here are some examples:
1. Shopping Discounts
When shopping, you often encounter discounts expressed as percentages. For example, if an item originally priced at $12 is on sale for $3 off, you can calculate the discount percentage by finding what percent $3 is of $12. As we've already determined, $3 is 25% of $12, so the item is 25% off.
2. Test Scores
In academic settings, test scores are often expressed as percentages. If a student scores 3 out of 12 on a quiz, their score is 25%. This allows students and teachers to quickly understand performance relative to the total possible points.
3. Financial Planning
Percentages are crucial in financial planning. For example, if you save $3 out of every $12 you earn, you are saving 25% of your income. Understanding this can help you set and track savings goals.
4. Cooking and Baking
Recipes often use ratios and percentages to describe ingredient proportions. If a recipe calls for a certain amount of liquid relative to a solid ingredient, understanding percentages can help you adjust the recipe for different serving sizes.
5. Data Analysis
In data analysis, percentages are used to summarize and interpret data. For instance, if a survey of 12 people shows that 3 prefer a certain product, you can say that 25% of the respondents prefer that product.
Common Mistakes and How to Avoid Them
While the calculation itself is straightforward, there are common mistakes people make when calculating percentages. Here are a few and how to avoid them:
1. Confusing the Part and the Whole
One of the most common errors is misidentifying which number is the part and which is the whole. Always make sure that the part is the quantity you are comparing to the whole, which is the total or reference amount. In the question "3 is what percent of 12," 3 is the part and 12 is the whole.
2. Forgetting to Multiply by 100
After dividing the part by the whole, it's crucial to multiply the result by 100 to convert it to a percentage. Failing to do so will give you a decimal or fraction, not a percentage.
3. Rounding Errors
When dealing with percentages that result in long decimal values, rounding can introduce errors. Be mindful of the level of precision required for your application and round accordingly. For example, if you need to be accurate to the nearest tenth of a percent, round to one decimal place.
4. Misinterpreting the Question
Sometimes the wording of a percentage problem can be confusing. Always read the problem carefully to ensure you understand what is being asked. For example, "What is 3 percent of 12" is different from "3 is what percent of 12."
Advanced Applications of Percentage Calculations
Beyond basic calculations, percentages are used in more complex scenarios. Here are a few advanced applications:
1. Percentage Change
Percentage change is used to describe the relative change in a quantity over time. It is calculated using the formula:
Percentage Change = [(New Value - Old Value) / Old Value] * 100
For example, if a stock price increases from $12 to $15, the percentage change is:
Percentage Change = [(15 - 12) / 12] * 100 = (3 / 12) * 100 = 25%
This means the stock price increased by 25%.
2. Compound Interest
Compound interest involves earning interest on both the principal amount and the accumulated interest. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
A= the future value of the investment/loan, including interestP= the principal investment amount (the initial deposit or loan amount)r= the annual interest rate (as a decimal)n= the number of times that interest is compounded per yeart= the number of years the money is invested or borrowed for
Understanding percentages is essential for calculating and interpreting compound interest.
3. Statistical Analysis
In statistical analysis, percentages are used to describe the distribution of data, calculate confidence intervals, and perform hypothesis testing. For example, you might calculate the percentage of respondents who agree with a certain statement in a survey.
4. Business and Finance
Businesses use percentages extensively for financial reporting, sales analysis, and marketing campaigns. Understanding profit margins, revenue growth, and market share all rely on percentage calculations.
Practice Problems
To solidify your understanding, here are a few practice problems:
- What percentage is 5 of 20?
- What percentage is 15 of 50?
- What percentage is 8 of 32?
- What percentage is 25 of 100?
- What percentage is 7 of 28?
Answers:
- 25%
- 30%
- 25%
- 25%
- 25%
Tips for Mastering Percentage Calculations
- Understand the Terminology: Make sure you understand the meaning of "part," "whole," and "percent."
- Practice Regularly: The more you practice, the more comfortable you will become with percentage calculations.
- Use Real-World Examples: Apply percentage calculations to everyday situations to reinforce your understanding.
- Check Your Work: Always double-check your calculations to avoid errors.
- Use Tools and Resources: Utilize calculators, online tools, and educational resources to assist with complex calculations.
The Importance of Understanding Percentage in Education
Teaching and understanding percentages are vital in education for several reasons:
1. Foundational Mathematical Skill
Percentages build upon basic arithmetic skills such as division, multiplication, and fractions. Mastery of percentages is crucial for progressing to more advanced mathematical topics.
2. Real-World Relevance
As discussed earlier, percentages are used extensively in daily life, from shopping and cooking to financial planning and data analysis. Teaching percentages equips students with practical skills they can use throughout their lives.
3. Critical Thinking
Percentage problems often require critical thinking and problem-solving skills. Students must understand the context of the problem and apply the appropriate formulas and techniques to find the solution.
4. Preparation for Higher Education
Many fields of study, such as business, economics, science, and engineering, rely heavily on percentage calculations. A strong foundation in percentages prepares students for success in these disciplines.
5. Quantitative Literacy
Understanding percentages contributes to overall quantitative literacy, which is the ability to understand and use quantitative information to make informed decisions. Quantitative literacy is an essential skill for navigating the modern world.
Simplifying Complex Problems Using Percentages
Percentages can simplify complex problems by providing a common framework for comparison. Here are a few examples:
1. Comparing Proportions
When comparing proportions from different sample sizes, percentages allow for a standardized comparison. For example, if one survey finds that 30 out of 100 people prefer a certain product, and another survey finds that 60 out of 200 people prefer the same product, it's easier to compare the percentages (30% vs. 30%) than the raw numbers.
2. Analyzing Growth Rates
Percentages are often used to analyze growth rates in business and economics. For example, if a company's revenue increases from $1 million to $1.2 million, the growth rate can be expressed as a percentage:
Growth Rate = [(1.2 - 1) / 1] * 100 = 20%
This allows for easy comparison of growth rates across different companies or time periods.
3. Calculating Tax Rates
Tax rates are often expressed as percentages. Understanding how to calculate percentages is essential for determining the amount of tax owed on income, sales, or property.
4. Understanding Statistical Significance
In statistical analysis, percentages are used to determine the statistical significance of results. For example, if a clinical trial finds that a new drug is effective in 95% of patients, this percentage helps determine the drug's overall effectiveness and safety.
Advanced Techniques: Percentage Increase and Decrease
Understanding percentage increase and decrease is a crucial aspect of percentage calculations. These concepts are widely used in finance, economics, and everyday life.
1. Percentage Increase
Percentage increase is used to describe the relative increase in a quantity. The formula for percentage increase is:
Percentage Increase = [(New Value - Old Value) / Old Value] * 100
For example, if a product's price increases from $20 to $25, the percentage increase is:
Percentage Increase = [(25 - 20) / 20] * 100 = (5 / 20) * 100 = 25%
This means the product's price increased by 25%.
2. Percentage Decrease
Percentage decrease is used to describe the relative decrease in a quantity. The formula for percentage decrease is:
Percentage Decrease = [(Old Value - New Value) / Old Value] * 100
For example, if a product's price decreases from $20 to $15, the percentage decrease is:
Percentage Decrease = [(20 - 15) / 20] * 100 = (5 / 20) * 100 = 25%
This means the product's price decreased by 25%.
Conclusion
Calculating percentages is a fundamental skill with broad applications in various aspects of life. Understanding the basic formula Percentage = (Part / Whole) * 100 is the key to solving percentage problems. In the case of "3 is what percent of 12," the answer is 25%. By mastering this basic calculation and understanding the common mistakes to avoid, you can confidently apply percentages in real-world scenarios, from shopping discounts to financial planning and data analysis. Consistent practice and a clear understanding of the underlying concepts will solidify your skills and enable you to tackle more complex percentage-related problems.
Latest Posts
Latest Posts
-
How To Find The Center Of A Triangle
Nov 18, 2025
-
What Is The Standard Equation Of A Circle
Nov 18, 2025
-
All About Me Worksheets For Preschoolers
Nov 18, 2025
-
What Are The Two Classes Of Pure Substances
Nov 18, 2025
-
The Sum Of The Interior Angles Of A Triangle Is
Nov 18, 2025
Related Post
Thank you for visiting our website which covers about 3 Is What Percent Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.