3 4 Divided By 1 1 2
pinupcasinoyukle
Nov 20, 2025 · 10 min read
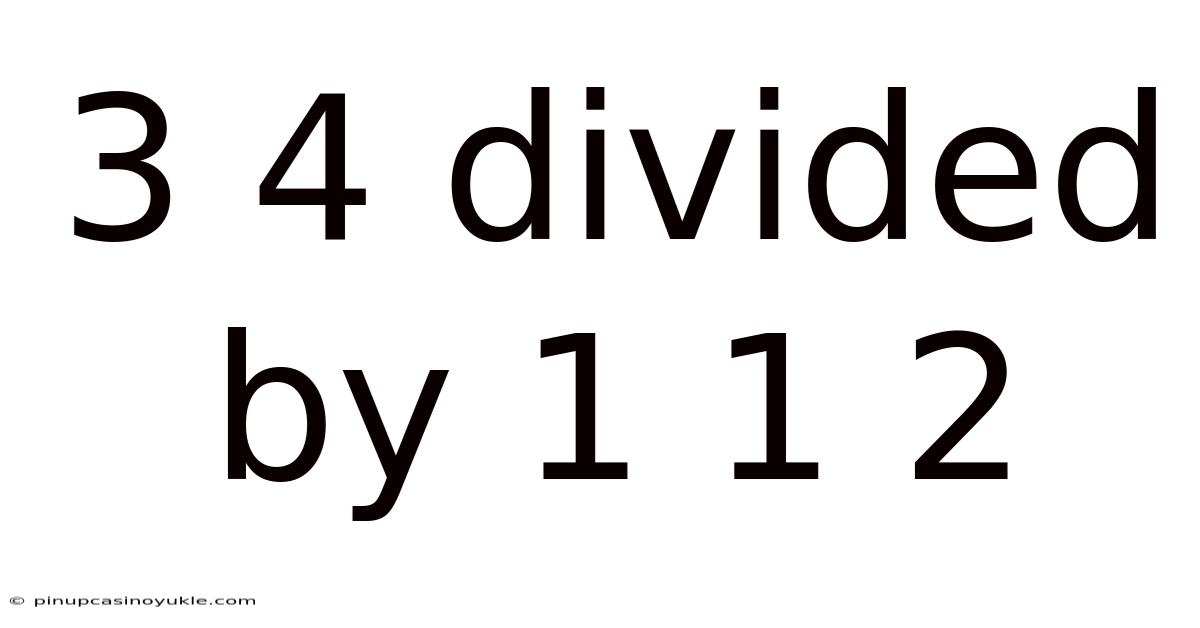
Table of Contents
Dividing fractions might seem daunting at first, but with the right approach and a clear understanding of the underlying principles, it becomes a straightforward and even intuitive process. This article will guide you through the steps to solve the problem 3 4 divided by 1 1 2, explaining each stage in detail and providing additional tips to help you master fraction division.
Understanding Fractions: A Quick Review
Before diving into the division itself, let's briefly recap what fractions represent and the different types of fractions.
- Definition: A fraction represents a part of a whole. It consists of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator.
- Types of Fractions:
- Proper Fraction: The numerator is smaller than the denominator (e.g., 1/2, 3/4, 5/8).
- Improper Fraction: The numerator is greater than or equal to the denominator (e.g., 4/3, 5/2, 7/7).
- Mixed Number: A whole number combined with a proper fraction (e.g., 1 1/2, 2 3/4, 5 1/4).
Understanding these basics is crucial for performing operations with fractions, including division.
Setting Up the Problem: 3/4 Divided by 1 1/2
Our problem is to divide 3/4 by 1 1/2. The first step is to convert any mixed numbers into improper fractions. In this case, we need to convert 1 1/2 into an improper fraction.
Converting a Mixed Number to an Improper Fraction:
To convert a mixed number like 1 1/2 to an improper fraction, follow these steps:
- Multiply the whole number (1) by the denominator of the fraction (2): 1 * 2 = 2.
- Add the result to the numerator of the fraction (1): 2 + 1 = 3.
- Place the result over the original denominator (2).
So, 1 1/2 is equal to 3/2.
Now our division problem looks like this: 3/4 ÷ 3/2.
The Key to Dividing Fractions: Multiplying by the Reciprocal
The fundamental rule for dividing fractions is to multiply by the reciprocal of the second fraction. The reciprocal of a fraction is obtained by swapping its numerator and denominator.
Finding the Reciprocal:
The reciprocal of 3/2 is 2/3. We simply flipped the numerator and the denominator.
Now, instead of dividing 3/4 by 3/2, we multiply 3/4 by 2/3:
3/4 ÷ 3/2 becomes 3/4 * 2/3
Performing the Multiplication
To multiply fractions, we multiply the numerators together and the denominators together.
Step-by-Step Multiplication:
- Multiply the numerators: 3 * 2 = 6
- Multiply the denominators: 4 * 3 = 12
So, 3/4 * 2/3 = 6/12.
Simplifying the Result: Reducing the Fraction
The fraction 6/12 can be simplified, or reduced, to its simplest form. This means finding the greatest common factor (GCF) of the numerator and the denominator and dividing both by that factor.
Finding the Greatest Common Factor (GCF):
The GCF of 6 and 12 is 6. This is the largest number that divides both 6 and 12 evenly.
Simplifying the Fraction:
Divide both the numerator and the denominator by 6:
- 6 ÷ 6 = 1
- 12 ÷ 6 = 2
Therefore, 6/12 simplifies to 1/2.
The Final Answer
So, 3/4 divided by 1 1/2 is equal to 1/2.
A Recap of the Steps
Let's summarize the steps we took to solve this problem:
- Convert Mixed Numbers to Improper Fractions: 1 1/2 became 3/2.
- Rewrite the Division as Multiplication by the Reciprocal: 3/4 ÷ 3/2 became 3/4 * 2/3.
- Multiply the Fractions: 3/4 * 2/3 = 6/12.
- Simplify the Result: 6/12 simplified to 1/2.
Why Does Dividing by a Fraction Involve Multiplying by the Reciprocal?
The concept of dividing by a fraction being equivalent to multiplying by its reciprocal might seem counterintuitive. To understand this, let's consider what division actually means.
Division as the Inverse of Multiplication:
Division is the inverse operation of multiplication. For example, 10 ÷ 2 = 5 because 5 * 2 = 10. In other words, division answers the question: "How many times does one number fit into another?"
When we divide by a fraction, we are asking how many times that fraction fits into the number being divided. For instance, if we want to divide 1 by 1/2, we are asking how many halves fit into 1. The answer is 2, because two halves make a whole. So, 1 ÷ 1/2 = 2.
Visualizing the Concept:
Imagine you have one pizza. If you divide it into halves, you get two slices (1/2 each). This is the same as saying 1 ÷ 1/2 = 2.
Now, let's look at this in terms of multiplying by the reciprocal. The reciprocal of 1/2 is 2/1, which is just 2. So, 1 * 2 = 2. This shows that dividing by 1/2 is the same as multiplying by 2.
Generalizing the Rule:
When we divide by a fraction a/b, we are essentially asking how many a/b pieces fit into a given number. Multiplying by the reciprocal b/a accomplishes the same thing.
Let's use a more complex example: 3/4 ÷ 3/2. We are asking how many 3/2 pieces fit into 3/4. Intuitively, we know that 3/2 is larger than 3/4, so the answer will be less than 1. In fact, 3/2 is twice as big as 3/4, so 3/4 is half of 3/2. Therefore, 3/4 ÷ 3/2 = 1/2.
Now, let's multiply by the reciprocal: 3/4 * 2/3 = 6/12, which simplifies to 1/2.
This demonstrates that multiplying by the reciprocal is a valid and effective method for dividing fractions because it aligns with the fundamental principles of division as the inverse of multiplication.
Common Mistakes to Avoid
When dividing fractions, it's easy to make mistakes. Here are some common pitfalls to watch out for:
- Forgetting to Convert Mixed Numbers: Always convert mixed numbers to improper fractions before performing any operations. Failing to do so will lead to incorrect results.
- Dividing Instead of Multiplying by the Reciprocal: The most common mistake is attempting to divide the numerators and denominators directly. Remember, dividing fractions requires multiplying by the reciprocal of the second fraction.
- Taking the Reciprocal of the Wrong Fraction: Make sure to take the reciprocal of the second fraction (the divisor), not the first fraction (the dividend).
- Forgetting to Simplify: Always simplify your final answer to its simplest form. This makes the answer easier to understand and work with in future calculations.
- Incorrectly Finding the GCF: When simplifying, ensure you find the greatest common factor. Using a smaller common factor will require further simplification.
By being aware of these common mistakes, you can avoid them and ensure accurate results when dividing fractions.
Practice Problems
To solidify your understanding of dividing fractions, try solving these practice problems:
- 2/5 ÷ 1/3
- 4/7 ÷ 2/5
- 1 1/4 ÷ 3/8
- 2 1/2 ÷ 1 1/3
- 5/6 ÷ 1 1/2
Answers:
- 6/5 or 1 1/5
- 10/7 or 1 3/7
- 10/3 or 3 1/3
- 15/8 or 1 7/8
- 5/9
Working through these problems will help you become more comfortable and confident in dividing fractions.
Real-World Applications of Dividing Fractions
Fractions and their division have numerous practical applications in everyday life. Here are a few examples:
- Cooking and Baking: Recipes often call for fractional amounts of ingredients. If you need to halve or double a recipe, you'll be dividing or multiplying fractions. For instance, if a recipe calls for 3/4 cup of flour, and you only want to make half the recipe, you would divide 3/4 by 2 (or multiply by 1/2), resulting in 3/8 cup of flour.
- Construction and Carpentry: When building or working with wood, precise measurements are crucial. Fractions are commonly used to measure lengths and distances. Dividing fractions can help you determine how many pieces of a certain length can be cut from a larger piece of material. For example, if you have a 10-foot board and need to cut pieces that are 2 1/2 feet long, you would divide 10 by 2 1/2 (or 5/2), which equals 4. This means you can cut four pieces of that length from the board.
- Time Management: Dividing tasks or activities into smaller, manageable fractions can help with time management. For instance, if you have 2 hours (120 minutes) to complete three tasks, you might divide the time equally among the tasks. If each task takes approximately the same amount of time, you would divide 120 minutes by 3, which equals 40 minutes per task. You could also express this as each task receiving 1/3 of the total time.
- Sharing and Distribution: Dividing fractions is useful when sharing or distributing items equally among a group of people. For example, if you have 3/4 of a pizza and want to share it equally among 3 people, you would divide 3/4 by 3, which equals 1/4. Each person would receive 1/4 of the pizza.
- Calculating Proportions and Ratios: Fractions are essential for calculating proportions and ratios in various fields, such as science, engineering, and finance. Dividing fractions can help you determine the relationship between different quantities. For instance, if you're mixing a solution that requires a ratio of 1 part chemical A to 2 1/2 parts water, you would use fractions to calculate the exact amounts needed.
These examples illustrate how understanding and being able to divide fractions is a valuable skill that can be applied in a wide range of practical situations.
Advanced Topics: Dividing Complex Fractions
While we've covered the basics of dividing fractions, it's worth briefly touching on more complex scenarios involving complex fractions. A complex fraction is a fraction where the numerator, the denominator, or both contain fractions themselves. For example:
(1/2) / (3/4) or (2 + 1/3) / (5/6)
Simplifying Complex Fractions:
To simplify complex fractions, the general approach is to:
- Simplify the Numerator and Denominator Separately: If the numerator or denominator contains multiple terms or operations, simplify them into a single fraction.
- Rewrite the Complex Fraction as a Division Problem: Treat the main fraction bar as a division symbol.
- Multiply by the Reciprocal: Multiply the numerator (the dividend) by the reciprocal of the denominator (the divisor).
- Simplify the Result: Simplify the resulting fraction to its simplest form.
Example:
Let's simplify the complex fraction (2 + 1/3) / (5/6):
-
Simplify the Numerator: 2 + 1/3 = 6/3 + 1/3 = 7/3
-
Rewrite as a Division Problem: (7/3) / (5/6)
-
Multiply by the Reciprocal: (7/3) * (6/5) = 42/15
-
Simplify the Result: 42/15 = 14/5 or 2 4/5
Therefore, (2 + 1/3) / (5/6) simplifies to 14/5 or 2 4/5.
Dealing with complex fractions may require additional steps, but the underlying principles of fraction division remain the same: convert to improper fractions, multiply by the reciprocal, and simplify.
Conclusion
Dividing fractions, though seemingly complex at first, is a manageable skill when broken down into simple steps. By converting mixed numbers to improper fractions, understanding the concept of reciprocals, and following the rule of multiplying by the reciprocal, you can confidently solve any fraction division problem. Remember to simplify your answers to their simplest form. Practice regularly, and you'll find that dividing fractions becomes second nature. The ability to work with fractions is a valuable skill that extends beyond the classroom and into various real-world applications, making it a worthwhile endeavor to master. Whether you're adjusting a recipe, measuring materials for a project, or managing your time, a solid understanding of fraction division will serve you well.
Latest Posts
Latest Posts
-
Is Ice More Or Less Dense Than Water
Nov 20, 2025
-
How To Know If Two Triangle Are Congruent
Nov 20, 2025
-
Work Is The Change In Kinetic Energy
Nov 20, 2025
-
For The Following Right Triangle Find The Side Length
Nov 20, 2025
-
Ap Bio Unit 4 Practice Questions
Nov 20, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Divided By 1 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.