3 + 3 X 3 - 3 + 3
pinupcasinoyukle
Nov 05, 2025 · 9 min read
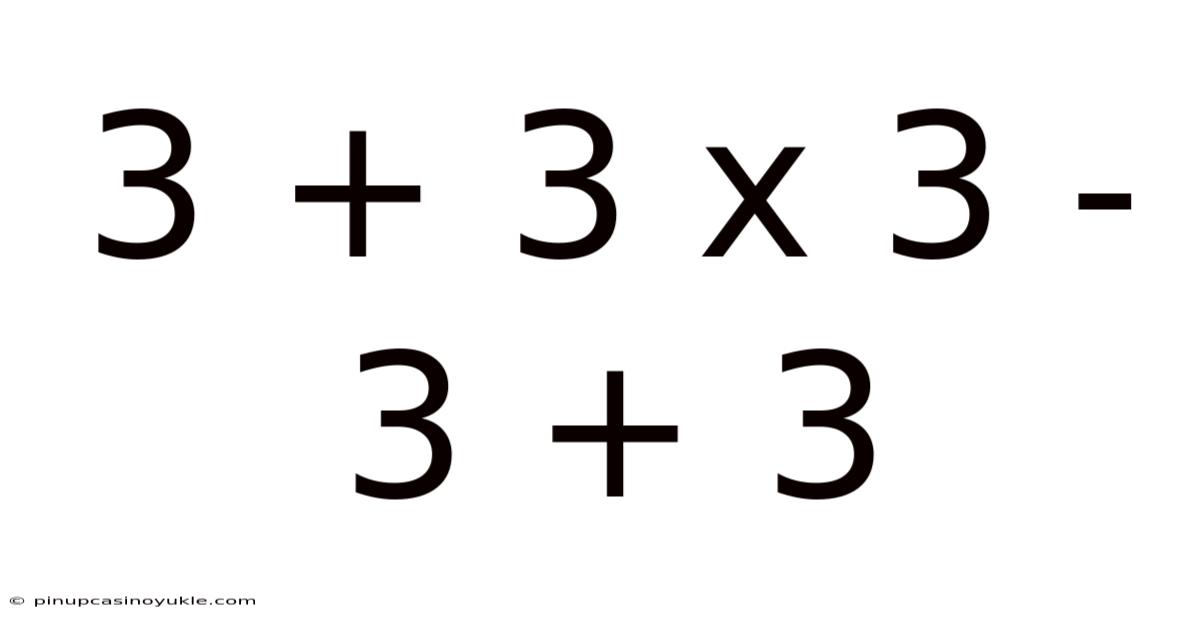
Table of Contents
Let's dive into the deceptively simple world of mathematical operations with the expression 3 + 3 x 3 - 3 + 3. While it might seem straightforward at first glance, a proper understanding of the order of operations is crucial to arrive at the correct answer. This article will comprehensively break down the calculation, explore the underlying principles, discuss common pitfalls, and provide a deeper understanding of how mathematical conventions govern even the simplest of equations.
The Order of Operations: A Foundation for Calculation
The key to solving any mathematical expression lies in following the established order of operations, often remembered by the acronyms PEMDAS or BODMAS:
- Parentheses / Brackets
- Exponents / Orders
- Multiplication and Division (from left to right)
- Addition and Subtraction (from left to right)
This order dictates the sequence in which operations should be performed to ensure a consistent and unambiguous result. Ignoring this order will almost certainly lead to an incorrect answer.
Step-by-Step Solution: Unraveling the Equation
Now, let's apply the order of operations to our expression: 3 + 3 x 3 - 3 + 3
-
Multiplication: According to PEMDAS/BODMAS, multiplication takes precedence over addition and subtraction. Therefore, we begin by multiplying 3 x 3:
3 + (3 x 3) - 3 + 3 = 3 + 9 - 3 + 3
-
Addition and Subtraction (from left to right): Now we perform addition and subtraction, working from left to right:
- 3 + 9 = 12 12 - 3 = 9 9 + 3 = 12
Therefore, the correct answer to the expression 3 + 3 x 3 - 3 + 3 is 12.
Why the Order Matters: Avoiding Ambiguity
The order of operations isn't an arbitrary rule; it's a fundamental convention that ensures everyone arrives at the same answer when evaluating a mathematical expression. Without it, the expression 3 + 3 x 3 - 3 + 3 could be interpreted in multiple ways, leading to different, incorrect results.
For instance, if we were to perform the operations from left to right without considering the order of operations, we would get:
- 3 + 3 = 6 6 x 3 = 18 18 - 3 = 15 15 + 3 = 18
This incorrect calculation yields an answer of 18, which significantly differs from the correct answer of 12. This highlights the importance of adhering to the established order to avoid ambiguity and ensure accurate results.
Common Mistakes and Misconceptions
Even with a basic understanding of the order of operations, it's easy to make mistakes. Here are some common pitfalls to watch out for:
- Treating all operations equally: A common error is to perform addition and subtraction before multiplication or division. Remember that multiplication and division always come first (from left to right), followed by addition and subtraction (from left to right).
- Ignoring the left-to-right rule: When faced with a series of additions and subtractions (or multiplications and divisions), remember to perform the operations from left to right. This ensures the correct sequence is followed.
- Overlooking parentheses: Parentheses (or brackets) always take the highest priority. Any operations within parentheses must be performed before anything outside of them. Our example doesn't contain parentheses, but it's important to remember this rule for more complex expressions.
- Calculator errors: Be mindful of how your calculator handles the order of operations. Some basic calculators may simply perform operations in the order they are entered, leading to incorrect results. Scientific calculators generally follow the correct order of operations.
Applying the Order of Operations in Real-World Scenarios
The order of operations isn't just a theoretical concept; it's essential for accurate calculations in various real-world applications, including:
- Programming: Programming languages rely heavily on the order of operations to execute code correctly. Incorrectly ordered calculations can lead to unexpected errors and bugs.
- Finance: Financial calculations, such as compound interest and investment returns, require precise adherence to the order of operations to ensure accurate results.
- Engineering: Engineers use mathematical models to design and analyze structures, circuits, and other systems. The order of operations is critical for ensuring the accuracy and reliability of these models.
- Data Analysis: When analyzing data, it's crucial to perform calculations correctly to draw meaningful conclusions. The order of operations plays a vital role in ensuring data integrity.
- Everyday life: Even in everyday situations, understanding the order of operations can be helpful. For example, when calculating the total cost of items with discounts and taxes, you need to apply the correct order to get the right price.
The Importance of Practice and Reinforcement
Mastering the order of operations requires consistent practice and reinforcement. Here are some tips for improving your understanding and accuracy:
- Work through practice problems: Solve a variety of expressions with different combinations of operations. This will help you internalize the rules and develop your problem-solving skills.
- Use online resources: Numerous websites and apps offer practice problems and tutorials on the order of operations. These resources can provide valuable support and feedback.
- Create your own problems: Challenge yourself by creating your own expressions and solving them. This will deepen your understanding of the concepts and improve your ability to apply them.
- Explain the concepts to others: Teaching the order of operations to someone else is a great way to solidify your own understanding. By explaining the rules and working through examples, you'll gain a deeper appreciation for the underlying principles.
- Pay attention to detail: Accuracy is crucial when working with mathematical expressions. Take your time, double-check your work, and be mindful of potential errors.
Beyond the Basics: Exploring More Complex Expressions
Once you have a solid grasp of the basic order of operations, you can move on to more complex expressions involving parentheses, exponents, and other advanced mathematical concepts. Here are some examples:
- (2 + 3) x 4 - 5: In this case, you would first solve the expression within the parentheses (2 + 3 = 5), then multiply by 4 (5 x 4 = 20), and finally subtract 5 (20 - 5 = 15).
- 2 + 3^2 x 4: Here, you would first calculate the exponent (3^2 = 9), then multiply by 4 (9 x 4 = 36), and finally add 2 (36 + 2 = 38).
- 10 / 2 + 3 x (4 - 1): In this expression, you would first solve the expression within the parentheses (4 - 1 = 3), then perform the division (10 / 2 = 5), then the multiplication (3 x 3 = 9), and finally add the results (5 + 9 = 14).
By working through these types of problems, you can further refine your skills and develop a deeper understanding of how the order of operations applies to a wider range of mathematical expressions.
Order of Operations with Fractions and Decimals
The order of operations also applies to expressions involving fractions and decimals. Remember to treat fractions and decimals just like any other number and follow the same rules for prioritizing operations.
For example:
- (1/2 + 1/4) x 2: First, add the fractions inside the parentheses: 1/2 + 1/4 = 3/4. Then, multiply by 2: (3/4) x 2 = 3/2 or 1.5.
- 2.5 x 3 - 1.2 + 0.5: First, multiply 2.5 x 3 = 7.5. Then, subtract 1.2: 7.5 - 1.2 = 6.3. Finally, add 0.5: 6.3 + 0.5 = 6.8.
When dealing with fractions, it's often helpful to simplify them before performing other operations. Similarly, converting decimals to fractions (or vice versa) can sometimes make calculations easier.
Advanced Concepts: Beyond Basic Arithmetic
While the order of operations is often taught in the context of basic arithmetic, it's also essential for more advanced mathematical concepts, such as:
- Algebra: Algebraic expressions often involve variables and complex combinations of operations. The order of operations is crucial for simplifying and solving these expressions.
- Calculus: Calculus involves limits, derivatives, and integrals, all of which require a thorough understanding of the order of operations.
- Statistics: Statistical calculations often involve complex formulas and data analysis techniques. The order of operations is essential for ensuring the accuracy of these calculations.
- Linear Algebra: Operations with matrices and vectors also rely on the correct order of operations.
By mastering the order of operations, you'll be well-prepared to tackle more advanced mathematical concepts and applications.
The Role of Technology: Calculators and Computers
While it's important to understand the underlying principles of the order of operations, technology can be a valuable tool for performing calculations quickly and accurately.
- Calculators: Scientific calculators are designed to follow the correct order of operations automatically. However, it's still important to understand how the calculator works and to double-check your work, especially for complex expressions.
- Computer software: Spreadsheet programs, programming languages, and other software tools can be used to perform complex calculations with ease. However, it's crucial to ensure that the software is configured to follow the correct order of operations and that you understand how to use the software effectively.
- Online calculators: Numerous online calculators are available that can perform complex calculations. However, it's important to choose a reputable calculator and to be aware of its limitations.
While technology can be helpful, it's important to remember that it's just a tool. A solid understanding of the order of operations is essential for using technology effectively and for interpreting the results correctly.
Mnemonics and Memory Aids
To help remember the order of operations, several mnemonics have been developed. The most common are:
- PEMDAS: Parentheses, Exponents, Multiplication and Division, Addition and Subtraction.
- BODMAS: Brackets, Orders, Division and Multiplication, Addition and Subtraction.
- Please Excuse My Dear Aunt Sally: Parentheses, Exponents, Multiplication and Division, Addition and Subtraction.
Choose the mnemonic that works best for you and use it to help you remember the order of operations.
Conclusion: Mastering the Fundamentals
In conclusion, the expression 3 + 3 x 3 - 3 + 3 serves as a simple yet powerful illustration of the importance of the order of operations in mathematics. By consistently applying the rules of PEMDAS or BODMAS, we arrive at the correct answer of 12. Understanding and adhering to these conventions not only prevents errors but also ensures clarity and consistency in mathematical communication and problem-solving. Mastering these fundamental principles opens the door to more complex mathematical concepts and real-world applications, making it a crucial skill for students, professionals, and anyone seeking to improve their analytical abilities. Therefore, practice, reinforcement, and a keen eye for detail are key to mastering the order of operations and unlocking the power of accurate calculation.
Latest Posts
Latest Posts
-
Rotating And Scaling Interpretation Of Dividing Complex Numbers
Nov 05, 2025
-
What Percent Is 25 Of 30
Nov 05, 2025
-
Government Power Comes From The Will Of The People
Nov 05, 2025
-
Do You Put Song Titles In Quotation Marks
Nov 05, 2025
-
Which Of The Following Function Types Exhibit The End Behavior
Nov 05, 2025
Related Post
Thank you for visiting our website which covers about 3 + 3 X 3 - 3 + 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.