20 Is What Percent Of 65
pinupcasinoyukle
Nov 18, 2025 · 9 min read
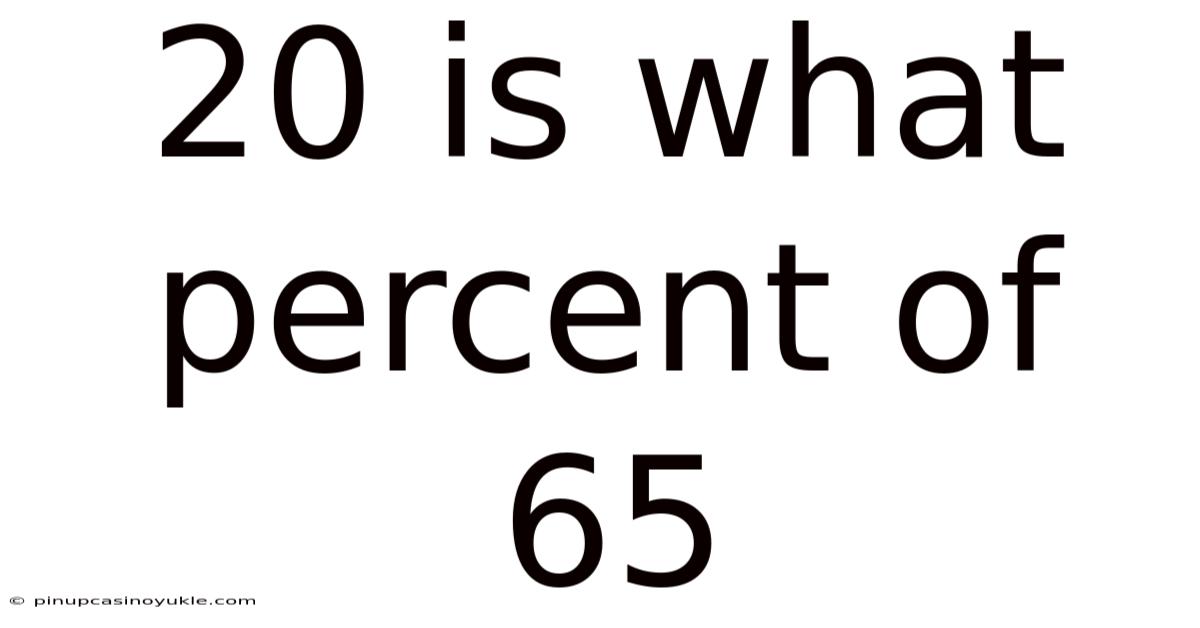
Table of Contents
Understanding percentages is a fundamental skill applicable in everyday life, from calculating discounts to understanding financial reports. When faced with a question like "20 is what percent of 65," it's essential to break down the problem into manageable steps. This article will guide you through the process of calculating percentages, offer real-world examples, and provide a deeper understanding of the underlying concepts.
Understanding the Basics of Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin "per centum," meaning "out of one hundred." Therefore, when we say "X percent," we mean X out of 100.
Key Concepts:
- Percentage: A ratio or fraction expressed as a part of 100.
- Base: The total or whole amount that the percentage is calculated from.
- Part: The portion of the base that we are interested in.
The Formula for Calculating Percentages
The basic formula to find what percentage one number is of another is:
(Part / Base) * 100 = Percentage
- Part: The value that is a fraction of the whole.
- Base: The total or whole value.
- Percentage: The result we want to find.
Step-by-Step Calculation: 20 is What Percent of 65?
Let's apply this formula to the question at hand: "20 is what percent of 65?"
1. Identify the Part and the Base:
- Part: 20
- Base: 65
2. Apply the Formula:
(20 / 65) * 100 = Percentage
3. Perform the Division:
20 / 65 ≈ 0.30769
4. Multiply by 100:
0. 30769 * 100 = 30.769
5. Round to an Appropriate Number of Decimal Places:
- Rounding to two decimal places gives us 30.77%.
Therefore, 20 is approximately 30.77% of 65.
Alternative Methods to Calculate Percentages
While the formula (Part / Base) * 100 is the most straightforward method, there are alternative approaches you can use to calculate percentages.
Method 1: Using Fractions
-
Express the Relationship as a Fraction:
- Write the relationship between the two numbers as a fraction. In this case, it's 20/65.
-
Simplify the Fraction (If Possible):
-
Simplify the fraction to its lowest terms. Both 20 and 65 are divisible by 5, so we can simplify the fraction:
20/65 = (20 ÷ 5) / (65 ÷ 5) = 4/13
-
-
Convert the Fraction to a Decimal:
-
Divide the numerator by the denominator to convert the fraction to a decimal:
4 ÷ 13 ≈ 0.30769
-
-
Convert the Decimal to a Percentage:
-
Multiply the decimal by 100 to express it as a percentage:
0. 30769 * 100 = 30.769%
-
-
Round if Necessary:
-
Round the percentage to the desired number of decimal places:
30. 769% ≈ 30.77%
-
Method 2: Using Proportions
-
Set up a Proportion:
-
A proportion is an equation stating that two ratios are equal. We can set up a proportion to solve for the percentage:
20/65 = x/100- Here, x represents the percentage we want to find.
-
-
Cross-Multiply:
-
Cross-multiply to solve for x:
20 * 100 = 65 * x 2000 = 65x
-
-
Solve for x:
-
Divide both sides by 65:
x = 2000 / 65 x ≈ 30.769
-
-
Round if Necessary:
-
Round the percentage to the desired number of decimal places:
x ≈ 30.77%
-
Method 3: Mental Math and Estimation
While not always precise, mental math and estimation can provide a quick approximation.
-
Estimate a Benchmark Percentage:
- Think of what percentage is close to the numbers you're working with. For example, 20 is about one-third of 60, and 60 is close to 65. So, we can estimate that 20 is a little more than one-third of 65.
-
Convert the Benchmark to a Percentage:
- One-third is approximately 33.33%. So, we know the answer will be slightly less than 33.33%.
-
Refine the Estimation:
- To refine the estimation, you can consider that 5 is about 7.7% of 65 (since 5/65 ≈ 0.0769). Therefore, 20 being compared to 65 will be slightly less than 33.33%.
-
Approximate the Answer:
- Based on this, we can estimate that 20 is around 30-33% of 65.
Practical Examples and Applications
Understanding how to calculate percentages is useful in various real-life scenarios.
Example 1: Calculating Discounts
Suppose a store offers a 20% discount on an item that originally costs $65. To find the discount amount:
-
Convert the Percentage to a Decimal:
- 20% = 0.20
-
Multiply by the Original Price:
- 0.20 * $65 = $13
The discount amount is $13. To find the final price:
- $65 - $13 = $52
The final price after the discount is $52.
Example 2: Calculating Sales Tax
If you buy an item for $20 and the sales tax is 6.5%, calculate the sales tax amount:
-
Convert the Percentage to a Decimal:
-
- 5% = 0.065
-
-
Multiply by the Item Price:
-
- 065 * $20 = $1.30
-
The sales tax amount is $1.30. The total cost is:
- $20 + $1.30 = $21.30
Example 3: Calculating Grades
Suppose you scored 20 points out of a possible 65 on a quiz. To find your grade as a percentage:
(20 / 65) * 100 ≈ 30.77%
Your grade on the quiz is approximately 30.77%.
Example 4: Analyzing Financial Data
Imagine a company's expenses are $65,000, and its marketing budget is $20,000. To find what percentage of the total expenses is allocated to marketing:
(20000 / 65000) * 100 ≈ 30.77%
Approximately 30.77% of the company's expenses are allocated to marketing.
Example 5: Calculating Tips
When you want to leave a 20% tip on a restaurant bill of $65:
-
Convert the Percentage to a Decimal:
- 20% = 0.20
-
Multiply by the Bill Amount:
- 0.20 * $65 = $13
You should leave a $13 tip.
Common Mistakes and How to Avoid Them
Calculating percentages can sometimes be tricky, and it's easy to make mistakes. Here are some common errors and how to avoid them:
-
Incorrectly Identifying the Base and the Part:
- Mistake: Confusing the base and the part can lead to incorrect calculations.
- Solution: Always clearly identify which number is the total (base) and which is the portion (part). For example, in "20 is what percent of 65," 65 is the base, and 20 is the part.
-
Forgetting to Multiply by 100:
- Mistake: Dividing the part by the base gives you a decimal, but you need to multiply by 100 to express it as a percentage.
- Solution: Always remember to multiply the result of the division by 100 to convert it to a percentage.
-
Rounding Errors:
- Mistake: Rounding too early or to an inappropriate number of decimal places can affect the accuracy of your result.
- Solution: Keep as many decimal places as possible during the calculation and only round at the final step. Use an appropriate number of decimal places based on the context (e.g., two decimal places for currency).
-
Misinterpreting the Question:
- Mistake: Not fully understanding what the question is asking can lead to using the wrong numbers in the calculation.
- Solution: Read the question carefully and make sure you understand what you are trying to find.
-
Using the Wrong Formula:
- Mistake: Applying the wrong formula or method can result in an incorrect answer.
- Solution: Ensure you are using the correct formula (Part / Base) * 100 for finding percentages.
-
Calculator Errors:
- Mistake: Incorrectly entering numbers into a calculator or making arithmetic errors.
- Solution: Double-check your entries and calculations to ensure accuracy.
Advanced Concepts in Percentages
Once you have a good grasp of basic percentage calculations, you can explore more advanced concepts.
Percentage Change
Percentage change is used to describe the degree to which a quantity changes over time. It is frequently used in finance to indicate the price change of a security.
The formula for percentage change is:
[(New Value - Old Value) / Old Value] * 100
-
Example: If a stock's price changes from $50 to $60, the percentage change is:
[($60 - $50) / $50] * 100 = (10 / 50) * 100 = 20%The stock's price increased by 20%.
Percentage Increase
Percentage increase is a specific type of percentage change where the new value is greater than the old value.
The formula for percentage increase is the same as for percentage change:
[(New Value - Old Value) / Old Value] * 100
-
Example: If a company's revenue increases from $100,000 to $120,000, the percentage increase is:
[($120,000 - $100,000) / $100,000] * 100 = (20,000 / 100,000) * 100 = 20%The company's revenue increased by 20%.
Percentage Decrease
Percentage decrease is a specific type of percentage change where the new value is less than the old value.
The formula for percentage decrease is:
[(Old Value - New Value) / Old Value] * 100
-
Example: If a product's price decreases from $80 to $60, the percentage decrease is:
[($80 - $60) / $80] * 100 = (20 / 80) * 100 = 25%The product's price decreased by 25%.
Weighted Averages
A weighted average is an average in which some values contribute more than others. It is used when some data points are more significant or occur more frequently.
To calculate a weighted average:
- Multiply each value by its weight.
- Add up all the results.
- Divide by the sum of the weights.
-
Example: Suppose a student's grade is based on the following:
- Homework: 20% weight, grade = 90
- Quizzes: 30% weight, grade = 80
- Final Exam: 50% weight, grade = 85
The weighted average is:
(0. 20 * 90) + (0.30 * 80) + (0.50 * 85) = 18 + 24 + 42.5 = 84.5The student's weighted average grade is 84.5.
Tools and Resources for Calculating Percentages
Various tools and resources are available to help you calculate percentages quickly and accurately.
Online Percentage Calculators
Numerous online percentage calculators can perform various percentage calculations. These calculators are easy to use and often provide step-by-step solutions.
- Calculator.net: Offers a wide range of percentage calculators, including calculators for finding percentage increase, decrease, and difference.
- Math is Fun: Provides a simple percentage calculator and explanations of percentage concepts.
- Good Calculators: Features a variety of financial and mathematical calculators, including percentage calculators.
Spreadsheet Software
Spreadsheet software like Microsoft Excel and Google Sheets can be used to perform percentage calculations.
-
Example in Excel:
-
If A1 contains the part (20) and B1 contains the base (65), you can use the following formula in C1:
=(A1/B1)*100This formula will calculate the percentage and display it in cell C1.
-
Mobile Apps
Several mobile apps are available for calculating percentages on the go.
- Percentage Calculator (Android): A simple and intuitive app for calculating percentages.
- Calculator Pro (iOS): A versatile calculator app with percentage calculation capabilities.
Conclusion
Understanding how to calculate percentages is an essential skill with wide-ranging applications in everyday life. Whether you are calculating discounts, analyzing financial data, or determining grades, the ability to work with percentages accurately is invaluable. By mastering the basic formula (Part / Base) * 100 and understanding the concepts discussed in this article, you can confidently tackle any percentage-related problem. Remember to identify the part and the base correctly, avoid common mistakes, and utilize available tools and resources to ensure accuracy.
Latest Posts
Latest Posts
-
How To Find Average Velocity Calculus
Nov 18, 2025
-
What Is The Role Of Rubisco In The Calvin Cycle
Nov 18, 2025
-
3 Lbs Equals How Many Ounces
Nov 18, 2025
-
How Many Ounces Are In A 1 2 Pound
Nov 18, 2025
-
Which Table Represents A Linear Function Edgenuity
Nov 18, 2025
Related Post
Thank you for visiting our website which covers about 20 Is What Percent Of 65 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.