2 Is What Percent Of 5
pinupcasinoyukle
Nov 20, 2025 · 7 min read
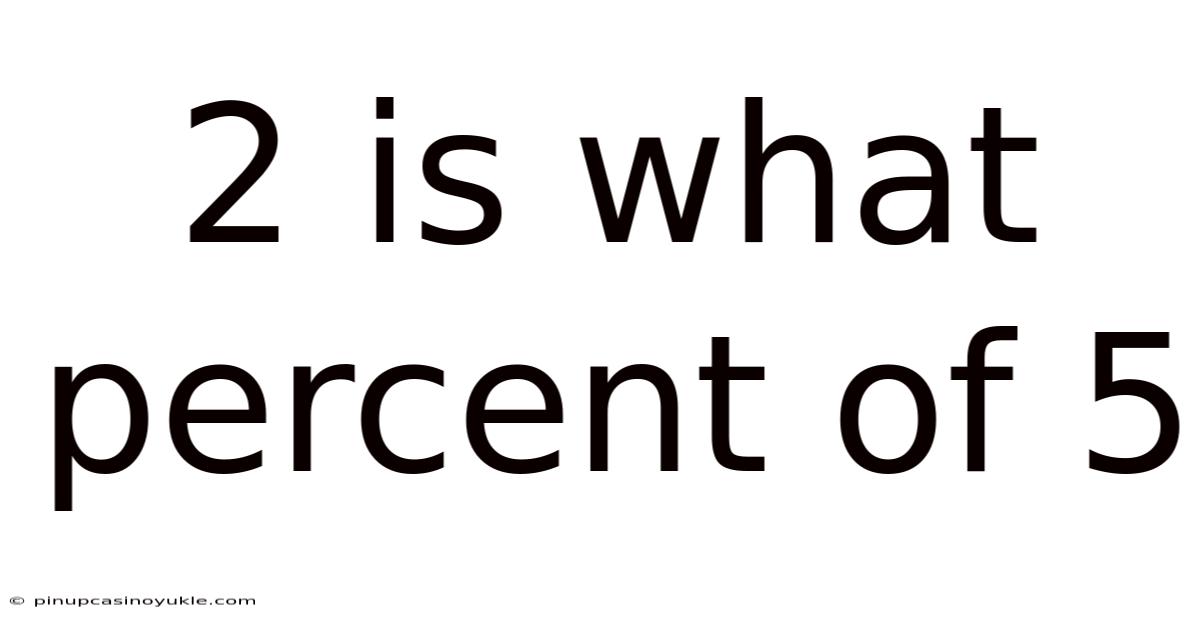
Table of Contents
Determining percentages is a fundamental skill applicable in various aspects of life, from calculating discounts while shopping to understanding financial reports. One common question that arises is, "2 is what percent of 5?" This simple question serves as an excellent starting point to delve into the world of percentages, ratios, and proportions.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "per hundred." Therefore, when we say 50 percent, we mean 50 out of 100. Percentages are used to express how large one quantity is relative to another quantity.
Basic Formula
The basic formula to calculate what percentage a number A is of a number B is:
Percentage = (A / B) * 100
In our case, A = 2 and B = 5.
Calculating "2 is What Percent of 5?"
To find out what percent 2 is of 5, we will use the formula mentioned above.
Step-by-Step Calculation
-
Identify the Values:
- A = 2 (the number we want to express as a percentage)
- B = 5 (the total or base number)
-
Apply the Formula:
- Percentage = (A / B) * 100
- Percentage = (2 / 5) * 100
-
Perform the Division:
- 2 / 5 = 0.4
-
Multiply by 100:
- 0.4 * 100 = 40
Therefore, 2 is 40% of 5.
Detailed Explanation
The calculation involves expressing 2 as a fraction of 5, which gives us 0.4. Multiplying this fraction by 100 converts it into a percentage. This means that 2 represents 40 parts out of 100 when compared to 5.
Why is This Important?
Understanding how to calculate percentages is crucial for:
- Financial Literacy: Calculating interest rates, discounts, and taxes.
- Data Analysis: Interpreting statistical data and reports.
- Everyday Life: Determining tips, understanding sales, and managing budgets.
Real-World Applications
Let's explore some real-world scenarios where this type of calculation is useful.
Scenario 1: Exam Scores
Suppose a student scores 2 out of 5 questions correctly on a quiz. To find the student's percentage score:
- Score = (2 / 5) * 100 = 40%
The student scored 40% on the quiz.
Scenario 2: Discount Calculation
If an item originally priced at $5 is on sale for $2 off, you can calculate the discount percentage:
- Discount Percentage = (2 / 5) * 100 = 40%
The item is on sale for a 40% discount.
Scenario 3: Resource Allocation
A project manager allocates 2 hours out of a 5-hour workday to a specific task. The percentage of time allocated to the task is:
- Time Allocation = (2 / 5) * 100 = 40%
40% of the workday is allocated to the specific task.
Understanding Ratios and Proportions
Percentages are closely related to ratios and proportions. A ratio is a comparison of two quantities, while a proportion is an equality between two ratios.
Ratios
In the question "2 is what percent of 5?", the ratio is 2:5. This ratio indicates the relative sizes of the two numbers.
Proportions
We can express the percentage calculation as a proportion:
2 / 5 = x / 100
Here, x represents the percentage we are trying to find. Solving for x gives us:
- x = (2 / 5) * 100
- x = 40
This confirms that 2 is 40% of 5.
Common Mistakes to Avoid
When calculating percentages, it's easy to make mistakes. Here are some common pitfalls to avoid:
- Incorrectly Identifying A and B: Ensure you correctly identify which number is the part (A) and which is the whole (B).
- Forgetting to Multiply by 100: The final step of multiplying by 100 is crucial to convert the decimal into a percentage.
- Misinterpreting the Question: Understand exactly what the question is asking. For example, "What is 2 percent of 5?" is different from "2 is what percent of 5?"
Alternative Methods to Calculate Percentages
While the formula (A / B) * 100 is the most straightforward method, there are alternative approaches to calculating percentages.
Method 1: Using Decimals
-
Divide A by B:
- 2 / 5 = 0.4
-
Convert the Decimal to a Percentage:
- Move the decimal point two places to the right: 0.4 becomes 40%.
Method 2: Using Fractions
-
Express A as a Fraction of B:
- 2 / 5
-
Convert the Fraction to an Equivalent Fraction with a Denominator of 100:
- (2 / 5) * (20 / 20) = 40 / 100
-
The Numerator is the Percentage:
- 40 / 100 = 40%
Advanced Applications of Percentages
Beyond basic calculations, percentages are used in more complex scenarios, such as calculating percentage change, compound interest, and statistical analysis.
Percentage Change
Percentage change is used to describe the relative difference between two values. The formula for percentage change is:
Percentage Change = [(New Value - Old Value) / Old Value] * 100
Example: If a price increases from $5 to $7, the percentage change is:
- Percentage Change = [(7 - 5) / 5] * 100 = (2 / 5) * 100 = 40%
The price increased by 40%.
Compound Interest
Compound interest is the interest calculated on the initial principal and also on the accumulated interest of previous periods. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (as a decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Example: If you invest $1000 at an annual interest rate of 5% compounded annually for 10 years:
- A = 1000 (1 + 0.05/1)^(1*10) = $1628.89
The future value of the investment after 10 years is $1628.89.
Statistical Analysis
Percentages are widely used in statistical analysis to express data in a standardized format, making it easier to compare different datasets.
Example: In a survey of 200 people, 80 people preferred Product A. The percentage of people who preferred Product A is:
- Percentage = (80 / 200) * 100 = 40%
40% of the people surveyed preferred Product A.
Tips for Mastering Percentage Calculations
- Practice Regularly: The more you practice, the more comfortable you will become with percentage calculations.
- Use Real-World Examples: Apply percentage calculations to everyday situations to reinforce your understanding.
- Understand the Underlying Concepts: Don't just memorize formulas; understand the logic behind them.
- Double-Check Your Work: Always double-check your calculations to avoid errors.
Conclusion
Understanding how to calculate percentages, such as determining that "2 is 40% of 5," is a valuable skill that has wide-ranging applications in various fields. By mastering the basic formula and understanding the underlying concepts, you can confidently tackle more complex percentage-related problems. Whether you're calculating discounts, analyzing data, or managing finances, a solid grasp of percentages will empower you to make informed decisions. Remember to practice regularly and apply your knowledge to real-world scenarios to solidify your understanding. With consistent effort, you'll become proficient in percentage calculations and be well-equipped to handle any percentage-related challenge that comes your way.
FAQ: Understanding Percentages
What is a percentage?
A percentage is a way of expressing a number as a fraction of 100. The term "percent" means "per hundred."
How do you calculate what percentage a number A is of a number B?
Use the formula: Percentage = (A / B) * 100
Why is it important to understand percentages?
Understanding percentages is crucial for financial literacy, data analysis, and making informed decisions in everyday life.
What are some common mistakes to avoid when calculating percentages?
Common mistakes include incorrectly identifying A and B, forgetting to multiply by 100, and misinterpreting the question.
Can you provide a real-world example of using percentages?
Sure, if an item originally priced at $5 is on sale for $2 off, you can calculate the discount percentage: Discount Percentage = (2 / 5) * 100 = 40%.
What is the relationship between percentages, ratios, and proportions?
Percentages are closely related to ratios and proportions. A ratio is a comparison of two quantities, while a proportion is an equality between two ratios.
How can I improve my percentage calculation skills?
Practice regularly, use real-world examples, understand the underlying concepts, and double-check your work.
What is percentage change and how is it calculated?
Percentage change is used to describe the relative difference between two values. The formula for percentage change is: Percentage Change = [(New Value - Old Value) / Old Value] * 100
What is compound interest and how does it relate to percentages?
Compound interest is the interest calculated on the initial principal and also on the accumulated interest of previous periods. It involves calculating percentages repeatedly over time.
How are percentages used in statistical analysis?
Percentages are widely used in statistical analysis to express data in a standardized format, making it easier to compare different datasets.
Latest Posts
Latest Posts
-
How Do You Be A Cop
Nov 20, 2025
-
How Many Electrons Does Copper Have
Nov 20, 2025
-
Political Ideology Concept Of Voting Behavior Interview Questions
Nov 20, 2025
-
Choose The Correct Description Of The Shape Of The Distribution
Nov 20, 2025
-
Which Type Of Function Is Shown In The Table Below
Nov 20, 2025
Related Post
Thank you for visiting our website which covers about 2 Is What Percent Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.