15 Of 35 Is What Percent
pinupcasinoyukle
Nov 21, 2025 · 7 min read
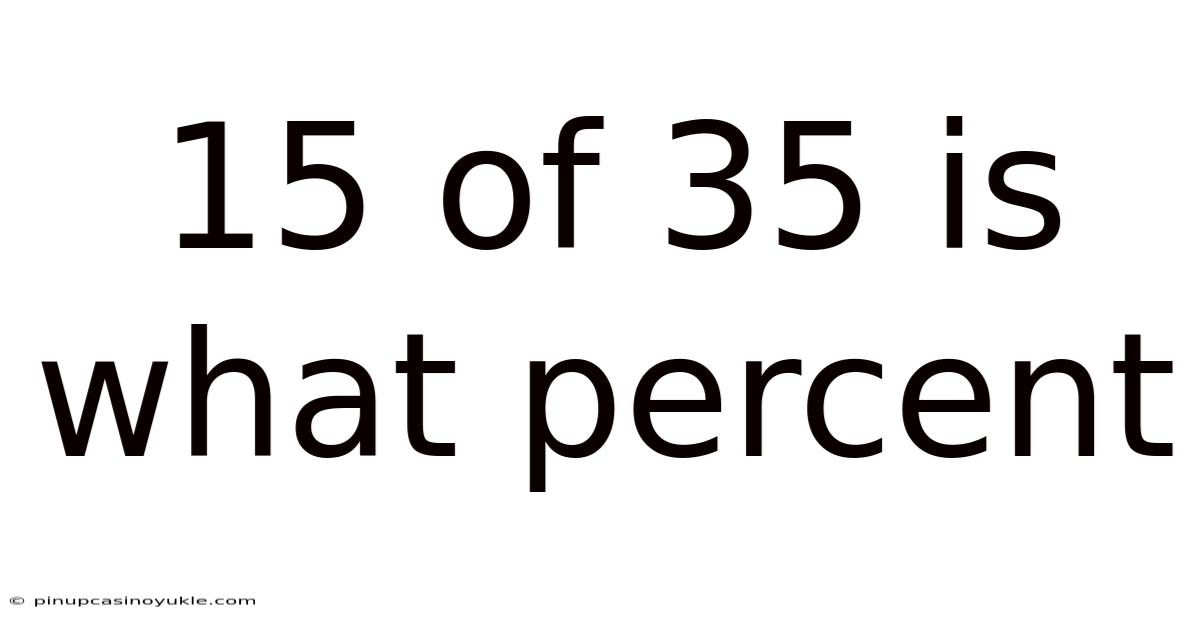
Table of Contents
Calculating percentages is a fundamental skill applicable across diverse fields, from everyday shopping to complex financial analyses. Understanding how to determine what percentage one number represents of another is not only academically useful but also practically essential. In this article, we will explore the concept of calculating percentages, specifically addressing the question: "15 of 35 is what percent?" This guide will provide a detailed explanation of the process, real-world examples, and additional insights to ensure you master this important skill.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin "per centum," meaning "out of one hundred." Percentages are used to express how large one quantity is relative to another quantity. They are a standardized way to compare different proportions, making it easier to understand relative values.
Basic Formula for Calculating Percentages
The basic formula to calculate what percentage a number (part) is of another number (whole) is:
Percentage = (Part / Whole) * 100
- Part: The number you want to express as a percentage of the whole.
- Whole: The total or reference number.
Applying the Formula to "15 of 35 is What Percent?"
In this specific question, we are asked to find out what percentage 15 is of 35. Here, 15 is the "part" and 35 is the "whole."
Using the formula:
Percentage = (15 / 35) * 100
Now, let's break down the calculation step by step.
Step-by-Step Calculation
To find what percentage 15 is of 35, follow these steps:
Step 1: Divide the Part by the Whole
First, divide the "part" (15) by the "whole" (35):
15 / 35 ≈ 0.42857
This division gives us a decimal number, which represents the fraction of 35 that 15 represents.
Step 2: Multiply by 100
Next, multiply the decimal number by 100 to convert it into a percentage:
0. 42857 * 100 ≈ 42.857
Step 3: Round to the Desired Precision
Depending on the context, you might want to round the percentage to a certain number of decimal places. For example, rounding to two decimal places, we get:
42.857 ≈ 42.86%
Therefore, 15 is approximately 42.86% of 35.
Real-World Examples
To illustrate the practical application of calculating percentages, let’s consider a few real-world examples.
Example 1: Calculating a Test Score
Suppose a student scores 15 marks out of a total of 35 in a test. To find the student's percentage score:
Percentage = (15 / 35) * 100 ≈ 42.86%
The student scored approximately 42.86% on the test.
Example 2: Determining a Discount
Imagine a store offers a discount of $15 on an item originally priced at $35. To calculate the percentage discount:
Percentage = (15 / 35) * 100 ≈ 42.86%
The discount is approximately 42.86% of the original price.
Example 3: Analyzing Sales Data
A company sells 15 units of a product out of a total potential market of 35 units. To find the market penetration rate:
Percentage = (15 / 35) * 100 ≈ 42.86%
The company has penetrated approximately 42.86% of the market.
Additional Insights and Tips
To further enhance your understanding and skills in calculating percentages, consider the following insights and tips.
Understanding the Context
Always consider the context of the problem. Understanding what the numbers represent can help you interpret the percentage correctly.
Using Proportions
Another way to solve percentage problems is by using proportions. For example, to find what percentage 15 is of 35, you can set up the proportion:
15 / 35 = x / 100
Solving for x:
x = (15 * 100) / 35 ≈ 42.86
Common Mistakes to Avoid
- Dividing in the wrong order: Ensure you divide the "part" by the "whole," not the other way around.
- Forgetting to multiply by 100: Remember to multiply the result by 100 to convert the decimal to a percentage.
- Misinterpreting the context: Understand the problem correctly to apply the formula appropriately.
Tools and Resources
Various tools and resources can help you calculate percentages accurately:
- Calculators: Use a basic calculator to perform the division and multiplication.
- Spreadsheet Software: Programs like Microsoft Excel or Google Sheets can be used to calculate percentages easily using formulas.
- Online Percentage Calculators: Numerous websites offer free percentage calculators that can provide quick and accurate results.
Advanced Percentage Calculations
Beyond the basic calculation, there are more complex percentage-related problems that you might encounter. Let's explore some of these advanced calculations.
Percentage Increase and Decrease
To calculate the percentage increase or decrease between two values, use the following formulas:
- Percentage Increase:
((New Value - Old Value) / Old Value) * 100 - Percentage Decrease:
((Old Value - New Value) / Old Value) * 100
Example: If a price increases from $35 to $50, the percentage increase is:
((50 - 35) / 35) * 100 ≈ 42.86%
If a price decreases from $35 to $20, the percentage decrease is:
((35 - 20) / 35) * 100 ≈ 42.86%
Calculating the Original Value
Sometimes, you might need to find the original value when you know the percentage and the resulting value. For example, if 15 is 20% of a number, you can find the original number as follows:
Let the original number be x.
0. 20 * x = 15
x = 15 / 0.20 = 75
So, 15 is 20% of 75.
Compound Percentage Changes
When dealing with successive percentage changes, you need to apply each percentage change sequentially. For example, if a price increases by 10% and then decreases by 5%, the final price is not simply a 5% increase.
Example: Suppose an item costs $100.
- Increase by 10%: $100 + (10% of $100) = $110
- Decrease by 5%: $110 - (5% of $110) = $104.50
The final price is $104.50, which is a 4.5% increase from the original price.
Common Applications of Percentages
Percentages are widely used in various fields and daily life situations. Here are some common applications:
Finance
- Interest Rates: Expressing the cost of borrowing money or the return on an investment.
- Investment Returns: Calculating the percentage gain or loss on investments.
- Budgeting: Allocating percentages of income to different expense categories.
Retail
- Discounts: Calculating price reductions during sales.
- Sales Tax: Adding a percentage of the purchase price as tax.
- Profit Margins: Determining the percentage of revenue that remains after deducting costs.
Education
- Grading: Calculating student scores and performance.
- Standardized Tests: Reporting scores as percentiles.
- Attendance Rates: Measuring the percentage of students present in class.
Health and Medicine
- Body Mass Index (BMI): Assessing weight status based on height and weight.
- Medication Dosages: Calculating the correct amount of medication based on body weight or other factors.
- Survival Rates: Reporting the percentage of patients who survive a particular disease or treatment.
Statistics and Data Analysis
- Survey Results: Presenting data as percentages to show the proportion of respondents who hold a particular view.
- Market Share: Measuring the percentage of a market controlled by a particular company or product.
- Error Rates: Calculating the percentage of errors in a process or system.
Tips for Mastering Percentage Calculations
To become proficient in calculating percentages, practice is essential. Here are some tips to help you master this skill:
Practice Regularly
The more you practice, the more comfortable you will become with the formulas and concepts. Try solving a variety of percentage problems to reinforce your understanding.
Use Real-Life Examples
Relate percentage calculations to real-life situations to make them more meaningful. For example, calculate discounts while shopping or track your expenses as a percentage of your income.
Understand the Underlying Concepts
Focus on understanding the underlying concepts rather than just memorizing formulas. This will help you apply the formulas correctly and solve more complex problems.
Check Your Work
Always check your work to ensure that your calculations are accurate. Use estimation to get a rough idea of the answer and then compare it to your calculated result.
Seek Help When Needed
Don't hesitate to seek help from teachers, tutors, or online resources if you are struggling with percentage calculations. There are many resources available to support your learning.
Conclusion
Calculating percentages is a fundamental skill that is essential for various aspects of life. The question "15 of 35 is what percent?" is a simple example that illustrates the basic principles of percentage calculation. By understanding the formula, practicing with real-world examples, and avoiding common mistakes, you can master this important skill. Whether you are calculating discounts, analyzing data, or managing your finances, a solid understanding of percentages will empower you to make informed decisions and solve problems effectively.
Latest Posts
Latest Posts
-
How To Tell If Triangles Are Similar
Nov 22, 2025
-
Identify The Structures Of The Eye In The Figure
Nov 22, 2025
-
Determine If The Relation Is A Function
Nov 22, 2025
-
What Is The Difference Between Equations And Expressions
Nov 22, 2025
-
The Expulsion From The Garden Of Eden Masaccio
Nov 22, 2025
Related Post
Thank you for visiting our website which covers about 15 Of 35 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.