15 Is What Percent Of 50
pinupcasinoyukle
Nov 17, 2025 · 7 min read
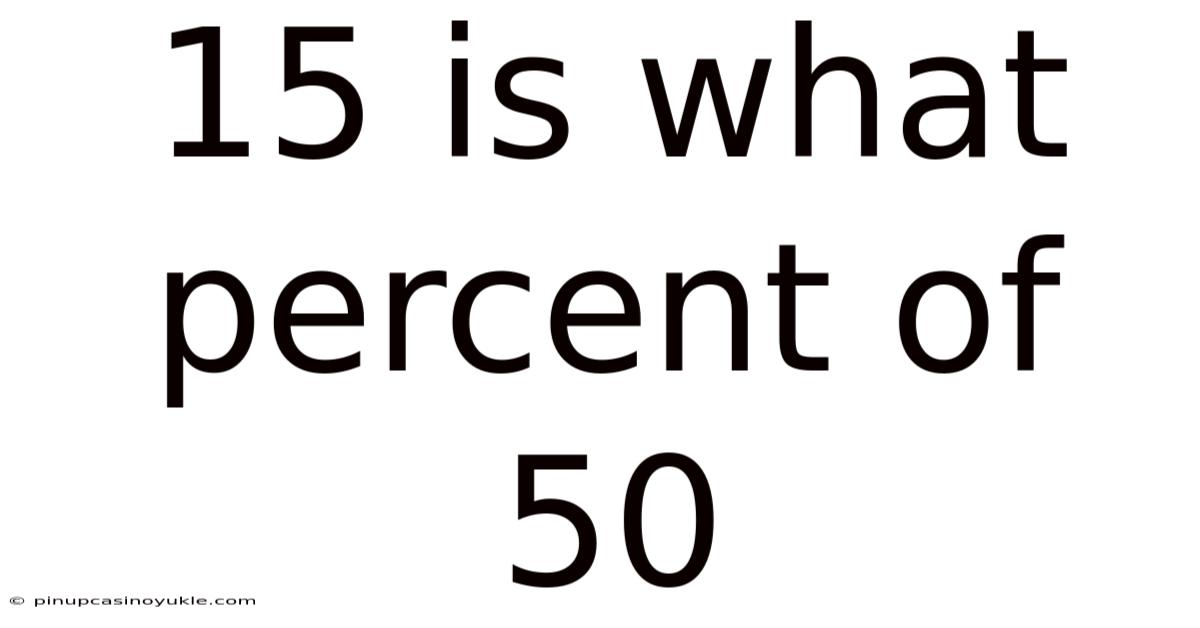
Table of Contents
Finding percentages is a fundamental skill applicable in various real-life scenarios, from calculating discounts to understanding statistical data. Determining what percentage one number represents of another is a common calculation. In this case, let's break down the process of figuring out "15 is what percent of 50."
Understanding Percentages
Before diving into the calculation, it's crucial to grasp the basics of percentages. A percentage is essentially a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." Therefore, when we say "X percent," we mean X out of every 100.
The Basic Formula
To calculate what percentage one number (the part) is of another number (the whole), you can use the following formula:
Percentage = (Part / Whole) * 100
In our specific question, "15 is what percent of 50," we identify:
- Part: 15
- Whole: 50
Step-by-Step Calculation
Let's apply the formula to our problem:
- Divide the part by the whole:
15 / 50 = 0.3 - Multiply the result by 100:
0.3 * 100 = 30
Therefore, 15 is 30% of 50.
Alternative Methods
While the formula is straightforward, understanding different approaches can provide a deeper insight and make calculations easier in certain situations.
Method 1: Using Fractions
- Express the relationship as a fraction:
- 15/50 represents the fraction of 50 that 15 constitutes.
- Simplify the fraction:
- Both 15 and 50 are divisible by 5.
- 15 ÷ 5 = 3
- 50 ÷ 5 = 10
- So, the simplified fraction is 3/10.
- Convert the fraction to a percentage:
- To convert a fraction to a percentage, multiply it by 100.
- (3/10) * 100 = 30%
Method 2: Setting Up a Proportion
A proportion states that two ratios are equal. In this case, we can set up a proportion to find the percentage.
- Set up the proportion:
- We want to find what percent (x) of 50 is 15. This can be written as:
x / 100 = 15 / 50
- We want to find what percent (x) of 50 is 15. This can be written as:
- Cross-multiply:
- Multiply x by 50 and 15 by 100.
50x = 1500
- Multiply x by 50 and 15 by 100.
- Solve for x:
- Divide both sides of the equation by 50.
x = 1500 / 50 x = 30
- Divide both sides of the equation by 50.
Therefore, 15 is 30% of 50.
Method 3: Mental Math Techniques
For simple percentages, mental math can be a quick and efficient way to find the answer.
- Find 10% of the whole:
- To find 10% of 50, divide 50 by 10.
- 50 / 10 = 5
- So, 10% of 50 is 5.
- Determine how many times 10% fits into the part:
- We need to find how many times 5 (10% of 50) fits into 15.
- 15 / 5 = 3
- Since 5 fits into 15 three times, 15 is three times 10% of 50.
- Multiply by 10 to find the percentage:
- 3 * 10% = 30%
Therefore, 15 is 30% of 50.
Practical Applications
Understanding how to calculate percentages has numerous practical applications in everyday life. Here are a few examples:
Discounts and Sales
When shopping, you often encounter discounts expressed as percentages. For example, if an item originally priced at $50 is on sale for 15% off, you can calculate the discount amount as follows:
- Calculate the discount amount:
- Discount = (Percentage Discount / 100) * Original Price
- Discount = (15 / 100) * $50
- Discount = 0.15 * $50
- Discount = $7.50
- Subtract the discount from the original price:
- Sale Price = Original Price - Discount
- Sale Price = $50 - $7.50
- Sale Price = $42.50
Therefore, the sale price of the item is $42.50.
Calculating Tips
When dining at a restaurant, it's customary to leave a tip for the server. A common tip amount is 15% to 20% of the total bill. If your bill is $50, you can calculate a 15% tip as follows:
- Calculate the tip amount:
- Tip = (Percentage / 100) * Bill Amount
- Tip = (15 / 100) * $50
- Tip = 0.15 * $50
- Tip = $7.50
Therefore, a 15% tip on a $50 bill is $7.50.
Understanding Grades
In academic settings, grades are often expressed as percentages. If you score 15 out of 50 on a quiz, your grade as a percentage is:
- Calculate the percentage:
- Percentage = (Score / Total Possible Score) * 100
- Percentage = (15 / 50) * 100
- Percentage = 0.3 * 100
- Percentage = 30%
Therefore, your grade on the quiz is 30%.
Financial Planning
Percentages are crucial in financial planning, such as calculating investment returns, interest rates, and budget allocations. For example, if you invest $50 in a stock and it earns $15 in dividends, the return on your investment as a percentage is:
- Calculate the percentage return:
- Percentage Return = (Earnings / Initial Investment) * 100
- Percentage Return = ($15 / $50) * 100
- Percentage Return = 0.3 * 100
- Percentage Return = 30%
Therefore, the return on your investment is 30%.
Data Analysis
In data analysis, percentages are used to represent proportions and distributions. For instance, if you survey 50 people and find that 15 of them prefer a particular product, the percentage of people who prefer the product is:
- Calculate the percentage:
- Percentage = (Number of People Who Prefer the Product / Total Number of People Surveyed) * 100
- Percentage = (15 / 50) * 100
- Percentage = 0.3 * 100
- Percentage = 30%
Therefore, 30% of the people surveyed prefer the product.
Common Mistakes to Avoid
While calculating percentages is relatively straightforward, it's essential to avoid common mistakes that can lead to incorrect answers:
- Incorrectly Identifying the Part and Whole:
- Ensure you correctly identify which number is the part and which is the whole. The "part" is the number you're trying to express as a percentage of the "whole."
- Forgetting to Multiply by 100:
- After dividing the part by the whole, remember to multiply the result by 100 to express it as a percentage.
- Rounding Errors:
- When dealing with decimals, be mindful of rounding errors. Round to an appropriate number of decimal places based on the context of the problem.
- Misunderstanding Percentage Increase or Decrease:
- When calculating percentage increase or decrease, make sure to use the correct formula:
- Percentage Increase = ((New Value - Old Value) / Old Value) * 100
- Percentage Decrease = ((Old Value - New Value) / Old Value) * 100
- When calculating percentage increase or decrease, make sure to use the correct formula:
Advanced Percentage Problems
Beyond the basic calculations, there are more complex percentage problems that require a deeper understanding of the concepts.
Finding the Whole When the Percentage and Part Are Known
Sometimes, you may need to find the whole when you know the percentage and the part. For example, if 15 is 30% of a number, you can find the number as follows:
- Set up the equation:
- Let x be the whole number.
- 30% of x = 15
- (30 / 100) * x = 15
-
- 3x = 15
- Solve for x:
- Divide both sides of the equation by 0.3.
- x = 15 / 0.3
- x = 50
Therefore, 15 is 30% of 50.
Calculating Compound Interest
Compound interest is the interest earned on both the initial principal and the accumulated interest from previous periods. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (as a decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
For example, if you invest $50 at an annual interest rate of 15% compounded annually for 10 years, the future value of your investment is:
A = 50 (1 + 0.15/1)^(1*10)
A = 50 (1.15)^10
A = 50 * 4.04555773570799
A = $202.28 (approximately)
Therefore, after 10 years, your investment will be worth approximately $202.28.
Percentages in Statistics
Percentages are frequently used in statistics to describe data sets and analyze trends. Common statistical measures involving percentages include:
- Percentage Change: Measures the relative change in a quantity over time.
- Percentiles: Indicate the relative standing of a particular value within a data set.
- Percentage Distribution: Shows the proportion of different categories within a data set.
Understanding these statistical applications of percentages is essential for interpreting and analyzing data effectively.
Conclusion
Calculating percentages is a vital skill with wide-ranging applications in everyday life, from shopping and dining to financial planning and data analysis. By understanding the basic formula and various calculation methods, you can confidently solve percentage problems and make informed decisions. Whether you're calculating discounts, tips, grades, or investment returns, mastering percentages will empower you to navigate the world with greater financial literacy and analytical prowess. Remember to practice and apply these concepts regularly to strengthen your understanding and enhance your problem-solving abilities.
Latest Posts
Latest Posts
-
How Many Oz In 50 Pounds
Nov 17, 2025
-
56 Oz Is How Many Pounds
Nov 17, 2025
-
Terms In Science That Start With F
Nov 17, 2025
-
If S Glyceraldehyde Has A Specific Rotation Of
Nov 17, 2025
-
What Is The Difference Between Asexual Reproduction And Sexual Reproduction
Nov 17, 2025
Related Post
Thank you for visiting our website which covers about 15 Is What Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.