12 Is What Percent Of 20
pinupcasinoyukle
Nov 05, 2025 · 7 min read
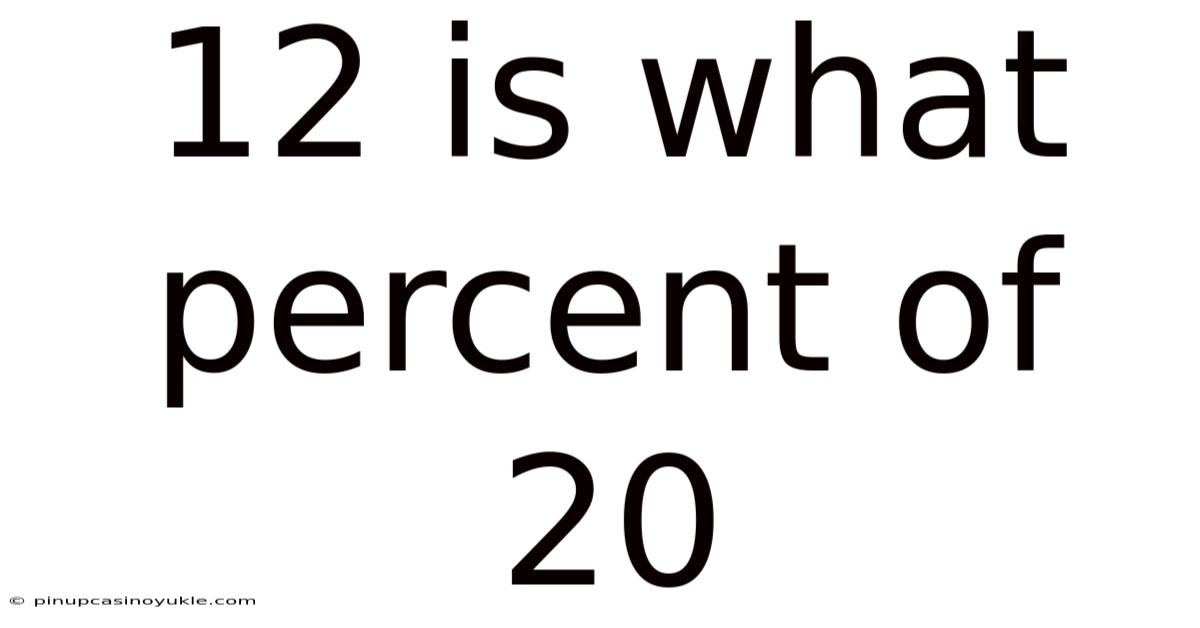
Table of Contents
Calculating percentages is a fundamental skill applicable in various real-life scenarios, from figuring out discounts at the store to understanding statistical data. The question "12 is what percent of 20" is a straightforward percentage problem that can be solved using basic arithmetic. Mastering this type of calculation provides a solid foundation for more complex mathematical concepts and everyday financial literacy.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." In essence, percentages are used to show relative proportions and are denoted by the symbol %.
Basic Formula
The fundamental formula to calculate percentages is:
(Part / Whole) * 100 = Percentage
Where:
- Part is the specific quantity you are interested in.
- Whole is the total or reference quantity.
- Percentage is the value you are trying to find, expressed as a percentage.
Step-by-Step Calculation: 12 is What Percent of 20?
To determine what percent 12 is of 20, we follow these steps:
Step 1: Identify the Part and the Whole
In this problem:
- Part = 12
- Whole = 20
Step 2: Apply the Formula
Using the formula (Part / Whole) * 100 = Percentage, we substitute the values:
(12 / 20) * 100 = Percentage
Step 3: Perform the Division
Divide 12 by 20:
12 / 20 = 0.6
Step 4: Multiply by 100
Multiply the result by 100 to convert it to a percentage:
0.6 * 100 = 60
Step 5: State the Result
Therefore, 12 is 60% of 20.
Alternative Methods to Calculate Percentages
While the basic formula is the most common method, there are alternative ways to calculate percentages that can be useful in different situations.
Method 1: Using Proportions
A proportion is an equation that states that two ratios are equal. In the context of percentages, we can set up a proportion to solve for the unknown percentage.
The proportion can be written as:
Part / Whole = Percentage / 100
In our case:
12 / 20 = x / 100
To solve for x (the percentage), we cross-multiply:
12 * 100 = 20 * x
1200 = 20x
Divide both sides by 20:
x = 1200 / 20
x = 60
So, 12 is 60% of 20.
Method 2: Simplifying Fractions
Sometimes, simplifying the fraction before converting it to a percentage can make the calculation easier.
Starting with the fraction 12 / 20, we can simplify it by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 4:
12 / 4 = 3
20 / 4 = 5
So, the simplified fraction is 3 / 5.
Now, convert this fraction to a percentage:
(3 / 5) * 100
3 / 5 = 0.6
0.6 * 100 = 60
Thus, 12 is 60% of 20.
Real-World Applications
Understanding how to calculate percentages is useful in many practical situations. Here are a few examples:
Calculating Discounts
When shopping, discounts are often expressed as percentages. For example, if an item originally priced at $20 is 12% off, you can calculate the discount amount:
Discount = (Percentage / 100) * Original Price
Discount = (12 / 100) * 20
Discount = 0.12 * 20
Discount = $2.40
The discounted price is then:
Original Price - Discount = $20 - $2.40 = $17.60
Determining Grades
In academic settings, grades are often calculated as percentages. If a student scores 12 out of 20 on a quiz, their grade as a percentage is:
(12 / 20) * 100 = 60%
Analyzing Sales Data
Businesses use percentages to analyze sales data. For instance, if a company's sales increased from $20,000 to $32,000, the percentage increase can be calculated:
Increase = New Value - Original Value = $32,000 - $20,000 = $12,000
Percentage Increase = (Increase / Original Value) * 100
Percentage Increase = ($12,000 / $20,000) * 100
Percentage Increase = 0.6 * 100 = 60%
Calculating Tips
When dining out, calculating a tip is a common application of percentages. If your bill is $20 and you want to leave a 12% tip:
Tip Amount = (Percentage / 100) * Bill Amount
Tip Amount = (12 / 100) * 20
Tip Amount = 0.12 * 20
Tip Amount = $2.40
Understanding Financial Growth
Percentages are crucial in understanding financial growth, such as investment returns. If an investment of $20 grows to $32, the percentage growth is:
Growth = New Value - Original Value = $32 - $20 = $12
Percentage Growth = (Growth / Original Value) * 100
Percentage Growth = ($12 / $20) * 100
Percentage Growth = 0.6 * 100 = 60%
Common Mistakes and How to Avoid Them
Calculating percentages is generally straightforward, but there are common mistakes to watch out for:
Misidentifying the Part and the Whole
One of the most frequent errors is confusing the part and the whole. Always ensure that you correctly identify which value represents the total (whole) and which represents the specific portion (part) you are interested in.
Example: If the question is "What percent of 50 is 25?", make sure you recognize that 50 is the whole and 25 is the part.
Incorrectly Applying the Formula
Applying the formula incorrectly can lead to wrong answers. Double-check that you are dividing the part by the whole and then multiplying by 100.
Example: Ensure you calculate (Part / Whole) * 100 and not (Whole / Part) * 100.
Arithmetic Errors
Simple arithmetic mistakes can throw off your calculations. Always double-check your division and multiplication.
Example: Ensure that 12 / 20 is calculated correctly as 0.6 and that 0.6 * 100 is 60.
Forgetting to Multiply by 100
Failing to multiply by 100 after dividing the part by the whole will give you a decimal or fraction instead of a percentage.
Example: If you calculate 12 / 20 = 0.6, remember to multiply by 100 to get 60%.
Rounding Errors
In some cases, you may need to round your answer. Be careful to round correctly and according to the instructions provided (if any).
Example: If the result is 60.333%, you may need to round it to 60.33% or 60.3%, depending on the required precision.
Advanced Percentage Problems
Once you've mastered the basics, you can tackle more complex percentage problems. Here are a few examples:
Percentage Increase and Decrease
Calculating the percentage increase or decrease involves comparing a new value to an original value. The formula is:
Percentage Change = ((New Value - Original Value) / Original Value) * 100
Example: If a price increases from $20 to $25, the percentage increase is:
((25 - 20) / 20) * 100 = (5 / 20) * 100 = 25%
Finding the Original Value
Sometimes, you need to find the original value when you know the percentage and the part.
Example: 12 is 20% of what number?
Let x be the original number. Then:
0.20 * x = 12
x = 12 / 0.20
x = 60
So, 12 is 20% of 60.
Compound Percentages
Compound percentages involve multiple percentage changes applied sequentially.
Example: If a price increases by 10% and then decreases by 5%, the overall percentage change is not simply 5%.
First, calculate the price after the 10% increase:
New Price = Original Price * (1 + Percentage Increase)
If the original price is $100:
New Price = 100 * (1 + 0.10) = $110
Next, calculate the price after the 5% decrease:
Final Price = New Price * (1 - Percentage Decrease)
Final Price = 110 * (1 - 0.05) = 110 * 0.95 = $104.50
The overall percentage change is:
((104.50 - 100) / 100) * 100 = 4.5%
Using Percentages in Statistics
Percentages are frequently used in statistics to represent proportions and distributions. For example, if you have a dataset of 200 people and 30 of them are in a certain category, the percentage is:
(30 / 200) * 100 = 15%
Tools for Calculating Percentages
While it's important to understand the underlying principles, various tools can help you calculate percentages quickly and accurately:
Calculators
Basic calculators have percentage functions that simplify the calculation process. You can directly input the values and get the percentage result.
Spreadsheet Software
Programs like Microsoft Excel or Google Sheets have built-in functions for calculating percentages. You can use formulas like =(A1/B1)*100 to calculate the percentage of the value in cell A1 compared to the value in cell B1.
Online Percentage Calculators
Numerous websites offer free percentage calculators. These tools are convenient for quick calculations and often provide additional functionalities, such as calculating percentage increases, decreases, and differences.
Mobile Apps
Many mobile apps are designed for performing percentage calculations. These apps are handy for on-the-go calculations and often include features like tip calculators and discount calculators.
Conclusion
Understanding how to calculate percentages is an essential skill with wide-ranging applications in everyday life. Whether you're figuring out discounts, analyzing data, or understanding financial growth, mastering percentage calculations empowers you to make informed decisions. By following the step-by-step methods, understanding common mistakes, and utilizing available tools, you can confidently tackle any percentage problem. The calculation "12 is what percent of 20?" serves as a fundamental example that, once understood, opens the door to more complex and practical applications.
Latest Posts
Latest Posts
-
What Does Y Mean In Math
Nov 05, 2025
-
Are Diagonals In A Rhombus Perpendicular
Nov 05, 2025
-
What Word Describes The Equal Shares Of The Shape Answer
Nov 05, 2025
-
Where Do The Light Reactions Of Photosynthesis Take Place
Nov 05, 2025
-
How To Solve An Absolute Value Inequality
Nov 05, 2025
Related Post
Thank you for visiting our website which covers about 12 Is What Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.