1 Is What Percent Of 10
pinupcasinoyukle
Nov 11, 2025 · 7 min read
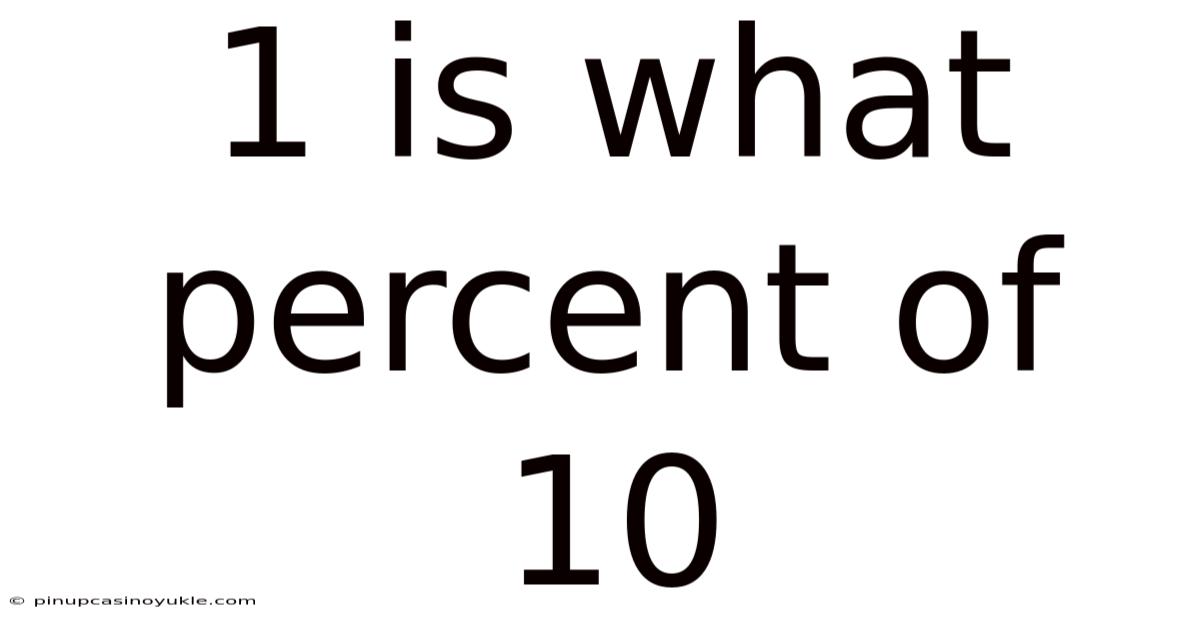
Table of Contents
The question "1 is what percent of 10" is a fundamental concept in mathematics, particularly related to percentages. Understanding how to calculate percentages is crucial in various aspects of daily life, from figuring out discounts while shopping to understanding statistics in the news. This article will thoroughly explore the calculation of this specific percentage, provide context, examples, and delve into the broader applications of percentage calculations.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "per hundred." When we say "1 is what percent of 10," we're essentially asking, "How many parts out of 100 is 1 if we consider 10 as the whole?"
To calculate a percentage, you generally use the formula:
Percentage = (Part / Whole) * 100
Where:
- Part is the value you want to express as a percentage of the whole.
- Whole is the total or reference value.
In our specific case, 1 is the part, and 10 is the whole.
Calculating "1 is What Percent of 10"
Using the formula, let's calculate what percentage 1 represents of 10.
-
Identify the Part and the Whole:
- Part = 1
- Whole = 10
-
Apply the Formula:
- Percentage = (1 / 10) * 100
-
Perform the Calculation:
- Percentage = 0.1 * 100
- Percentage = 10%
Therefore, 1 is 10% of 10.
Step-by-Step Breakdown
To ensure clarity, let's break down the calculation step-by-step:
-
Division:
- Divide the part (1) by the whole (10):
1 ÷ 10 = 0.1
- Divide the part (1) by the whole (10):
-
Multiplication:
- Multiply the result by 100 to convert it to a percentage:
0.1 * 100 = 10
- Multiply the result by 100 to convert it to a percentage:
The result, 10, represents the percentage. Hence, 1 is 10% of 10.
Why is This Calculation Important?
Understanding how to calculate percentages is not just an academic exercise; it has numerous practical applications in everyday life. Here are a few reasons why this calculation and similar percentage problems are important:
- Financial Literacy: Percentages are used to calculate interest rates, discounts, taxes, and investment returns.
- Retail and Shopping: Knowing how to calculate percentages helps in determining the actual price after a discount.
- Statistics and Data Analysis: Percentages are used to interpret data, understand survey results, and analyze trends.
- Science and Engineering: Percentages are used in experiments, measurements, and calculations.
- Everyday Decision Making: From calculating tips at restaurants to understanding the nutritional content of food, percentages play a crucial role in daily decisions.
Real-World Examples and Applications
To further illustrate the importance of understanding percentages, let's explore some real-world examples:
Example 1: Calculating Discounts
Suppose a store offers a 20% discount on an item that costs $50. To find the discount amount:
- Discount Percentage = 20%
- Original Price = $50
- Convert the percentage to a decimal:
20% = 20 / 100 = 0.20 - Multiply the original price by the decimal:
0.20 * $50 = $10
So, the discount is $10, and the final price is $50 - $10 = $40.
Example 2: Calculating Sales Tax
If the sales tax is 6% on a purchase of $100:
- Sales Tax Percentage = 6%
- Purchase Amount = $100
- Convert the percentage to a decimal:
6% = 6 / 100 = 0.06 - Multiply the purchase amount by the decimal:
0.06 * $100 = $6
The sales tax is $6, and the total amount to be paid is $100 + $6 = $106.
Example 3: Investment Returns
If you invest $2000 and earn a 5% return:
- Return Percentage = 5%
- Investment Amount = $2000
- Convert the percentage to a decimal:
5% = 5 / 100 = 0.05 - Multiply the investment amount by the decimal:
0.05 * $2000 = $100
The return on your investment is $100, and the total amount you have is $2000 + $100 = $2100.
Example 4: Test Scores
If you score 80 out of 100 on a test, your percentage score is:
- Score = 80
- Total Marks = 100
- Apply the formula:
Percentage = (80 / 100) * 100 - Calculate:
Percentage = 0.8 * 100 = 80%
You scored 80% on the test.
Variations of Percentage Problems
While the basic formula remains the same, percentage problems can present in various forms. Understanding these variations is essential for mastering percentage calculations.
Finding What Percent One Number is of Another
This is the type of problem we initially addressed: "1 is what percent of 10." The general form is:
X is what percent of Y?
Use the formula: Percentage = (X / Y) * 100
Finding a Percentage of a Number
This involves calculating a specific percentage of a given number. For example:
What is 25% of 80?
- Convert the percentage to a decimal:
25% = 25 / 100 = 0.25 - Multiply the number by the decimal:
0.25 * 80 = 20
So, 25% of 80 is 20.
Finding the Whole When a Percentage is Known
This involves finding the total amount when you know a percentage of it. For example:
15 is 30% of what number?
Let the number be Z. Then:
30% of Z = 15
- Convert the percentage to a decimal:
30% = 30 / 100 = 0.30 - Set up the equation:
0.30 * Z = 15 - Solve for Z:
Z = 15 / 0.30 = 50
So, 15 is 30% of 50.
Percentage Increase and Decrease
-
Percentage Increase: Represents how much a quantity has increased relative to its original value.
Formula:
Percentage Increase = ((New Value - Original Value) / Original Value) * 100 -
Percentage Decrease: Represents how much a quantity has decreased relative to its original value.
Formula:
Percentage Decrease = ((Original Value - New Value) / Original Value) * 100
For example, if a price increases from $20 to $25:
Percentage Increase = (($25 - $20) / $20) * 100 = (5 / 20) * 100 = 25%
If a price decreases from $25 to $20:
Percentage Decrease = (($25 - $20) / $25) * 100 = (5 / 25) * 100 = 20%
Common Mistakes to Avoid
While percentage calculations are relatively straightforward, there are common mistakes that people often make. Being aware of these mistakes can help you avoid them:
-
Incorrectly Identifying the Part and the Whole:
- Ensure you correctly identify which number is the part and which is the whole. The whole is the reference value, and the part is what you're expressing as a percentage of that whole.
-
Forgetting to Multiply by 100:
- After dividing the part by the whole, remember to multiply the result by 100 to express it as a percentage.
-
Misinterpreting Percentage Increase and Decrease:
- When calculating percentage increase or decrease, make sure you use the correct formula and identify the original and new values accurately.
-
Rounding Errors:
- When dealing with decimal percentages, be mindful of rounding errors. Rounding too early in the calculation can lead to inaccurate results.
-
Confusion with Decimals and Fractions:
- Ensure you are comfortable converting percentages to decimals and fractions and vice versa. This is crucial for accurate calculations.
Advanced Percentage Concepts
Beyond the basic calculations, there are more advanced concepts involving percentages that are useful in specific contexts.
Compound Interest
Compound interest is the interest calculated on the initial principal, which also includes all of the accumulated interest from previous periods. This is a powerful concept in finance and investment. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (as a decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Percentage Change in Statistics
In statistics, percentage change is used to describe the relative change in a quantity. It is often used to analyze data and trends.
Formula: Percentage Change = ((New Value - Old Value) / Old Value) * 100
Weighted Averages
A weighted average is an average in which some values contribute more than others. Percentages are often used to assign weights to different values.
For example, if a student's final grade is calculated as follows:
- Homework: 20%
- Quizzes: 30%
- Final Exam: 50%
And the student scores:
- Homework: 90%
- Quizzes: 80%
- Final Exam: 85%
Then the weighted average is:
(0.20 * 90) + (0.30 * 80) + (0.50 * 85) = 18 + 24 + 42.5 = 84.5%
Tools and Resources for Percentage Calculations
There are numerous tools and resources available to help with percentage calculations:
- Calculators: Basic calculators have percentage functions that can simplify calculations.
- Online Percentage Calculators: Numerous websites offer percentage calculators that can handle various types of percentage problems.
- Spreadsheet Software: Programs like Microsoft Excel and Google Sheets can perform complex percentage calculations and data analysis.
- Mobile Apps: Many mobile apps are designed for quick and easy percentage calculations on the go.
Conclusion
Understanding how to calculate percentages is a fundamental skill with wide-ranging applications in daily life. The question "1 is what percent of 10" serves as a basic example to illustrate the core concepts of percentage calculations. By mastering the basic formula and understanding the different types of percentage problems, you can confidently tackle various real-world scenarios involving percentages. Whether it's calculating discounts, understanding financial data, or analyzing statistics, a solid understanding of percentages is an invaluable asset.
Latest Posts
Latest Posts
-
How To Get Rid Of A Fraction
Nov 12, 2025
-
How Much Does Online Homeschooling Cost
Nov 12, 2025
-
How Much Energy Is Lost At Each Trophic Level
Nov 12, 2025
-
How To Use Distributive Property To Remove Parentheses
Nov 12, 2025
-
What Is B In The Slope Intercept Form
Nov 12, 2025
Related Post
Thank you for visiting our website which covers about 1 Is What Percent Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.