1 2 X 1 2 X 1 2
pinupcasinoyukle
Nov 02, 2025 · 9 min read
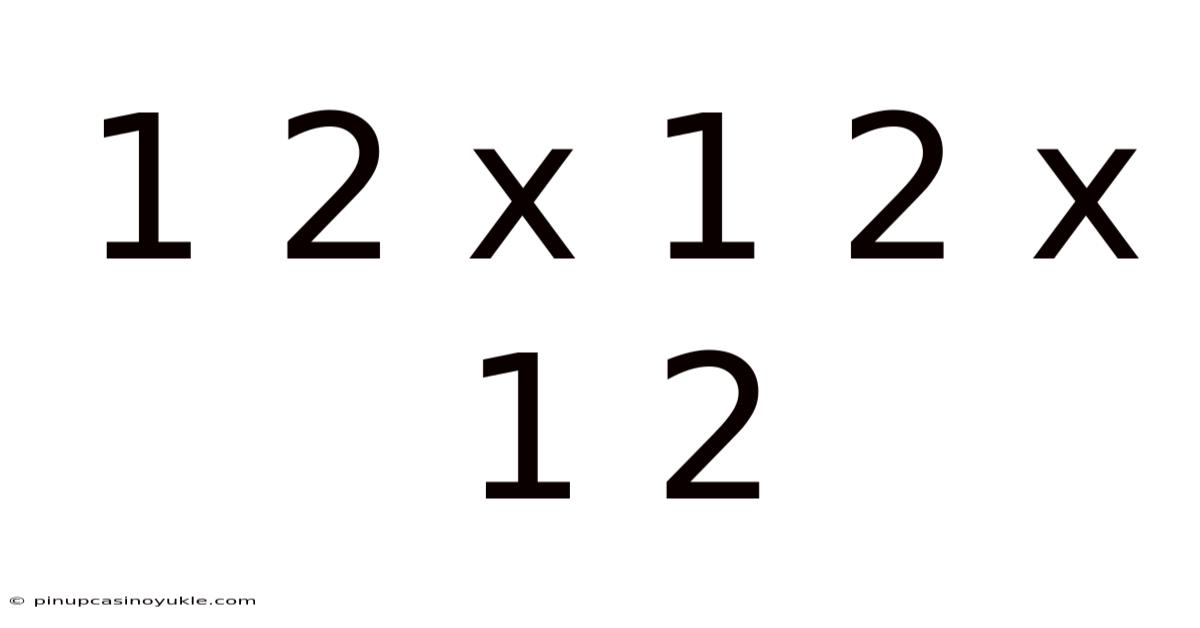
Table of Contents
Unraveling the Mystery of 1 2 x 1 2 x 1 2: A Deep Dive into Mathematics and Beyond
The seemingly simple expression "1 2 x 1 2 x 1 2" holds within it layers of mathematical understanding and diverse applications. While at its core, it represents a straightforward multiplication, exploring its meaning allows us to delve into concepts like fractions, decimals, exponents, volume calculations, and even probability. This article aims to dissect "1 2 x 1 2 x 1 2" from various angles, offering a comprehensive understanding suitable for readers with different mathematical backgrounds.
The Basics: Multiplication and Fractions
At its most fundamental level, "1 2 x 1 2 x 1 2" represents the multiplication of three identical fractions: one-half multiplied by one-half, multiplied again by one-half. Understanding what a fraction represents is crucial. A fraction, like 1/2, represents a part of a whole. The number below the line (the denominator, in this case, 2) indicates the total number of equal parts the whole is divided into. The number above the line (the numerator, in this case, 1) indicates how many of those parts we're considering.
Therefore, 1/2 represents one part out of two equal parts that make up a whole. Multiplying fractions involves multiplying the numerators together and the denominators together. Let's break it down step-by-step:
-
1/2 x 1/2: Multiply the numerators (1 x 1 = 1) and the denominators (2 x 2 = 4). The result is 1/4. This means one-half of one-half equals one-quarter.
-
(1/4) x 1/2: Now, multiply the result (1/4) by the remaining 1/2. Multiply the numerators (1 x 1 = 1) and the denominators (4 x 2 = 8). The final result is 1/8.
Therefore, 1 2 x 1 2 x 1 2 = 1/8. This means one-half of one-half of one-half equals one-eighth.
Converting to Decimals: An Alternative Representation
Fractions and decimals are two different ways of representing the same values. The fraction 1/2 can be easily converted to the decimal 0.5. To perform the same calculation using decimals, we substitute 1/2 with 0.5:
-
5 x 0.5 x 0.5
-
5 x 0.5: This equals 0.25 (twenty-five hundredths).
-
25 x 0.5: This equals 0.125 (one hundred twenty-five thousandths).
Therefore, 0.5 x 0.5 x 0.5 = 0.125. Notice that 0.125 is the decimal equivalent of the fraction 1/8. This demonstrates that whether we use fractions or decimals, the underlying mathematical relationship remains the same.
Exponents: A More Concise Notation
Exponents provide a shorthand way to represent repeated multiplication of the same number. Instead of writing 1 2 x 1 2 x 1 2, we can express it as (1/2)<sup>3</sup> or 0.5<sup>3</sup>. The base (1/2 or 0.5) is the number being multiplied, and the exponent (3) indicates how many times the base is multiplied by itself.
In this case, (1/2)<sup>3</sup> means 1/2 multiplied by itself three times, which, as we've already established, equals 1/8. Similarly, 0.5<sup>3</sup> means 0.5 multiplied by itself three times, resulting in 0.125.
Understanding exponents is crucial for more advanced mathematical concepts and simplifies complex calculations.
Visualizing 1 2 x 1 2 x 1 2: Volume and Geometry
The expression "1 2 x 1 2 x 1 2" can be visualized geometrically, particularly in the context of volume. Imagine a cube with sides of length 1 unit (e.g., 1 meter, 1 foot, 1 inch). The volume of this cube is 1 x 1 x 1 = 1 cubic unit.
Now, imagine cutting this cube in half along each of its three dimensions (length, width, and height). Each cut divides the dimension in half, resulting in a length, width, and height of 1/2 unit each. The smaller cube created by these cuts has a volume of 1 2 x 1 2 x 1 2 = 1/8 cubic units.
This visualization illustrates that the smaller cube occupies one-eighth of the volume of the original cube. This concept is fundamental in understanding scaling and proportions in geometry.
Practical Applications: Recipes and Proportions
The concept of multiplying fractions, especially by 1/2, is frequently encountered in everyday life, particularly in cooking and baking. Recipes often need to be scaled up or down depending on the number of servings required. Multiplying by 1/2 is equivalent to halving a quantity.
For example, if a recipe calls for 1 cup of flour and you only want to make half the recipe, you would multiply 1 cup by 1/2, resulting in 1/2 cup of flour. If the recipe further instructs to use half of the halved quantity, that's another multiplication by 1/2 (or 0.5 x 0.5 = 0.25 of the original).
Understanding how to manipulate fractions and decimals is essential for accurate ingredient measurements and consistent results in the kitchen.
Probability: Exploring the Odds
The expression "1 2 x 1 2 x 1 2" also finds application in probability. Consider a scenario where you flip a fair coin three times. A fair coin has two equally likely outcomes: heads (H) or tails (T). The probability of getting heads on a single flip is 1/2, and the probability of getting tails is also 1/2.
What is the probability of getting heads on all three flips (HHH)? Since each coin flip is independent (the outcome of one flip doesn't affect the outcome of the others), we multiply the probabilities of each individual event:
- Probability of getting heads on the first flip: 1/2
- Probability of getting heads on the second flip: 1/2
- Probability of getting heads on the third flip: 1/2
Therefore, the probability of getting three heads in a row is 1 2 x 1 2 x 1 2 = 1/8. This means that, on average, you would expect to get three heads in a row once every eight sets of three coin flips.
This example demonstrates how the multiplication of fractions is used to calculate the probability of independent events occurring in sequence.
Beyond the Basics: Exploring More Complex Scenarios
While we've focused on the straightforward multiplication of 1/2 by itself three times, the underlying principles can be extended to more complex scenarios involving different fractions and more variables. For example, consider the expression:
(1/3) x (1/4) x (1/2)
This expression represents taking one-third of one-quarter of one-half. The calculation is similar: multiply the numerators (1 x 1 x 1 = 1) and the denominators (3 x 4 x 2 = 24). The result is 1/24.
Similarly, we could explore expressions with different exponents, such as (1/2)<sup>5</sup>, which represents 1/2 multiplied by itself five times. The result would be 1/32.
The key takeaway is that understanding the fundamental principles of fraction multiplication allows you to tackle a wide range of mathematical problems.
The Importance of Understanding Fractions and Decimals
The ability to work confidently with fractions and decimals is a foundational skill in mathematics and has far-reaching implications in various fields. From basic arithmetic to advanced calculus, a solid understanding of these concepts is essential for success.
Furthermore, practical skills like budgeting, investing, and home improvement often require the use of fractions and decimals. Whether you're calculating discounts at the store, determining mortgage payments, or measuring materials for a construction project, a strong grasp of these concepts will empower you to make informed decisions.
Common Misconceptions and How to Avoid Them
Despite its seemingly simple nature, "1 2 x 1 2 x 1 2" and related concepts can sometimes lead to common misconceptions. Here are a few examples:
-
Thinking that multiplying by a fraction always makes the result larger: This is incorrect. Multiplying by a fraction less than 1 (like 1/2) actually decreases the value. This is because you are taking a part of the original number, not increasing it.
-
Confusing fractions and decimals: While fractions and decimals represent the same values, they are written differently. It's important to understand how to convert between them and to choose the representation that is most appropriate for the situation.
-
Incorrectly multiplying fractions: Remember to multiply the numerators together and the denominators together. A common mistake is to add the numerators or denominators instead of multiplying them.
-
Misunderstanding exponents: Exponents represent repeated multiplication, not repeated addition. (1/2)<sup>3</sup> is not the same as 1/2 + 1/2 + 1/2.
To avoid these misconceptions, practice working with fractions and decimals regularly. Use visual aids, like the cube example described earlier, to solidify your understanding. And don't be afraid to ask questions if you're unsure about something.
FAQ: Frequently Asked Questions
-
What is the value of 1 2 x 1 2 x 1 2? The value is 1/8 or 0.125.
-
How do I convert 1/8 to a decimal? Divide 1 by 8. The result is 0.125.
-
What does (1/2)<sup>3</sup> mean? It means 1/2 multiplied by itself three times: 1/2 x 1/2 x 1/2.
-
Where can I use this knowledge in real life? This knowledge is useful in cooking, baking, probability calculations, scaling recipes, and understanding proportions.
-
Is multiplying by 1/2 the same as dividing by 2? Yes, multiplying by 1/2 is equivalent to dividing by 2.
-
How can I improve my understanding of fractions? Practice working with fractions regularly, use visual aids, and seek help from teachers or online resources.
Conclusion: Mastering the Fundamentals
The seemingly simple expression "1 2 x 1 2 x 1 2" provides a valuable entry point into a world of mathematical concepts and applications. By understanding the basics of fractions, decimals, exponents, and their relationship to volume and probability, we gain a powerful tool for problem-solving and decision-making in various aspects of life. Mastering these fundamental concepts is crucial for continued success in mathematics and for navigating the complexities of the world around us. Embrace the challenge, practice diligently, and unlock the potential hidden within these seemingly simple numbers. The journey of mathematical discovery starts with understanding the basics, and "1 2 x 1 2 x 1 2" is a great place to begin.
Latest Posts
Latest Posts
-
What Does It Mean That Dna Is Antiparallel
Nov 02, 2025
-
What Carries Amino Acids To Ribosomes
Nov 02, 2025
-
How To Multiply Different Size Matrices
Nov 02, 2025
-
Photosynthesis In C4 And Cam Plants
Nov 02, 2025
-
How Does The Digestive System Interact With The Excretory System
Nov 02, 2025
Related Post
Thank you for visiting our website which covers about 1 2 X 1 2 X 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.