1 1 3 On A Number Line
pinupcasinoyukle
Nov 27, 2025 · 8 min read
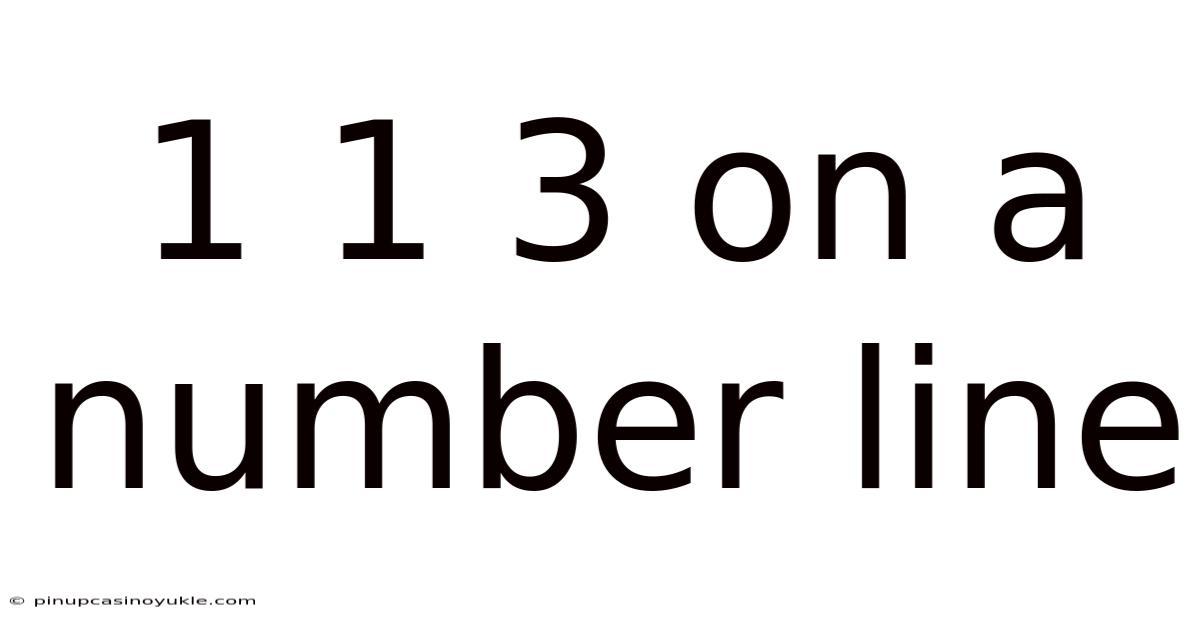
Table of Contents
Let's embark on a journey to understand and represent the number 1 1/3 on a number line, a fundamental skill in grasping numerical concepts. This article will guide you through the process step-by-step, ensuring you understand not only how to plot it, but also why this representation is important. We will cover the basics of number lines, fractions, and mixed numbers before delving into the practical application of locating 1 1/3 accurately.
Understanding the Number Line
The number line is a visual representation of numbers, extending infinitely in both positive and negative directions. It serves as a foundation for understanding numerical order, distance, and operations. Here's what makes it so useful:
- Visual Order: It provides a clear visual of how numbers relate to each other in terms of size. Numbers increase as you move from left to right.
- Distance Representation: The distance between two points on a number line represents the difference between the numbers they represent.
- Foundation for Advanced Concepts: It’s a building block for understanding more complex mathematical concepts like inequalities, functions, and coordinate systems.
Before we can plot 1 1/3, let's ensure we're comfortable with fractions and mixed numbers.
Fractions and Mixed Numbers Refresher
A fraction represents a part of a whole. It consists of two parts:
- Numerator: The number above the fraction bar, indicating how many parts we have.
- Denominator: The number below the fraction bar, indicating the total number of equal parts the whole is divided into.
A mixed number combines a whole number and a fraction. In our case, 1 1/3 is a mixed number, where 1 is the whole number and 1/3 is the fractional part.
Converting Mixed Numbers to Improper Fractions
To better understand and plot mixed numbers on a number line, it's often helpful to convert them into improper fractions. An improper fraction is a fraction where the numerator is greater than or equal to the denominator. Here’s how to convert 1 1/3 to an improper fraction:
- Multiply the whole number by the denominator: 1 * 3 = 3
- Add the numerator to the result: 3 + 1 = 4
- Keep the same denominator: The denominator remains 3.
Therefore, 1 1/3 is equivalent to 4/3. This means we are dealing with four parts, where each part represents one-third of a whole.
Steps to Plot 1 1/3 on a Number Line
Now, let's get practical. Follow these steps to accurately plot 1 1/3 on a number line.
1. Draw and Label the Number Line
- Draw a Straight Line: Use a ruler to draw a straight horizontal line. This line will represent your number line.
- Mark the Origin: Choose a point on the line and label it as 0. This is your origin, the starting point.
- Establish a Scale: Decide on a consistent scale. The distance between consecutive whole numbers should be equal. For example, 1 centimeter or 1 inch between each whole number. Mark and label the whole numbers: 1, 2, 3, and so on, to the right of 0. You can also mark negative numbers to the left of 0, but for our purpose, focusing on positive numbers is sufficient.
2. Locate the Whole Number Part
Our number is 1 1/3. The whole number part is 1. Locate the number 1 on your number line. This is our starting point. We know that 1 1/3 lies between 1 and 2.
3. Divide the Space Between Whole Numbers
The fractional part of our number, 1/3, tells us how to divide the space between the whole numbers. The denominator, 3, indicates that we need to divide the space between 1 and 2 into three equal parts.
- Visual Estimation: Use your eye to estimate where these divisions should be. Try to make the segments as equal as possible.
- Measurement (Optional): For greater precision, measure the distance between 1 and 2. Divide this distance by 3, and then mark the points accordingly. For example, if the distance between 1 and 2 is 3 cm, then each segment will be 1 cm.
4. Mark the Fractional Part
The numerator, 1, tells us which of these divisions to mark. Since we have divided the space between 1 and 2 into three equal parts, and we need to represent 1/3, we will mark the first division after 1. This point represents 1 1/3.
5. Label the Point
Clearly label the point you have marked as 1 1/3 or 4/3. This eliminates any ambiguity and clearly indicates the value represented by that point on the number line.
Example: Plotting 2 3/4 on a Number Line
Let's reinforce the concept with another example: plotting 2 3/4 on a number line.
- Draw and Label: Draw a number line with 0, 1, 2, 3, etc., marked.
- Locate Whole Number: Find 2 on the number line. 2 3/4 lies between 2 and 3.
- Divide the Space: Divide the space between 2 and 3 into four equal parts (because the denominator is 4).
- Mark the Fractional Part: Count three parts from 2 (because the numerator is 3). Mark this point.
- Label: Label the point as 2 3/4.
Tips for Accuracy
- Use a Ruler: Using a ruler ensures that your number line is straight and your divisions are equal.
- Sharp Pencil: A sharp pencil allows for precise marking of points.
- Consistent Scale: Maintain a consistent scale throughout the number line. This is crucial for accurate representation.
- Double-Check: Always double-check your work, especially the division of spaces between whole numbers.
Common Mistakes to Avoid
- Unequal Divisions: Dividing the space between whole numbers into unequal parts is a common error. Use a ruler or careful estimation to avoid this.
- Miscounting: Miscounting the fractional parts can lead to an incorrect placement. Double-check your counting.
- Ignoring the Whole Number: Forgetting to account for the whole number part and only focusing on the fraction will result in plotting the number in the wrong interval.
- Inconsistent Scale: Using different scales on the same number line will distort the representation and lead to inaccuracies.
Why is This Important?
Representing numbers, including fractions and mixed numbers, on a number line is a fundamental skill with several important applications:
- Conceptual Understanding: It reinforces the understanding of numerical order and the relative magnitude of numbers.
- Problem-Solving: It aids in solving problems involving comparison, addition, and subtraction of numbers.
- Visual Aid: It provides a visual aid for understanding mathematical concepts, making them more accessible, especially for visual learners.
- Foundation for Higher Math: It lays the groundwork for understanding more advanced concepts in algebra, geometry, and calculus.
Real-World Applications
The ability to visualize numbers on a number line translates to various real-world scenarios:
- Measurement: Imagine measuring fabric for a sewing project. You might need to work with fractions of an inch, and visualizing these on a mental number line helps in precise cutting.
- Cooking: Recipes often involve fractional measurements of ingredients. A number line can help visualize the proportions and ensure accurate cooking.
- Construction: Construction workers use number lines (often in the form of measuring tapes) to precisely measure lengths and distances.
- Finance: Understanding interest rates and financial growth can be visualized using a number line, helping to understand the compounding effect.
Going Beyond: Number Lines and Negative Numbers
While we focused on positive numbers and fractions, remember that number lines extend infinitely in both directions. Let's briefly touch upon how negative numbers fit into the picture.
Negative numbers are located to the left of zero on the number line. The further a negative number is from zero, the smaller its value. For instance, -3 is smaller than -1.
You can plot negative fractions and mixed numbers on a number line using the same principles we discussed earlier, but remember to move to the left of zero. For example, -1 1/2 would be located halfway between -1 and -2.
Advanced Applications of Number Lines
Beyond basic plotting, number lines can be used to illustrate more complex mathematical operations:
- Addition: To add two numbers on a number line, start at the first number and move to the right by the value of the second number.
- Subtraction: To subtract two numbers, start at the first number and move to the left by the value of the second number.
- Multiplication: Multiplication can be visualized as repeated addition. For example, 3 x 2 can be seen as starting at 0 and moving 2 units to the right three times.
- Inequalities: Number lines are excellent for representing inequalities. For example, x > 2 can be shown by shading the portion of the number line to the right of 2 (with an open circle at 2 to indicate that 2 is not included).
Conclusion
Plotting numbers, including fractions and mixed numbers like 1 1/3, on a number line is a fundamental skill that builds a strong foundation for understanding numerical relationships and mathematical concepts. By following the steps outlined in this guide, practicing regularly, and avoiding common mistakes, you can master this skill and unlock a deeper appreciation for the beauty and logic of mathematics. The number line is more than just a line with numbers; it's a powerful tool for visualizing and understanding the world around us.
Latest Posts
Latest Posts
-
What Stage Do Sister Chromatids Separate
Nov 27, 2025
-
How To Find Profit Maximizing Quantity
Nov 27, 2025
-
What Was A Major Weakness Of The Articles Of Confederation
Nov 27, 2025
-
Electron Affinity Trend In Periodic Table
Nov 27, 2025
-
For Each Function State Whether It Is Linear
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about 1 1 3 On A Number Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.